黑龙江省鹤岗市第一中学2020届高三上学期10月月考数学(文)试题
2017级高三第一次月考文科数学试题
一、选择题(共12题,每题5分)
1.已知全集 ,集合 ,,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】
先求出集合A的补集,进而进行并运算即可.
【详解】∵全集 ,集合 ,
∴,又
∴
故选:D
【点睛】本题考查集合的交并补运算,理解好题意是解题的关键,属于基础题.
2.复数( )
A. B. C. D.
【答案】D
【解析】
试题分析:,选D.
考点:复数的四则运算.
3.下列正确的是( )
A. 若a,b∈R,则
B. 若x<0,则x+≥-2=-4
C. 若ab≠0,则
D. 若x<0,则2x+2-x>2
【答案】D
【解析】
对于A,当ab<0时不成立;对于B,若x<0,则x+=- ≤-2 =-4,当且仅当x=-2时,等号成立,因此B选项不成立;对于C,取a=-1,b=-2,+=-
2成立.
故选D.
4.已知,,,则( )
A. B. C. D.
【答案】B
【解析】
【分析】
由∈(0,1),b=lnln2<0,,即可得出大小关系.
【详解】∈(0,1),b=lnln2<0,
∴b<a<c.
故选:B.
【点睛】本题考查了指数与对数运算性质及其指数对数函数的单调性,考查了推理能力与计算能力,属于基础题.
5.已知与均为单位向量,它们的夹角为,那么等于( )
A. B. C. D. 4
【答案】A
【解析】
本题主要考查的是向量的求模公式。由条件可知==,所以应选A。
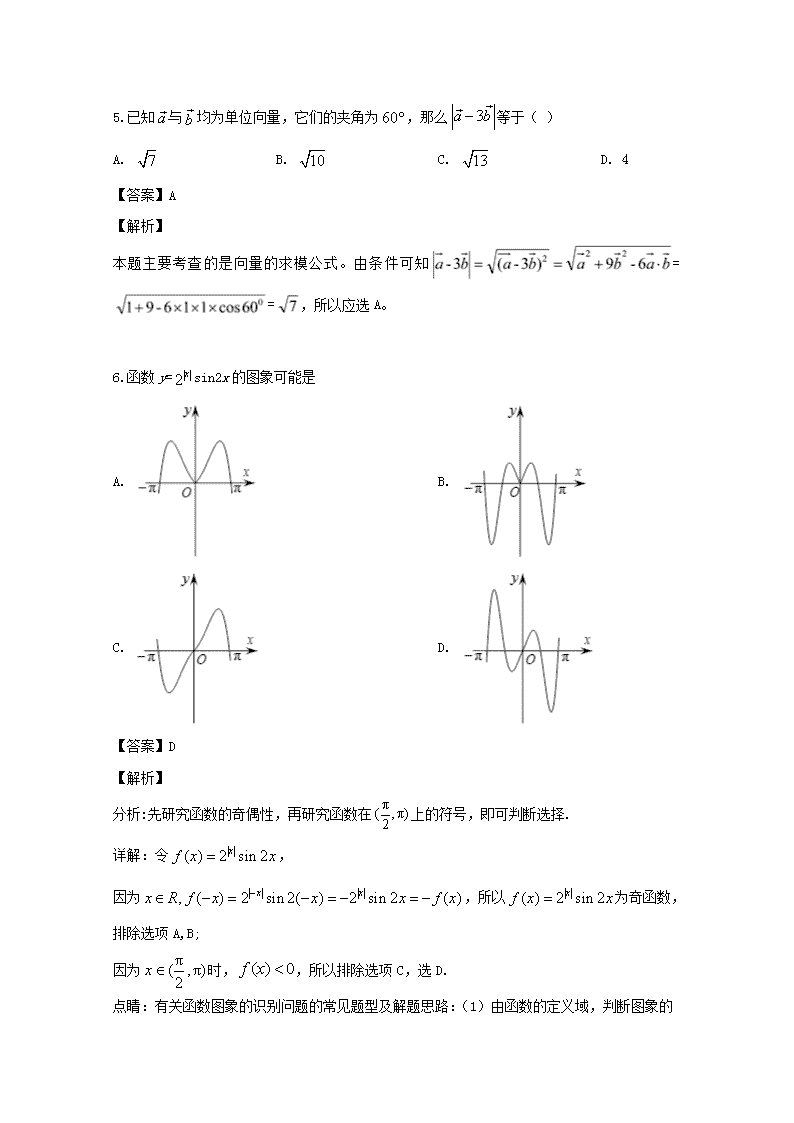
6.函数y=sin2x的图象可能是
A. B.
C. D.
【答案】D
【解析】
分析:先研究函数的奇偶性,再研究函数在上的符号,即可判断选择.
详解:令,
因为,所以为奇函数,排除选项A,B;
因为时,,所以排除选项C,选D.
点睛:有关函数图象的识别问题的常见题型及解题思路:(1)由函数的定义域,判断图象的左、右位置,由函数的值域,判断图象的上、下位置;(2)由函数的单调性,判断图象的变化趋势;(3)由函数的奇偶性,判断图象的对称性;(4)由函数的周期性,判断图象的循环往复.
7.已知函数,则为 ( )
A. 是奇函数,且在上是增函数 B. 是偶函数,且在上是增函数
C. 是奇函数,且在上是减函数 D. 是偶函数,且在上是减函数
【答案】A
【解析】
【分析】
根据指数函数的图象与性质,结合奇偶性和单调性的性质进行判断即可.
详解】解:∵f(﹣x)=2﹣x﹣2x=﹣(2x﹣2﹣x)=﹣f(x),
∴f(x)是奇函数,
∵y=2x增函数y=2﹣x是减函数,
∴y=2x﹣2﹣x是增函数,
故选:A.
【点睛】本题主要考查函数奇偶性和单调性的判断,利用奇偶性的定义以及单调性的性质进行判断是解决本题的关键.
8.等差数列中,,则( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据等差中项的性质,,,再将转化为含有的算式即可.
【详解】因为数列为等差数列,
所以,,
则,
故选:B.
【点睛】本题考查了等差数列的性质,等差中项,等差数列的前项和.属于基础题.
9.在中,分别为内角的对边,若,则( )
A. B. 或 C. D. 或
【答案】A
【解析】
【分析】
根据题意,有的值求出的值,结合正弦定理可得,计算可得的值,比较、的大小,分析可得答案.
【详解】根据题意,在中,,则,且为锐角;
又由,可得,
又由,则,则,
故选:A.
【点睛】本题考查三角形中正弦定理的应用,关键是掌握正弦定理的形式,属于基础题.
10.设均为不等于的正实数,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】
首先通过对数运算可判断出时,,得到充分条件成立;当
时,可根据对数运算求出或或,得到必要条件不成立,从而可得结果.
【详解】由,可得:,则,即
可知“”是“”的充分条件
由可知,则
或
或或
可知“”是“”的不必要条件
综上所述:“”是“”的充分不必要条件
本题正确选项:
【点睛】本题考查充分条件、必要条件的判断,关键是能够通过对数运算来进行判断.
11.已知定义在上的奇函数满足,当时,,则( )
A. 2019 B. 1 C. 0 D. -1
【答案】C
【解析】
【分析】
根据题意推导出函数的对称性和周期性,可得出该函数的周期为,于是得出
可得出答案。
【详解】函数是上的奇函数,则,
,所以,函数的周期为,
且,,,
,,
,
,故选:C。
【点睛】本题考查抽象函数求值问题,求值要结合题中基本性质和相应的等式进行推导出其他性质,对于自变量较大的函数值的求解,需要利用函数的周期性进行求解,考查逻辑推理能力与计算能力,属于中等题。
12.已知函数在上可导且满足,则下列一定成立的为( )
A. B. C. D.
【答案】A
【解析】
【分析】
构造函数,利用导数判断函数在上的单调性,可得出与的大小关系,经过化简可得出正确选项.
【详解】构造函数,则,当时,.
所以,函数在上单调递增,,,即,
即,故选:A.
【点睛】本题考查函数单调性的应用,根据导数不等式的结构构造新函数求解是解本题的关键,考查分析问题和解决问题的能力,属于中等题.
二、填空题(共4题,每题5分)
13.已知实数满足约束条件,则的最大值为_______.
【答案】8
【解析】
【分析】
①画可行域②z为目标函数纵截距四倍③画直线0=2x+4y,平移直线过(0,2)时z有最大值
【详解】解:画可行域如图,z为目标函数纵截距四倍,画直线0=2x+4y,平移直线过(0,2)点时z有最大值8
故答案为8
【点睛】本题考查简单线性规划,解题的重点是作出正确的约束条件对应的区域,根据目标函数的形式及图象作出正确判断找出最优解.
14.已知函数.,则曲线在点处的切线方程为________.
【答案】
【解析】
【分析】
求得f(x)的导数,可令x=2
,可得切线的斜率,以及切点,再由点斜式方程可得切线方程.
【详解】由题意可得:,
∴
∴切线斜率为1,切点坐标为:,
由点斜式可得切线方程:
即.
故答案为:
【点睛】本题考查导数的运用:求切线方程,考查直线方程的运用,属于基础题.
15.在中,角,,的对边分别为,,,且,,则角等于__________.
【答案】
【解析】
,所以,
则。
点睛:本题考查余弦定理在解三角形中的应用。本题条件为一个角,边的二次关系,则利用余弦定理解三角形。本题中,通过余弦定理,得到,求得角C。解三角形题型关键是正确应用正弦定理和余弦定理。
16. 观察下列等式:
据此规律,第个等式可写为 ________.
【答案】
【解析】
试题分析:由已知得,第个等式含有项,其中奇数项为,偶数项为,其等式右边为后项的绝对值之和,所以第个等式为.
考点:归纳推理.
三、解答题(17、18、19、20、21每题12分,22、23每题10分)
17.已知函数
(I)求的值
(II)求的最小正周期及单调递增区间.
【答案】(I)2;(II)最小正周期是,.
【解析】
【分析】
(Ⅰ)直接利用三角函数关系式的恒等变换,把函数的关系式变形成正弦型函数,进一步求出函数的值.
(Ⅱ)直接利用函数的关系式,求出函数的周期和单调区间.
详解】(Ⅰ)f(x)=sin2x﹣cos2xsin x cos x,
=﹣cos2xsin2x,
=﹣2,
则f()=﹣2sin()=2,
(Ⅱ)因为.
所以的最小正周期是.
由正弦函数的性质得
,
解得,
所以,的单调递增区间是.
【点睛】本题主要考查了三角函数的化简,以及函数的性质,是高考中的常考知识点,属于基础题,强调基础的重要性;三角函数解答题中,涉及到周期,单调性,单调区间以及最值等考点时,都属于考查三角函数的性质,首先应把它化为三角函数的基本形式即,然后利用三角函数的性质求解.
18.已知公差不为0的等差数列的前三项和为12,且成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
【答案】(1);(2)
【解析】
【分析】
(1)设等差数列的首项为,公差为,由题意列出方程组,求得,即可得到数列的通项公式.
(2)由(1)知,利用等比数列的前项和公式,即可求解数列的和.
因为,所以数列是以4为首项,4为公比等比数列,
【详解】(1)设等差数列的首项为,公差为.
依题意有,即.
由,解得,所以.
(2)由(1)知.
因为,所以数列是以4为首项,4为公比的等比数列,
所以.
【点睛】等差、等比数列的综合是高考考查的热点,一般都是突出基本量和方程思想,强调基本的运算.解题时,关键在于用好它们的有关知识,理顺两个数列间的关系.注意运用等差数列与等比数列的基本量,即与来表示数列中的所有项,还应注意等差数列与等比数列之间的相互转化.
19.已知的内角,,所对的边分别为,,,且.
(Ⅰ)求角的大小;
(Ⅱ)若,,求的值.
【答案】(1)(2)2+.
【解析】
(Ⅰ)由,得,
即,∴,故.
(Ⅱ)由,得,即,①
又,∴,②
由①②可得,所以.
【点睛】利用正、余弦定理进行“边转角”或“角转边”是近几年高考的热点,常求三角形的边、角及三角形的面积.要灵活运用正弦定理进行“边转角”或“角转边”,结合余弦定理和面积公式,注意运用 三者的关系解题.
20.已知数列中,且.
(Ⅰ)求,;并证明是等比数列;
(Ⅱ)设,求数列的前项和.
【答案】(Ⅰ),证明见解析;(Ⅱ).
【解析】
【分析】
(Ⅰ)根据递推式逐步代入算出和的值,再根据题意将的递推式代入进行计算化简最终会得到和的关系,最终得证数列是等比数列;(Ⅱ)先根据(Ⅰ)求得的通项公式,得到,由通项公式的特点可根据错位相减法得到数列的前项和.
【详解】(Ⅰ)由题意,可知:
,
.
①当时,,
②当时, .
数列是以为首项,为公比的等比数列.
(Ⅱ)由(Ⅰ),可知:
,
..
.
, ③
④
③-④,可得:
,
【点睛】本题第(Ⅰ)题主要考查根据递推公式逐步代值,以及根据递推公式求出通项公式;第(Ⅱ)题主要考查利用错位相减法来求数列的前项和.本题属中档题.
21.已知函数.
(1)若,求函数的单调区间;
(2)对任意的,不等式恒成立,求实数的取值范围.
【答案】(1)单调递增区间为,单调递减区间为;(2).
【解析】
【分析】
(1)求出函数的定义域与导数,然后在定义域内分别解不等式和,可得出函数的单调递减区间和单调递增区间;
(2)由,利用参变量分离法得出在恒成立,令,将问题转化为,然后利用导数求出函数在
上的最小值,可得出实数的取值范围.
【详解】(1)当时,,定义域为,.
令,得;令,得.
因此,函数的单调递增区间为,单调递减区间为;
(2)不等式恒成立,等价于在恒成立,
令,,则,
令,,.
所以在单调递增,而,
所以时,,即,单调递减;
时,,即,单调递增.
所以在处取得最小值,
所以,即实数的取值范围是.
【点睛】本题考查利用导数求函数的单调区间,以及利用导数研究不等式恒成立问题,解题的关键在于利用参变量分离转化为函数的最值来求解,避免了分类讨论,考查化归与转化思想,属于中等题.
选修4-4:坐标系与参数方程
22.以平面直角坐标系的坐标原点为极点,以轴的非负半轴为极轴,以平面直角坐标系的长度为长度单位建立极坐标系. 已知直线的参数方程为 (为参数),曲线的极坐标方程为 .
(1)求曲线 的直角坐标方程;
(2)设直线与曲线相交于两点,求.
【答案】(1)(2)
【解析】
【试题分析】(1)借助极坐标与直角坐标之间的互化关系进行求解;(2)先将直线的参数方程代入抛物线方程中,借助根与系数的关系及直线方程中的参数的几何意义求弦长:
解:
(1)由,既 曲线的直角坐标方程为.
(2) 的参数方程为代入,整理的,所以,
所以.
选修4-5:不等式选讲
23.已知函数
(Ⅰ)若,,求不等式的解集;
(Ⅱ)若,,且,求证:.
【答案】(Ⅰ);(Ⅱ)证明见解析.
【解析】
【分析】
(Ⅰ)利用分类讨论法解不等式求不等式的解集;(Ⅱ)先用绝对值不等式的性质求得,再根据基本不等式可得,利用不等式的传递性可得.
【详解】(Ⅰ)时,或或,
解得,
故不等式的解集为;
(Ⅱ)时,当且仅当时,取等.
∵,∴,
当且仅当时取等.
故.
【点睛】本题考查了绝对值不等式的解法,考查了三角绝对值不等式的应用,考查了基本不等式求最值,属中档题.