- 2021-04-14 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年山西省榆社中学高二下学期期中考试数学(文)试题 Word版
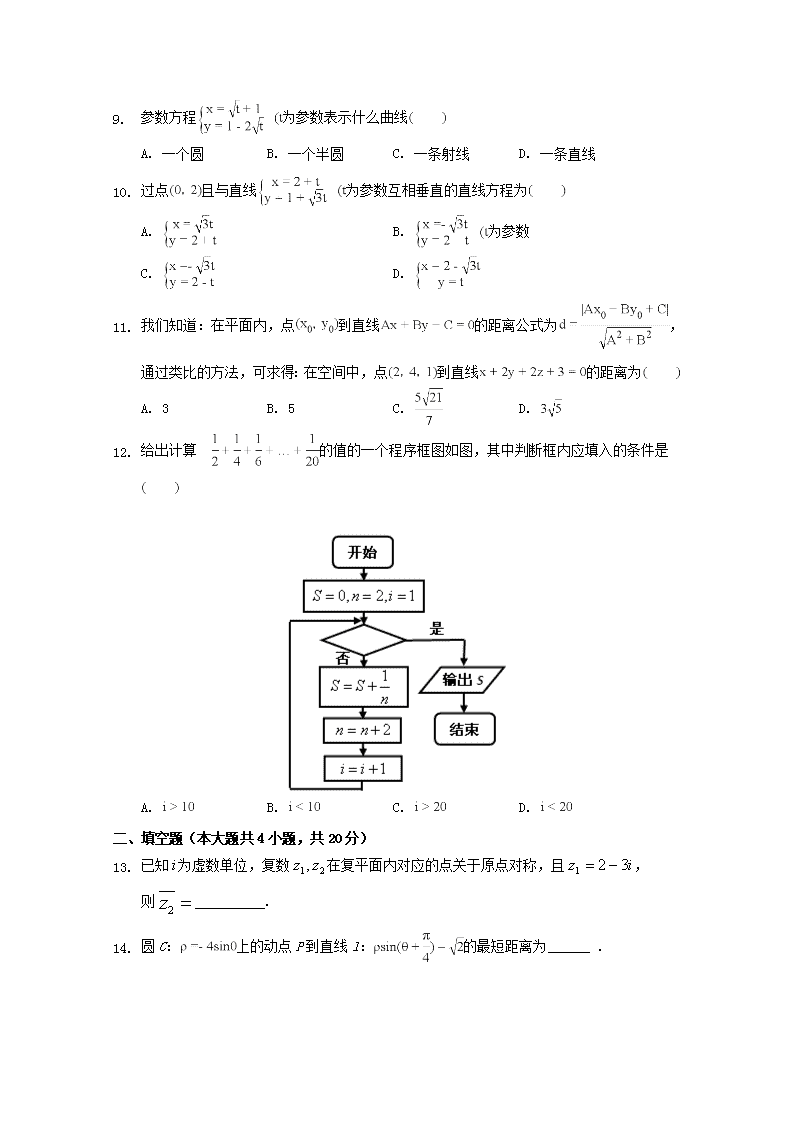
榆社中学2017—2018学年度第二学期期中考试 高二数学(文)试题 2018.5 一、选择题(本大题共12小题,共60分) 1. 设i为虚数单位,,“复数是纯虚数”是“”的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件 2. 用三段论推理:“任何实数的绝对值大于0,因为a是实数,所以a的绝对值大于0”,你认为这个推理 A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 是正确的 3. 设复数,则在复平面内对应的点位于 A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 4. 点M的直角坐标是,则点M的极坐标为 A. B. C. D. 5. 已知的取值如下表: 0 1 3 4 2.2 4.3 4.8 6.7 与线性相关,且线性回归直线方程为,则= A. B. C. D. 6. 直线和圆的位置关系是 A. 相切 B. 相离 C. 相交但不过圆心 D. 相交且过圆心 7. 若直线l的参数方程为为参数,则直线l的倾斜角的余弦值为 A. B. C. D. 8. 直线为参数 被圆截得的弦长等于 A. B. C. D. 1. 参数方程为参数表示什么曲线 A. 一个圆 B. 一个半圆 C. 一条射线 D. 一条直线 2. 过点且与直线为参数互相垂直的直线方程为 A. B. 为参数 C. D. 3. 我们知道:在平面内,点到直线的距离公式为,通过类比的方法,可求得:在空间中,点到直线的距离为 A. 3 B. 5 C. D. 4. 给出计算 的值的一个程序框图如图,其中判断框内应填入的条件是 A. B. C. D. 二、填空题(本大题共4小题,共20分) 5. 已知为虚数单位,复数在复平面内对应的点关于原点对称,且, 则 . 6. 圆C:上的动点P到直线l:的最短距离为______ . 1. 已知F是曲线为参数的焦点,则定点与F点之间的距离______. 2. “开心辞典”中有这样个问题:给出一组数,要你根据规律填出后面的第几个数,现给出一组数:,它的第8个数可以是______ . 三、解答题(本大题共6小题,共70分) 17.已知z为复数,和均为实数,其中i是虚数单位. 求复数z和; 若在第四象限,求实数m的取值范围. 18.某种产品的广告费用支出万元与销售额万元之间有如下的对应数据: x 2 4 5 6 8 y 30 40 60 50 70 求回归直线方程; 据此估计广告费用为12万元时的销售额约为多少? 参考公式:. 19.通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下列联表: 男生 女生 合计 挑同桌 30 40 70 不挑同桌 20 10 30 总计 50 50 100 Ⅰ从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;Ⅱ根据以上列联表,是否有以上的把握认为“性别与在选择座位时是否挑同桌”有关? 下面的临界值表供参考: 参考公式:,其中 20.在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为,直线l的参数方程为,直线l和圆C交于两点,P是圆C上不同于的任意一点 求圆C的直角坐标方程; 求面积的最大值. 21.已知等式:;; ;由此可归纳出对任意角度都成立的一个等式,并予以证明. 22.已知曲线的参数方程为为参数在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线:.Ⅰ求曲线的普通方程和的直角坐标方程;Ⅱ若与相交于A、B两点,设点,求的值. 查看更多