- 2021-04-14 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习平面向量的基本定理和坐标表示课件(全国通用)
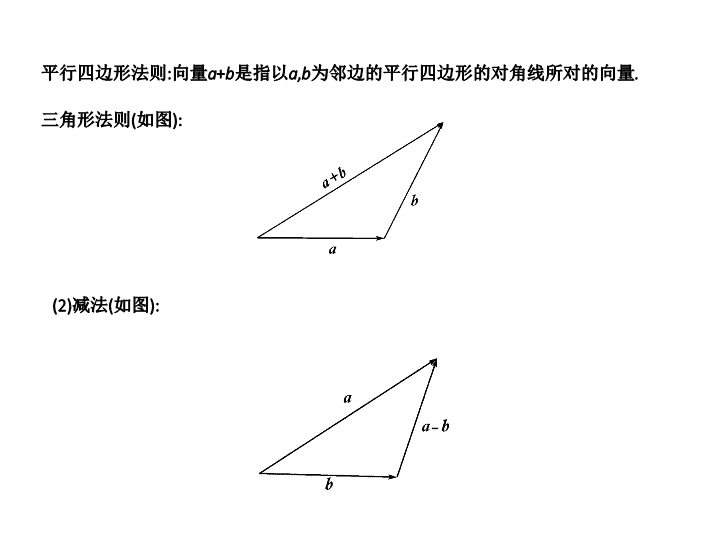
第五章 平面向量 1 . 向量的概念 : 既有 大小 又有 方向 的量叫做向量 , 向量的大小叫做向量的长度 ( 或称模 ) . 2 . 向量的运算 ( 几何意义 ): (1) 加法 : 第 1 节 平面向量的基本定理 和坐标表示 平行四边形法则 : 向量 a + b 是指以 a , b 为邻边的平行四边形的对角线所对的向量 . 三角形法则 ( 如图 ): (2) 减法 ( 如图 ): 【 例 1】 (2014 南海质检 ) 已知向量 a =(1, m ), b =( m ,2), 若 a ∥ b , 则实数 m 等于 ( ) 【 例 2 】 (2013 全国新课标 (Ⅱ)) 已知正方形 ABCD 的边长为 2,E 为 CD 的中点 , 【 答案 】 2 【 解析 1】 ( 坐标法 ) 以 A 为原点 , AB , AD 为 x , y 轴建立直角坐标系 , 则 : 【 例 3】 (2016 高考新课标 Ⅱ 理数 ) 已知向量 a =(1, m ), b =(3, - 2), 且 ( a + b )⊥ b , 则 m = ( ) A. - 8 B.-6 C.6 D.8 【 答案 】 D 【 解析 】 向量 a + b =(4, m- 2), 由 ( a + b )⊥ b 得 4×3+( m- 2)×( - 2)=0, 解得 m= 8, 故选 D . 【 例 4】 (2017 高考新课标 Ⅰ 文 ) 已知向量 a =( - 1,2), b =( m ,1) . 若向量 a + b 与 a 垂直 , 则 m = . 【 答案 】 7 【 解析 】 由题得 a + b= ( m- 1,3), 因为 ( a+b )· a= 0, 所以 - ( m- 1)+2×3=0, 解得 m =7 . 1 . (2015 深圳二模 ) 平面向量 a= (1,-2), b =( - 2, n ), 若 a ∥ b , 则 n 等于 ( ) A.4 B. - 4 C. - 1 D.2 【 答案 】 A 【 解析 】 因为 a ∥ b , 所以有 1× n- ( - 2)×( - 2)=0, 解得 n= 4 . 选 A . 2 . (2014 广东高考 ) 已知 a= (1,2), b= (3,1), 则 b-a = ( ) A.( - 1,2) B.(2, - 1) C.(2,0) D.(4,3) 【 答案 】 B 【 解析 】 b-a =(3 - 1,1 - 2)=(2, - 1) . 选 B . 3 . (2017 新课标 Ⅲ) 已知向量 a =( - 2,3), b =(3, m ) 且 a ⊥ b , 则 m = . 【 答案 】 2 【 解析 】 由题意可得 :-2×3+3m=0,∴m=2. 4 . (2016 新课标 Ⅱ 理 ) 已知 z =( m +3)+( m- 1) i 在复平面内对应的点在第四象限 , 则实数 m 的取值范围是 ( ) A.( - 3,1) B.( - 1,3) C.(1,+∞) D.(-∞, - 3) 5 . 已知向量 p =(2,-3), q =( x ,6) 且 p ∥ q , 则 | p+q | 的值为 ( ) 10 . (2013 全国卷高考文科 ) 已知向量 m =( λ +1,1), n= ( λ +2,2), 若 ( m + n )⊥( m-n ), 则 λ = ( ) A.-3 B.-4 C.-2 D. - 1 【 答案 】 A 【 解析 】 m + n= (2 λ +3,3), m-n= ( - 1, - 1), 当 ( m + n )⊥( m-n ) 时 , 有 (2 λ +3,3)·( - 1, - 1) = 0,∴(2 λ +3)·( - 1)+3×( - 1) = 0, 解得 λ=- 3, 选 A . 11 . (2016 北京高考 ) 设 a , b 是向量 , 则“ | a |=| b |” 是“ | a + b |=| a - b |” 的 ( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 【 答案 】 D 【 解析 】 由 | a + b |=| a-b |⇔( a + b ) 2 =( a-b ) 2 ⇔ a · b =0⇔ a ⊥ b , 故是既不充分也不必要条件 , 故选 D . 14 . 设向量 a =(cos α ,sin α ), b =(cos β ,sin β ), 其中 0< α < β < π , 若 |2 a + b |=| a- 2 b |, 则 β-α = .查看更多