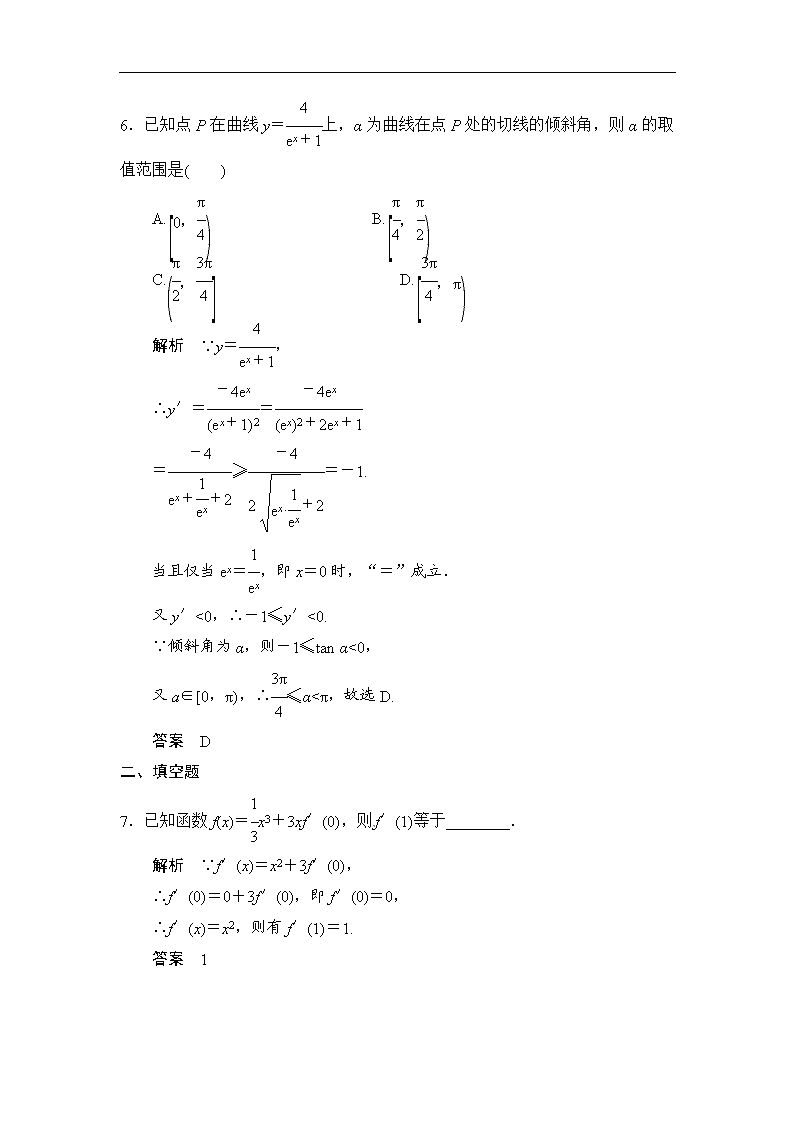高考数学复习专题练习第1讲 变化率与导数、导数的运算
第三章 导数及其应用
第1讲 变化率与导数、导数的运算
一、选择题
1.下列函数求导运算正确的个数为( )
①(3x)′=3xlog3e;②(log2x)′=;③(ex)′=ex;
④′=x;⑤(x·ex)′=ex+1.
A.1 B.2
C.3 D.4
解析 求导运算正确的有②③2个,故选B.
答案 B[来源:学|科|网]
2.函数f(x)=mx3+(m+1)x2+x+2,若f′(1)=18,则m=( )
A.4 B.3
C.5 D.6
解析 ∵f′(x)=3mx2+2(m+1)x+1,
∴f′(1)=3m+2m+2+1=18,
∴m=3.
答案 B
3.已知函数f(x)=x3+2ax2+x(a>0),则f(2)的最小值为
( ).
A.12 B.12+8a+
C.8+8a+ D.16
解析 f(2)=8+8a+,令g(a)=8+8a+,则g′(a)=8-,由g′(a)>0得a>
,由g′(a)<0得0
0)的导数为________.
解析 对y=x(x>0)两边取对数得lny=lnx,两边求导得=,∴y′=x.=x-2(1-ln x).
答案 y′=x-2(1-ln x)
三、解答题
11.求下列函数的导数:
(1)y=(2x+1)n(n∈N+); (2)y=ln (x+);
(3)y=2xsin(2x+5).
解 (1)y′=n(2x+1)n-1·(2x+1)′=2n(2x+1)n-1.
(2)y′=·=.
(3)y′=2sin(2x+5)+4xcos(2x+5).
12.已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线的方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;
(3)如果曲线y=f(x)的某一切线与直线y=-x
+3垂直,求切点坐标与切线的方程.
解 (1)可判定点(2,-6)在曲线y=f(x)上.
∵f′(x)=(x3+x-16)′=3x2+1.
∴f′(x)在点(2,-6)处的切线的斜率为k=f′(2)=13.
∴切线的方程为y=13(x-2)+(-6),
即y=13x-32.
(2)法一 设切点为(x0,y0),
则直线l的斜率为f′(x0)=3x+1,
∴直线l的方程为y=(3x+1)(x-x0)+x+x0-16,
又∵直线l过点(0,0),∴0=(3x+1)(-x0)+x+x0-16,
整理得,x=-8,∴x0=-2,
∴y0=(-2)3+(-2)-16=-26,k=3×(-2)2+1=13.
∴直线l的方程为y=13x,切点坐标为(-2,-26.)
法二 设直线l的方程为y=kx,切点为(x0,y0),
则k==
又∵k=f′(x0)=3x+1,∴=3x+1,
解之得x0=-2,
∴y0=(-2)3+(-2)-16=-26,k=3×(-2)2+1=13.
∴直线l的方程为y=13x,切点坐标为(-2,-26).
(3)∵切线与直线y=-x+3垂直,
∴切线的斜率k=4.
设切点的坐标为(x0,y0),则f′(x0)=3x+1=4,
∴x0=±1,
∴或
切线方程为y=4(x-1)-14或y=4(x+1)-18.
即y=4x-18或y=4x-14.
13.设函数f(x)=ax-,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y
-12=0.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
(1)解 方程7x-4y-12=0可化为y=x-3,
当x=2时,y=.又f′(x)=a+,
于是解得故f(x)=x-.
(2)证明 设P(x0,y0)为曲线上任一点,由f′(x)=1+知,曲线在点P(x0,y0)处的切线方程为y-y0=·(x-x0),即y-=(x-x0).
令x=0得,y=-,从而得切线与直线x=0交点坐标为.
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0).
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为|2x0|=6.
故曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,此定值为6.
14.已知曲线Cn:y=nx2,点Pn(xn,yn)(xn>0,yn>0)是曲线Cn上的点(n=1,2,…).
(1)试写出曲线Cn在点Pn处的切线ln的方程,并求出ln与y轴的交点Qn的坐标;
(2)若原点O(0,0)到ln的距离与线段PnQn的长度之比取得最大值,试求点Pn的坐标(xn,yn).
解 (1)∵y′=2nx,∴y′|x=xn=2nxn,切线ln的方程为:y-n·x=2nxn(x-xn).
即:2nxn·x-y-n·x=0,令x=0,
得y=-nx,∴Qn(0,-nx).
(2)设原点到ln的距离为d,则
d==,
|PnQn|=.
所以=≤=,
当且仅当1=4n2x,即x=(xn>0)时,等号成立,
此时,xn=,所以,Pn.