- 2021-04-14 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
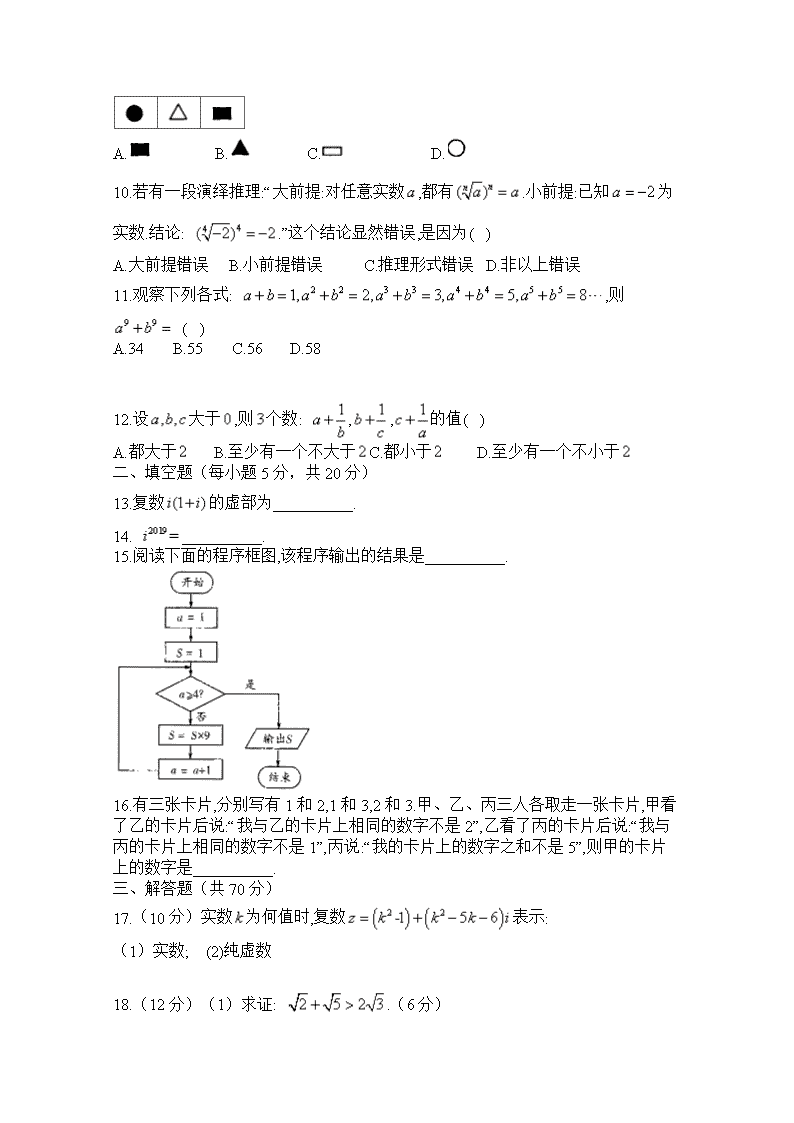
河南省开封市第十中学2018-2019高二第二学期月考数学(文)试卷
高二下学期月考试卷(文科数学) 参考公式:1、回归方程中, , 2、独立性检验: 0.4 0.25 0.15 0.10 0.05 0.025 0.01 0.005 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 一、选择题(每小题5分,共60分) 1.某中学男生1250名中有420名近视,女生1210名中有370名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力( ) A.回归分析 B.排列与组合 C.独立性检验 D.概率 2.下面是调查某地区男女中学生喜欢理科的等高条形图,阴影部分表示喜欢理科的百分比,从图可以看出( ) A.性别与喜欢理科无关 B.女生中喜欢理科的比为 C.男生比女生喜欢理科的可能性小些 D.男生喜欢理科的比约为 3.已知变量与正相关,且由观测数据算得样本平均数,,则由该观测数据算得的线性回归方程可能为( ) A. B. C. D. 4.下列是一个列联表总计 总计 总计 则表中处的值分别为( ) A.94、96 B.52、50 C.52、54 D.54、52 5.在一线性回归模型中,计算相关指数,下列哪种说法不够妥当?( ) A.该线性回归方程的拟合效果较好 B.解释变量对于预报变量变化的贡献率一定为 C.随机误差对预报变量的影响约占 D.此模型的预报精度较高 6.用反证法证明命题“设,为实数,则方程至少有一个实根”时,要做的假设是( ) A.方程没有实根 B.方程至多有一个实根 C.方程至多有两个实根 D.方程恰好有两个实根 7.复数 (为虚数单位)在复平面内对应的点所在象限为( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 8.下列结构图中要素之间表示从属关系的是( ) A. B. C. D. 9.观察图形规律,在其右下角的空格内画上合适的图形为( ) A. B. C. D. 10.若有一段演绎推理:“大前提:对任意实数,都有.小前提:已知为实数.结论: .”这个结论显然错误,是因为( ) A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误 11.观察下列各式: ,则 ( ) A.34 B.55 C.56 D.58 12.设大于,则个数: ,,的值( ) A.都大于 B.至少有一个不大于C.都小于 D.至少有一个不小于 二、填空题(每小题5分,共20分) 13.复数的虚部为__________. 14. __________. 15.阅读下面的程序框图,该程序输出的结果是__________. 16.有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是__________. 三、解答题(共70分) 17.(10分)实数为何值时,复数表示: (1)实数; (2)纯虚数 18.(12分)(1)求证: .(6分) (2)已知:,求证:中至少有一个数大于10.(6分) 19.(12分)已知复数. (1)求复数(6分) (2)若,求实数的值.(6分) 20.(12分)随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表: 年份 2010 2011 2012 2013 2014 时间代号 1 2 3 4 5 储蓄存款 (千亿元) 5 6 7 8 9 (1)求关于的回归方程.(8分) (2)用所求回归方程预测该地区年的人民币储蓄存款.(4分) 21.(12分)某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示: 喜欢甜品 不喜欢甜品 合计 南方学生 60 20 80 北方学生 10 10 20 合计 70 30 100 (1)(6分)根据表中数据,问是否有的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”; (2)(6分)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率. 22.(12分)某同学发现,下面四个式子的结果都等于同一个常数: ①; ②; ③; ④ (1)请从中选一个式子求出这个常数,并推广到一般形式(5分) (2)请证明你的猜想.(7分) 参考答案 一、选择题 2.答案:C 解析:由题图可知,女生中喜欢理科的百分比约为,男生中喜欢理科的百分比约为%,因此男生比女生喜欢理科的可能性大些. 3.答案:A 解析:变量与正相关,可以排除C,D;样本平均数代入可求这组样本数据的回归直线方程. ∵变量与正相关, ∴可以排除C,D; 样本平均数,,代入A符合,B不符合, 故选:A. 4.答案:C 解析: 5.答案:D 解析:由相关指数的意义可知,A,B,C说法均妥当.相关指数,其值较大,说明残差平方和较小,绝大部分样本点分布在回归直线附近,不一定有的样本点在回归直线上. 6.答案:A 解析:“方程至少有一个实根”等价于“方程有一个实根或两个实根”所以该命题的否定是“方程没有实根”.故选A. 7.答案:D 解析:,它在复平面内对应的点为,在第四象限.故选D. 8.答案:C 解析: 9.答案:A 解析:图形涉及○、△、 三种符号,其中△与○各有3个,且各自有两黑一白,所以缺一个黑色符号 10.答案:A 解析:选A.因为为偶数时,若有意义,则.故大前提错误. 11.答案:D 解析:,,,. 12.答案:D 解析: 假设都小于 则 ∴,① 又大于 所以. ∴.② 故①与②式矛盾,假设不成立 所以至少有一个不小于. 二、填空题 答案:73.5 解析:由题表可知, ,, 代入回归方程,得, 所以回归方程为, 所以当时, (万元). .答案:1和3 解析:丙说他的卡片上的数字之和不是5,所以丙的卡片上的数字要么是1和2,要么是1和3.又乙说他与丙的卡片上相同的数字不是1,所以卡片2和3必定在乙手中.因为甲与乙的卡片上相同的数字不是2,所以甲的卡片上的数字只能是1和3. 三、解答题 17.答案:1.当,即或时, 是实数. 2.当即时, 是纯虚数. 21.答案:1. 列表计算如下: 1 1 5 1 5 2 2 6 4 12 3 3 7 9 21 4 4 8 16 32 5 5 10 25 50 15 36 55 120 这里.,,又,从而,故所求回归方程为. 2.将代入回归方程可预测该地区2015年的人民币储蓄存款为 (千亿元). 解析: 22.答案:1. 查看更多