2018年达利教育卓越奖初中学科竞赛八年级数学

2018年达利教育卓越奖初中学科竞赛八年级数学

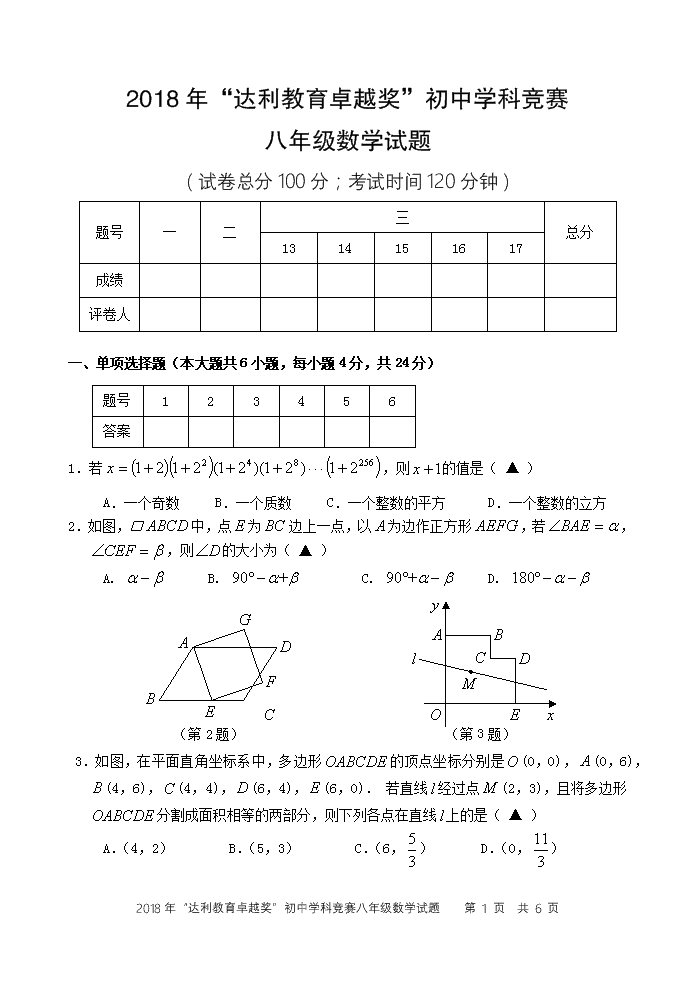
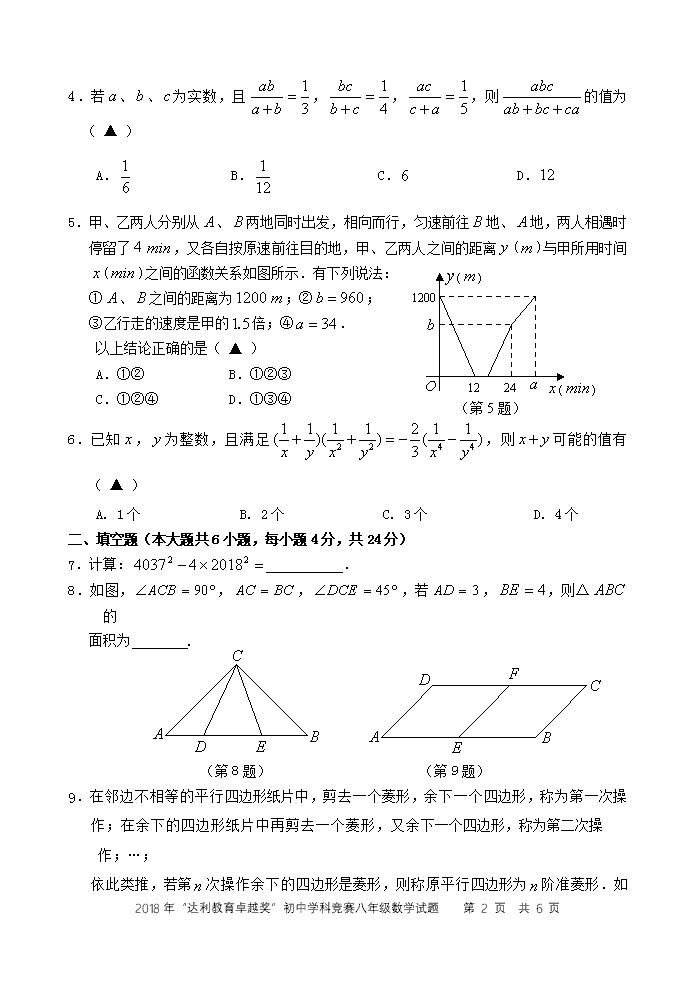
‎2018年“达利教育卓越奖”初中学科竞赛 八年级数学试题 ‎（试卷总分100分；考试时间120分钟）‎ 题号 一 二 三 总分 ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ 成绩 评卷人 一、单项选择题（本大题共6小题，每小题4分，共24分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 答案 ‎1．若，则的值是（ ▲ ）‎ ‎ A．一个奇数 B．一个质数 C．一个整数的平方 D．一个整数的立方 ‎2．如图，□中，点为边上一点，以为边作正方形，若，‎ ‎ ，则的大小为（ ▲ ）‎ ‎（第2题）‎ ‎（第3题）‎ A. B. C. D. ‎ ‎ 3．如图，在平面直角坐标系中，多边形的顶点坐标分别是(0，0)，(0，6)，(4，6)，(4，4)，(6，4)，(6，0)． 若直线经过点(2，3)，且将多边形分割成面积相等的两部分，则下列各点在直线上的是（ ▲ ）‎ ‎ A．（4，2） B．（5，3） C．（6，） D．（0，） ‎ ‎2018年“达利教育卓越奖”初中学科竞赛八年级数学试题 第 7 页 共 6 页 ‎4．若、、为实数，且，，，则的值为（ ▲ ）‎ ‎ A． B． C． D． ‎ ‎1200‎ ‎12 24‎ ‎()‎ ‎()‎ ‎（第5题）‎ ‎5．甲、乙两人分别从、两地同时出发，相向而行，匀速前往地、地，两人相遇时停留了，又各自按原速前往目的地，甲、乙两人之间的距离()与甲所用时间()之间的函数关系如图所示．有下列说法：‎ ‎①、之间的距离为；②；‎ ‎③乙行走的速度是甲的倍；④．‎ 以上结论正确的是（ ▲ ）‎ A．①② B．①②③ ‎ C．①②④ D．①③④‎ ‎6．已知，为整数，且满足，则可能的值有（ ▲ ）‎ A. 1个 B. 2个 C. 3个 D. 4个‎（第5题图）‎ 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎7．计算： ． ‎ ‎8．如图，，，，若，，则△的 ‎（第8题）‎ ‎ （第9题）‎ 面积为 . ‎ ‎9．在邻边不相等的平行四边形纸片中，剪去一个菱形，余下一个四边形，称为第一次操 作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；…；‎ 依此类推，若第次操作余下的四边形是菱形，则称原平行四边形为阶准菱形．如 ‎2018年“达利教育卓越奖”初中学科竞赛八年级数学试题 第 7 页 共 6 页 图，在□中，若，，则□为阶准菱形．若□‎ 是邻边长分别为，(＞1)，且是阶准菱形，则：‎ 的所有可能值为　 ．‎ ‎10．某客厅能被块相同的正方形地砖所铺满.若改用较小的相同正方形地砖，则需()块这样的地砖才能铺满.若与地砖的边长都是整数，则是 ．‎ ‎11．在平面直角坐标系中，(0，2)，(，)，则的最小值是 . ‎ ‎12．使得不等式对唯一的整数成立的最大正整数为 ．‎ 三、解答题（本大题共5小题，共52分）‎ ‎13．（10分）如图，凸四边形中，∥，且．‎ 求证：四边形是平行四边形．‎ ‎14．（10分）若整数，满足不等式＜，求整数，的值. ‎ ‎2018年“达利教育卓越奖”初中学科竞赛八年级数学试题 第 7 页 共 6 页 ‎15．（10分）如图，在矩形中，点在边上，，，，‎ 点，分别是边，上的点，另有一个点，使得四边形恰好为菱形，连结．设. △的面积为，试求与的函数关系式，并求出的最小值.‎ ‎2018年“达利教育卓越奖”初中学科竞赛八年级数学试题 第 7 页 共 6 页 ‎16．（10分）如图，在平面直角坐标系中，点(，)，(，)(＞)，(，)‎ ‎(＜)，点，在直线上．四边形的对角线，相交于点，且∥，，，△的面积是．‎ 求证：四边形是矩形．‎ ‎2018年“达利教育卓越奖”初中学科竞赛八年级数学试题 第 7 页 共 6 页 ‎17．（12分）如图，反比例函数的图象与一次函数的图象交于点，，点 ‎ 的横坐标是．点是第一象限内反比例函数图象上的动点，且在直线的上方．‎ ‎（1）设直线、与轴分别交于点，，求证：△是等腰三角形；‎ ‎（2）设点是反比例函数图象上位于，之间的动点(与点、不重合)，连接、，比较与的大小，并说明理由．‎ ‎2018年“达利教育卓越奖”初中学科竞赛八年级数学试题 第 7 页 共 6 页 ‎2018年“达利教育卓越奖”初中学科竞赛八年级数学试题 第 7 页 共 6 页