【数学】2021届一轮复习人教A版外接球与内切球的定心方法学案

【数学】2021届一轮复习人教A版外接球与内切球的定心方法学案

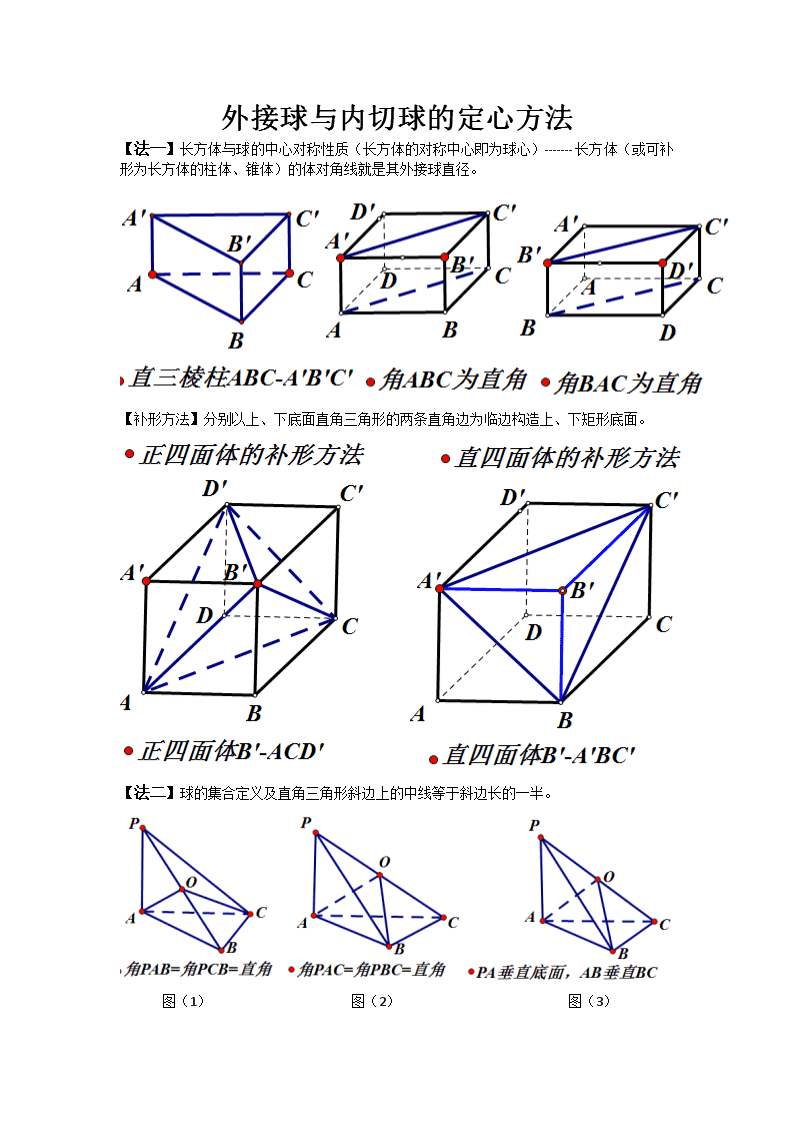
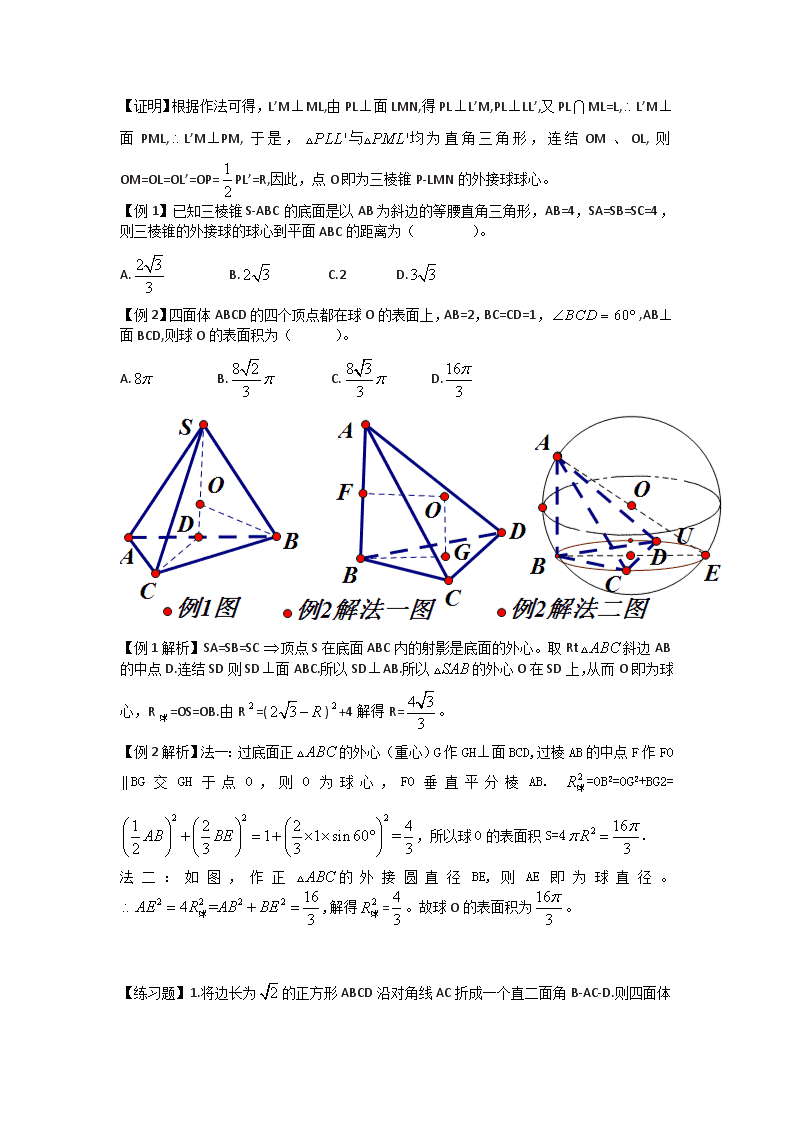
外接球与内切球的定心方法 ‎【法一】长方体与球的中心对称性质（长方体的对称中心即为球心）-------长方体（或可补形为长方体的柱体、锥体）的体对角线就是其外接球直径。‎ ‎【补形方法】分别以上、下底面直角三角形的两条直角边为临边构造上、下矩形底面。‎ ‎【法二】球的集合定义及直角三角形斜边上的中线等于斜边长的一半。‎ 图（1） 图（2） 图（3）‎ 于图（1），OA=OB=OC=OP对=PB; 对于图（2），OA=OB=OC=OP=PC; 对于图（3）, OA=OB=OC=OP=PC.‎ 根据球的集合定义可知，O为三棱锥P-ABC的外接球球心。‎ ‎【法三】射影长定理（射影线段等长斜线段等长）-------分别过几何体的两个相交平面多边形的外接圆圆心作各自平面的垂线，二垂线的交点即为外接球的球心，特别地，当一个平面（多边形）的外心恰好在另一个（下指第二个）与其相交的平面（多边形）的垂线（垂线过第二个平面多边形的外心）上时，则该外心即为几何体的外接球球心。‎ ‎【法四】过几何体的某个面的外接圆圆心作该平面的垂线与和该平面相交的某条棱的中垂线的交点即为几何体的外接球球心。‎ ‎［注］法四是法三的升级版，应用法四须使二垂线共面（否则，二垂线异面，没有交点）。‎ ‎【法 五】构造以底面外接圆直径为一条直角边，底面的垂线为另一条直角边的直角三角形，则其斜边即为该几何体的外接球直径。‎ ‎［注］法五是法二的升级版，应用了直径所对的圆周角是直角定理。‎ ‎【证明】根据作法可得，L’MML,由PL面LMN,得PLL’M,PLLL’,又PLML=L,L’M面PML,L’MPM,于是，均为直角三角形，连结OM、OL,则OM=OL=OL’=OP=PL’=R,因此，点O即为三棱锥P-LMN的外接球球心。‎ ‎【例1】已知三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形，AB=4，SA=SB=SC=4，则三棱锥的外接球的球心到平面ABC的距离为（ ）。‎ A. B. C.2 D.‎ ‎【例2】四面体ABCD的四个顶点都在球O的表面上，AB=2，BC=CD=1，,AB面BCD,则球O的表面积为（ ）。‎ A. B. C. D.‎ ‎【例1解析】SA=SB=SC顶点S在底面ABC内的射影是底面的外心。取Rt斜边AB的中点D.连结SD则SD面ABC.所以SDAB.所以的外心O在SD上，从而O即为球心，R=OS=OB.由R=()+4解得R=。‎ ‎【例2解析】法一：过底面正的外心（重心）G作GH面BCD,过棱AB的中点F作FOBG交GH于点O，则O为球心，FO垂直平分棱AB. =OB2=OG2+BG2=，所以球O的表面积S=4.‎ 法二：如图，作正的外接圆直径BE,则AE即为球直径。,解得=。故球O的表面积为。‎ ‎【练习题】1.将边长为 的正方形ABCD沿对角线AC折成一个直二面角B-AC-D.则四面体ABCD的内切球的半径为（ D ）。‎ A.1 B. C. D.‎ ‎2.已知三棱锥A-BCD的所有顶点都在球O的球面上，AB为球O的直径，若该三棱锥的体积为，BC=4，BD=,则球O的表面积为（ ）。‎ A. B. C. D. ‎ ‎3.已知A、B、C是球O的球面上三点，AB=2，AC= , 且棱锥O-ABC的体积为，则球O的表面积为（ D ）。‎ A. B. C. D.‎ ‎4.将正方形ABCD沿对角线AC折起，得到三棱锥D’-ABC的外接球的半径为，则三棱锥D’-ABC的体积为（ B ）。‎ A. B. C. D.‎ ‎5.已知点A、B、C、D在同一个球的球面上，AB=BC=,AC=2，若四面体ABCD的体积为，球心O恰好在棱DA上，则这个球的表面积为（ D ）。‎ A. B. C. D.‎ ‎6.已知一个三棱柱，其底面是正三角形，且侧棱与底面垂直，一个体积为的球体与棱柱的所有面均相切，那么这个三棱柱的表面积是（ C ）。‎ A. B. C. D.‎ ‎7.在三棱锥P-ABC中，底面ABC是等边三角形，侧面PAB是直角三角形，且PA=PB=2，当三棱锥P-ABC表面积最大时，该三棱锥外接球的表面积为（ A ）。‎ A. B. C. D.‎ ‎8.已知边长为的菱形ABCD中，,现沿对角线BD折起，使得二面角A-BD-C为,此时点A、B、C、D在同一个球面上，则该球的表面积为（C ）。‎ A. B. C. D.‎ ‎9.已知底面为正方形的四棱锥O-ABCD,各侧棱长均为，底面面积为16，以O为球心，2为半径作一个球，则这个球与四棱锥O-ABCD相交部分的体积为（ C ）。‎ A. B. C. D.‎ ‎10.设A、B、C是半径为2的球的球面上的三个不同的点，且OABC,BC=3，,则三棱锥O-ABC的体积为（ A ）。‎ A. B. C. D.‎ ‎11.如图，直三棱柱ABC-A’B’C’的六个顶点都在半径为1的半球面上，AB=AC,侧面BCC’B’是半球底面圆的内接正方形，则侧面ABB’A’的面积为（ C ）。‎ A.2 B.1 C. D.‎ ‎12.已知球的直径SC=4，A,B是该球球面是的两点，AB=2，,则棱锥S-ABC的体积为（ C ）。‎ A. B. C. D.‎ ‎13.已知圆柱的高为2，底面半径为，若该圆柱的两个底面的圆周都在同一个球面上，则这个球的表面积等于（ D ）。‎ A. B. C. D.‎ ‎14.如图，在等腰梯形ABCD中，AB=2DC=2，,E为AB的中点，将分别沿ED、EC折起，使得A,B重合于点P,则三棱锥P-DCE的外接球的体积为（ B ）。‎ A. B. C. D.‎ ‎15.已知三棱锥P-ABC的四个顶点均在某球面上，PC为该球的直径，是边长为4的等边三角形，三棱锥P-ABC的体积为，则该三棱锥的外接球的表面积为（ D ）。‎ A. B. C. D.‎