高中数学选修2-3课件2_3_1离散型随机变量的均值

高中数学选修2-3课件2_3_1离散型随机变量的均值

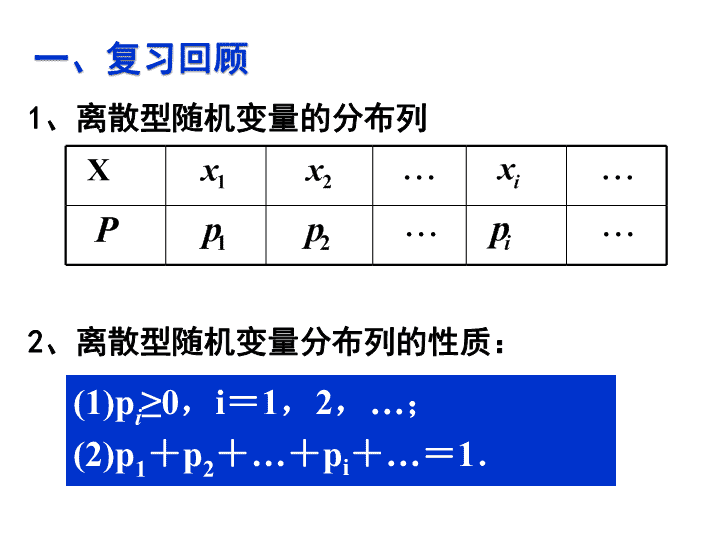
2.3.1 离散型随机变量的均值 高二数学 选修 2-3 一、复习回顾 1 、离散型随机变量的分布列 X ··· ··· ··· ··· 2 、离散型随机变量分布列的性质： (1)p i ≥0 ， i ＝ 1 ， 2 ， … ； (2)p 1 ＋ p 2 ＋ … ＋ p i ＋ … ＝ 1 ． 复习引入 对于离散型随机变量，可以由它的概率分布列确定与该随机变量相关事件的概率。但在实际问题中，有时我们更感兴趣的是随机变量的某些数字特征。例如，要了解某班同学在一次数学测验中的总体水平，很重要的是看平均分；要了解某班同学数学成绩是否“两极分化”则需要考察这个班数学成绩的方差。 我们还常常希望 直接通过数字 来反映随机变量的某个方面的特征，最常用的有 期望与方差 . 1 、某人射击 10 次，所得环数分别是： 1 ， 1 ， 1 ， 1 ， 2 ， 2 ， 2 ， 3 ， 3 ， 4 ；则所得的平均环数是多少？ 把环数看成随机变量的概率分布列： X 1 2 3 4 P 权数 加权平均 二、互动探索 2 、某商场要将单价分别为 18 元 /kg ， 24 元 /kg ， 36 元 /kg 的 3 种糖果按 3 ： 2 ： 1 的比例混合销售，如何对混合糖果定价才合理？ X 18 24 36 P 把 3 种糖果的价格看成随机变量的概率分布列： 一、离散型随机变量取值的平均值 数学期望 一般地，若离散型随机变量 X 的概率分布为： 则称 为随机变量 X 的均值或数学期望。 它反映了离散型随机变量取值的平均水平。 ··· ··· ··· ··· 设 Y ＝ aX ＋ b ，其中 a ， b 为常数，则 Y 也是随机变量． （ 1 ） Y 的分布列是什么？ （ 2 ） EY= ？ 思考： ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· 一、离散型随机变量取值的平均值 数学期望 ··· ··· ··· ··· 二、数学期望的性质 三、基础训练 1 、随机变量 ξ 的分布列是 ξ 1 3 5 P 0.5 0.3 0.2 (1) 则 Eξ= . 2 、随机变量 ξ 的分布列是 2.4 (2) 若 η=2ξ+1 ，则 Eη= . 5.8 ξ 4 7 9 10 P 0.3 a b 0.2 Eξ=7.5, 则 a= b = . 0.4 0.1 例 1. 篮球运动员在比赛中每次罚球命中得 1 分，罚不中得 0 分．已知某运动员罚球命中的概率为 0.7 ，则他罚球 1 次的得分 X 的均值是多少？ 一般地，如果随机变量 X 服从两点分布， X 1 0 P p 1 － p 则 四、例题讲解 小结： 例 2. 篮球运动员在比赛中每次罚球命中得 1 分，罚不中得 0 分．已知某运动员罚球命中的概率为 0.7 ，他连续罚球 3 次； （ 1 ）求他得到的分数 X 的分布列； （ 2 ）求 X 的期望。 X 0 1 2 3 P 解 ： (1) X ～ B （ 3 ， 0.7 ） (2) 一般地，如果随机变量 X 服从二项分布，即 X ～ B （ n,p ），则 小结： 基础训练 ： 一个袋子里装有大小相同的 3 个红球和 2 个黄球，从中有放回地取 5 次，则取到红球次数的数学期望是 . 3 1. 一次英语单元测验由 20 个选择题构成，每个选择题有 4 个选项，其中有且只有一个选项是正确答案，每题选择正确答案得 5 分，不作出选择或选错不得分，满分 100 分，学生甲选对任一题的概率为 0.9 ，学生乙则在测验中对每题都从 4 个选项中随机地选择一个。求学生甲和乙在这次英语单元测验中的 成绩 的期望。 五、巩固应用 2. 决策问题： 根据气象预报，某地区近期有小洪水的概率为 0.25 ，有大洪水的概率为 0.01 ，该地区某工地上有一台大型设备，遇到大洪水时要损失 60000 元，遇到小洪水时要损失 10000 元。为保护设备，有以下种方案： 方案 1 ：运走设备，搬运费为 3800 元。 方案 2 ：建保护围墙，建设费为 2000 元，但围墙只能 挡住小洪水。 方案 3 ：不采取措施，希望不发生洪水。 试比较哪一种方案好。 3. 某商场的促销决策： 统计资料表明，每年国庆节商场内促销活动可获利 2 万元；商场外促销活动如不遇下雨可获利 10 万元；如遇下雨则损失 4 万元。 9 月 30 日气象预报国庆节下雨的概率为 40% ，商场应选择哪种促销方式？ 4. （ 07 全国）某商场经销某商品，根据以往资料统计，顾客采用的分起付款期数 的分布列为： 1 2 3 4 5 P 0.4 0.2 0.2 0.1 0.1 商场经销一件该商品，采用 1 期付款，其利润为 200 元，分 2 期或 3 期付款，其利润为 250 元，分 4 期或 5 期付款，其利润为 300 元， 表示经销一件该商品的利润。 （ 1 ）求事件 A ：”购买该商品的 3 位顾客中，至少有一位采用 1 期付款” 的概率 P(A) ； （ 2 ）求 的分布列及期望 E 。 0.03 0.97 P 1000 － a 1000 E = 1000 － 0.03a≥0.07a 得 a≤10000 故最大定为 10000 元。 练习： 1 、若保险公司的赔偿金为 a （ a ＞ 1000 ）元，为使保险公司收益的期望值不低于 a 的百分之七，则保险公司应将最大赔偿金定为多少元？ 2 、射手用手枪进行射击，击中目标就停止，否则继续射击，他射中目标的概率是 0.7, 若枪内只有 5 颗子弹 , 求射击次数的期望。 ( 保留三个有效数字 ) 0.3 4 0.3 3 ×0.7 0.3 2 ×0.7 0.3× 0.7 0.7 p 5 4 3 2 1 E = 1.43 六、课堂小结 一、离散型随机变量取值的平均值 数学期望 ··· ··· ··· ··· 二、数学期望的性质 三、如果随机变量 X 服从两点分布， X 1 0 P p 1 － p 则 四、如果随机变量 X 服从二项分布，即 X ～ B （ n,p ），则 证明： 所以 若 ξ ～ B(n ， p) ，则 Eξ ＝ np ． 证明：若 ξ ～ B(n ， p) ，则 Eξ ＝ np