- 2021-04-14 发布 |
- 37.5 KB |
- 55页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020初中(初一)新生入学分班摸底数学考试测试卷及答案 共六套
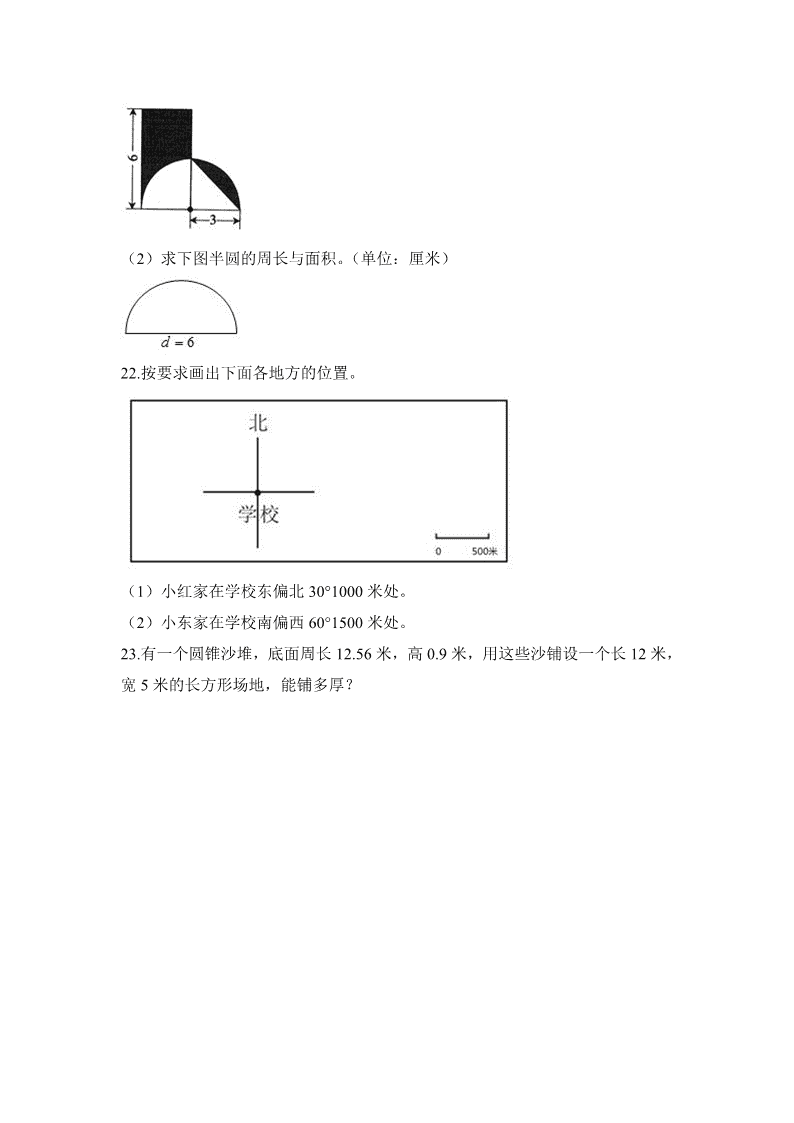
2020 初中(初一)新生入学分班摸底数学考试测试卷及答案(一) 一、填空题(共 7 题;共 7 分) 1.把 3 米长铁丝平均分成 4 段,每段是全长的________,每段________米。 2.一个仓库长60米,宽25米,高6 米,仓库占地面积________,仓库容积________。 3.把一根长 8 米的丝带剪成 10 根同样长的小段编中国结,每小段长________米, 每小段占这根丝带的 () () ________。 4.根据比值一定进行填空。 比的前项 40cm² 30cm² 比的后项 ________cm² 45cm² 5.甲数的 � � 等于乙数的 � � (甲、乙都不为 0)。甲乙两数的比是________: ________。 6.在一张标有比例尺是 8:1 的精密零件图纸上,量得零件长是 40 毫米,这个零 件实际长________。 7. � � 的倒数是 ________,2 的倒数是________。 二、判断题。(共 3 题;共 6 分) 8.假分数的倒数都小于 1. ( ) 9.圆柱体体积一定大于圆锥体体积。( ) 10.小圆半径 2 厘米,大圆半径 5 厘米,大圆面积与小圆面积之比是 5:2。( ) 三、选择题(10 分)(共 5 题;共 10 分) 11.一个比的前项扩大 10 倍,后项缩小 10 倍,则比值( )。 A. 扩大 10 倍 B. 扩大 100 倍 C. 缩小 100 倍 D. 不变 12.长方形的对称轴有________条,圆形对称轴有________条。 A、1 B、2 C、4 D、无数 13.圆的面积与它的半径( )。 A. 成正比例 B. 成反比例 C. 不成比 例 D. 没有关系 14.圆柱体的直径扩大 3 倍,高扩大 2 倍,体积扩大( )倍。 A. 6 B. 9 C. 12 D. 18 15.把一个木条钉成的长方形捏住对角,拉成一个平行四边形,它的面积比原来 的面积( )。 A. 大 B. 小 C. 相 等 D. 无法确定 四、计算题。(共 2 题;共 15 分) 16.直接写得数。 1.2×2= 0.3²= 12.4÷4= 2÷0.05= 17.脱式计算(能简算的要简算) (1)204+3.6÷3 (2)14.4÷[1-2×(1-0.95)] 五、应用题(共 6 题;共 40 分) 18. (1)画出三角形绕点 O 逆时针旋转 90°后的图形。 (2)画出三角形按 2:1 放大后的图形。 19.培智小学有学生 120 人,男生占 � � ,女生有多少人? 20.张大伯为了知道种植多少千克蔗种,采取随机抽样的方法抽取 3 千克蔗种, 剥叶砍断,按常规排列长 5 米,那么 3 亩地(沟长 2500 米)要多少千克蔗种? (用比例解) 21. (1)计算阴影部分的面积。(单位:厘米) (2)求下图半圆的周长与面积。(单位:厘米) 22.按要求画出下面各地方的位置。 (1)小红家在学校东偏北 30°1000 米处。 (2)小东家在学校南偏西 60°1500 米处。 23.有一个圆锥沙堆,底面周长 12.56 米,高 0.9 米,用这些沙铺设一个长 12 米, 宽 5 米的长方形场地,能铺多厚? 答案解析部分 一、填空题 1.【答案】 � � ; � �【考点】分数及其意义,分数与除法的关系 【解析】【解答】1÷4= � � ;3÷4= � � (米)。 故答案为: � � ; � � . 【分析】单位 1÷总段数=平均每段是全长的几分之几;铁丝长度÷平均分的段数= 每段的长度。 2.【答案】 1500 平方米;9000 立方米 【考点】长方体的体积 【解析】【解答】仓库占地面积:60×25=1500(平方米); 仓库容积:60×25×6=9000(立方米)。 故答案为:1500 平方米;9000 立方米。 【分析】仓库占地面积等于仓库的长乘以宽;仓库容积等于仓库的长宽高之积。 3.【答案】 � � ; � ��【考点】分数及其意义,分数与除法的关系 【解析】【解答】8÷10= � � (米);1÷10= � �� . 故答案为: � � ; � �� 。 【分析】丝带长度÷平均分的总段数=每段的长度;单位 1÷总段数=每段占全长的 几分之几。 4.【答案】 60 【考点】比的化简与求值 【解析】【解答】30÷45= � �40÷ � � =60 故答案为:60. 【分析】比值=比的前项÷比的后项,据此先求出比值,再进一步求出当比的前 项是 40 时后项的值。 5.【答案】 16;15 【考点】比的应用,比例的基本性质 【解析】【解答】甲数× � � =乙数× � � ; 甲数:乙数= � � : � � ; � � : � � =( � � ×20):( � � ×20)=16:15. 故答案为:16:15. 【分析】根据比例内项之积等于比例外项之积写出甲乙的比,并把比化为最简整 数比。 6.【答案】 50 毫米 【考点】应用比例尺求图上距离或实际距离 【解析】【解答】40÷8=50(毫米)。 故答案为:50 毫米。 【分析】实际距离=图上距离÷比例尺,据此解答。 7.【答案】 5; � �【考点】倒数的认识 【解析】【解答】 � � 的倒数是 5,2 的倒数是 � � . 故答案为:5; � � 。 【分析】求一个分数的倒数,就是把这个分数的分子和分母交换位置;一个整数 的倒数就是这个整数分之一。 二、判断题。 8.【答案】 错误 【考点】真分数、假分数的含义与特征 【解析】【解答】假分数的倒数都小于或等于 1,原题说法错误。 故答案为:错误。 【分析】分子比分母大或分子和分母相等的分数叫做假分数。假分数大于 1 或等 于 1,假分数的倒数都小于或等于 1。 9.【答案】 错误 【考点】圆柱与圆锥体积的关系 【解析】【解答】圆柱体体积不一定大于圆锥体体积。原题说法错误。 故答案为:错误。 【分析】圆柱体体积与圆锥体体积的大小取决于它们的底面半径和高,不知道它 们的底面半径和高,无法比较大小。 10.【答案】 错误 【考点】比的应用 【解析】【解答】 � � : � � =25:4,大圆面积与小圆面积之比是 25:4. 故答案为:错误。 【分析】圆的面积的比等于圆的半径的平方的比。 三、选择题(10 分) 11.【答案】 B 【考点】比的化简与求值 【解析】【解答】10×10=100,比值扩大 100 倍。 故答案为:B。 【分析】两个数相除,被除数扩大 m 倍,除数缩小 n 倍,商扩大 m×n 倍,据此 解答。 12.【答案】 B;D 【考点】轴对称图形的对称轴数量及位置 【解析】【解答】长方形的对称轴有 2 条,圆形对称轴有无数条。 故答案为:B;D。 【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形 就是轴对称图形,折痕所在的这条直线叫做对称轴。 13.【答案】 C 【考点】成正比例的量及其意义,成反比例的量及其意义 【解析】【解答】圆的面积与它的半径的平方成正比例,与半径不成比例。 故答案为:C。 【分析】正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这 两种量中相对应的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正 比例关系。判断正比例有一个九字口诀:相关联,能变化,商一定; 反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量 中相对应的积一定,这两种量就叫做反比例的量,它们的关系称为反比例关系。 判断反比例有一个九字口诀:相关联,能变化,积一定。 14.【答案】 D 【考点】圆柱的体积(容积),积的变化规律 【解析】【解答】3×3×2=18,体积扩大 18 倍。 故答案为:D。 【分析】圆柱体的直径扩大 3 倍,也就是半径也扩大 3 倍,则面积扩大半径的平 方倍,即 9 倍; 高扩大 2 倍,体积扩大的倍数等于底面积扩大的倍数乘以高扩大的倍数。 15.【答案】 B 【考点】平行四边形的面积,长方形的面积 【解析】【解答】长方形拉成一个平行四边形,底不变,高变小,它的面积比原 来的面积小。 故答案为:B。 【分析】长方形面积=长×宽,平行四边形面积=底×高,据此解答。 四、计算题。 16.【答案】 1.2×2=2.4 0.3²=0.09 12.4÷4=3.1 2÷0.05=40 【考点】除数是整数的小数除法,除数是小数的小数除法 【解析】【分析】小数乘法计算方法:先按整数乘法算出积,再看因数中一共有 几位小数,就从积的右边起数出几位,点上小数点; 除数是整数的小数除法:从被除数的高位除起,除数有几位,就看被除数的前几 位,如果不够除,就多看一位;除到被除数的哪一位,就把商写在哪一位的上 面,如果不够除,就在这一位上商 0;每次除得的余数必须比除数小,并在余数 右边一位落下被除数在这一位上的数,再继续除;商的小数点和被除数的小数点 对齐。 一个数除以小数,先移动除数的小数点,使它变成整数;除数的小数点向右移 动几位,被除数的小数点也向右移动几位,位数不够时,在被除数的末尾用 0 补足;最后按照除数是整数的除法进行计算。 17.【答案】 (1)204+3.6÷3 =204+1.2 =205.2 (2)14.4÷[1-2×(1- 0.95)] =14.4÷(1-2×0.05) =14.4÷(1-0.1) =14.4÷0.9 =16 【考点】小数的四则混合运算 【解析】【分析】运算顺序:先算乘除,再算加减。如果有括号,就先算括号里 面的,如果既有小括号又有中括号,由内到外,先算小括号里面的,再算中括号 里面的。 五、应用题 18.【答案】 (1) (2) 【考点】图形的缩放,将简单图形平移或旋转一定的度数 【解析】【分析】(1)旋转后图形的位置改变,转动的中心点、形状、大小不变。 因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作 图即可; (2)图形的放缩的画法:把一个图形的每条边按一定的比例放大或缩小。然后 描点、连线、绘制图形。 19.【答案】 解:120×(1- � � ) =120× � �=80(人) 答:女生有 80 人。 【考点】分数乘法与分数加减法的混合运算 【解析】【分析】学生总数×(1- � � )=女生人数,据此解答。 20.【答案】 解:设 2500 米要 x千克蔗种,则: 5:3=2500:x 5x=2500×3 5x=7500 x=7500÷5 x=1500 答:3 亩地(沟长 2500 米)要 1500 千克蔗种。 【考点】应用比例解决实际问题 【解析】【分析】根据每千克的长度相等列比例为:5 米:3 千克=2500 米:x 千 克;根据比例的基本性质把比例化为方程,根据等式性质解方程。 21.【答案】 (1)解:(6-3+6)×3÷2 =9×3÷2 =13.5(平方厘米) 答:阴影部分的面积是 13.5 平方厘米。 (2)解:3.14×6÷2+6 =9.42+6 =15.42(厘米) 3.14×(6÷2)×(6÷2)÷2 =3.14×9÷2 =28.26÷2 =14.13(平方厘米) 答:半圆的周长是 15.42 厘米,面积是 14.13 平方厘米。 【考点】圆的面积,利用平移巧算图形周长与面积 【解析】【分析】(1)平移右边的阴影部分和左边的阴影刚好拼成一个梯形,梯 形的上底是 3,下底是 6,高是 3,根据梯形面积公式求阴影部分的面积; (2)半圆的周长=圆周长的一半+直径;半圆的面积=圆的面积÷2. 22.【答案】 (1) (2) 【考点】根据方向和距离确定物体的位置 【解析】【分析】根据方向,角度,距离确定位置;根据比例尺,第一题图上距 离画 2 个线段长;第二题图上距离画 3 个线段长. 23.【答案】 解:底面半径:12.56÷3.14÷2=2(米) 沙堆体积:3.14×2×2×0.9÷3=3.14×1.2=3.768(立方米) 能铺厚度:3.768÷12÷5=0.0628(米) 答:能铺 0.0628 米。 【考点】体积的等积变形 【解析】【分析】本题属于等积变形,沙堆的体积和铺的长方形体积一样;底面 周长÷π÷2=底面半径;π×底面半径的平方×高÷3=沙堆体积;沙堆体积÷长方形的 长÷长方形的宽=长方形的高,据此解答。 2020 初中(初一)新生入学分班摸底数学考试测试卷及答案(一) 2020 初中(初一)新生入学分班摸底数学考试测试卷及答案(二) 一、填一填(每小题 2 分,共 20 分) 填上合适的单位名称: 1.)。 青青体重 40( ) 一间教室面积是 54( ) 千克。 4.2 吨=( )公顷 0.78 平方千米=( 2.)厘 3.一个圆锥的底 面半径是 3 厘米,体积为 18.84 立方厘米,这个圆锥的高是(米。 )%,也就是今 年的 今年的小麦产量比去年的增产二成三,表示今年比去年增产( 4.)%。 产 量相当于去年的( )千克。 )千克,要榨 300 千克豆油需大豆( 一种 大豆的出油率是 10%,300 千克大豆可出油( 5. )人。 一辆公共汽车共载 客 42 人,其中一部分人在中途下车,每张票价 6 元,另一部分人到终点下车, 每张票价 9 元,售票员共收票款 318 元,中途下车的有( 6. )。 ),最大 可能是( 7.一个三位小数“四舍五入”保留两位小数是 6.80,这个小数最 小可能是( )。 50 以内 6 的倍数有( 8. )分钟。 一段木头砍成 4 段要 6 分钟,砍成 8 段要( 9.)。 10.下面的图形中圆的半径为 2 ㎝,阴影 部分的面积为( 二、选择(每题 2 分,共 12 分) A.提高了 ) 一件商品,先提价 20%,以后 又降价 20%,现在的价格与原来相比,( 1. B.降低了 C.不变 D.无法确定 ) 张。 1 元和 2 角的纸币共 20 张,共 15.2 元,2 角的纸币有 ( 2. D.18 C.12 B.6 A.14 锐角、 D. 钝角 C. 直角 B. 平角 A. ) 3.在钟面上,12 时 15 分的 时候,时针和分针所成的角是( )。 4.下列图形中,对称轴最多的是( 圆 D. 等腰三角形 C. 正方形 B. 长方形 A.B.2.4 A.1.2 ) 5.两个数的比值是 1.2,如果比的前项扩大 2 倍,后 项缩小两倍,比值是( C.4.8 D.9.6)小时。 6.王师傅加工 一批零件,1/2 小时加工了这批零件的 3/8,全部加工完还需要( 三、判断(6 分) ) 长方体的底面积一定,高和体积成反比例。( 3. ) 一个圆和一个正 方形的周长相等,比较它们的面积,结果是圆的面积大。( 2. ) ( 在 一个比例里,如果内项的积等于 1,那么两个外项的积一定是 1。 1. ) 两条线段互相平行,它们也一定相等。( 5. ) 小刚在教室中的座位用数对 表示为(3,5),代表着他坐在第三行第五列。( 4.) ( 盒子里有同样大 小的红、黄、蓝三种颜色的球各 5 个,要想摸出的球一定有 2 个是同色的,至少 要摸出 4 个球。 6. 四、算一算。 (共 26 分) 分) 能简算的要简算。(12 1. 求未知数的值。(9 分) 2. 3.图中的两个正方形的边长分别是 10 厘米和 6 厘米,求阴影部分的面积. 五、应用题。(每小题 5 分,共 30 分) 一个等腰三角形,底角和顶角的度数比是 1:3。它的一个底角是多少 度? 1. 新区器材厂用一根长 120 厘米的铁丝做成一个长方体框架,这个长 方体长宽高的比是 3:2:1,这个长方体的体积是多少立方厘米? 2. 公园里栽了 149 棵杨树,再栽上 22 棵就是所栽柳树的 3 倍。栽了多少棵柳树? (用方程解答) 3.kg,茄子的质量比土豆的 3 倍还多 8kg,茄子和土豆各有多 少千克? 食堂买来茄子和土豆共 380 4. 儿童节期间,学校准备用 800 元钱买节日礼物,其中 30%的钱买糖果,剩余的钱按 3:5 用来购买文具和图书。 学校购买文具和图书各用了多少元? 5.一个圆柱形的游泳池,底面直径是 10 米, 高是 4 米。在它的四周和底部涂水泥,每千克水泥可涂 5 平方米,共需多少千克 水泥? 6. 六、图图变换(6 分) 画出三角形 AOB 绕点 0 点逆时针旋转 90°后的图形。 参考答案: 2020 初中(初一)新生入学分班摸底数学考试测试卷及答案(三) 一、直接写出下列各题的得数。(共 6 分) 二、填空。(16 分) 1、由 1、2、3 这三个数字能组成的三位数一共有( )个,它们的和是( )。 2、一道除式,商是 22,余数是 6,被除数与除数的和是 259,这道除式的除数是( ),被 除数是( )。 3、甲乙两数的最小公倍数是 78,最大公约数是 13,已知甲数是 26,乙数是( )。 4、小明有 15 本故事书,比小英的 3 倍多 a 本,小英有( )本故事书。 5、两个数相除的商是 7.83,如果把被除数和除数的小数点同时向右移动一位,商是( )。 6、一个比例的两个内项互为倒数,它的一个外项是 0.8,另一个外项是( )。 7、单独完成同一件工作,甲要 4 天,乙要 5 天,甲的工作效率是乙的( )%。 8、一个带小数的整数部分与小数部分的值相差 88.11,整数部分的值恰好是小数部分的 100 倍,这个数是( )。 三、选择正确答案的序号填在题中的括号里。(20 分) 1、圆有( )对称轴. A.1 条 B.2 条 C.4 条 D.无数条 2、5 米增加它 的之后,再减少 米,结果是( ) A. B. C.5 米 D.7 米 3、气象台表示一天中气温变化的情况,采用( )最合适。 A.统计表 B.条形统计图 C.扇形统计图 D.折线统计图 4、五年级同学参加科技小组的有 23 人,比参加书法小组人数的 2 倍多 5 人,如果设书法 小组有 x 人,则正确的方程是( ) A.2( x+5)=23 B.2x+5=23 C.2x=23-5 D.2x-5=23 5、一根钢管,截去部分是剩下部分的 1/4,剩下部分是原钢管长的( )%。 A.75 B.400 C.80 D.25 6、等底等体积的圆柱和圆锥,圆锥高是 9 米,圆柱高是( ) A.9 米 B.18 米 C.6 米 D.3 米 7、一个长方体的长、宽、高分别是 a 米、b 米和 h 米,如果高增加 3 米,体积增加( ) 立方米。 A.3ab B.3abh C.ab(h+3) D.3bh 8、把 24 分解质因数是( ) A.24=3×8 B.24=2×3×4 C.24=2×2×2×3 D.24=6×4×1 9、乙数比甲数少 40%,甲数和乙数的比是( ) A.2:3 B.3:2 C.3:5 D.5,3 10、甲把自己的钱的 1/3 给乙以后,甲、乙两人钱数相等,甲、乙原有钱数的比是( ) A.2:3 B.3:2 C.3:5 D.5:3 四、用递等式计算(12 分) 1042-384÷16×13 4.1-2.56÷(0.18+0.62) 3.14×43+7.2×31.4-150×0.314 五、解答题。(9 分) 1、下图中,长方形被两条直线分成四个小长方形,其中三个的面积分别是 12 平方米、8 平方米、20 平方米,求另一个(图中阴影都分)长方形的面积。(5 分) 2、求阴影部分的面积(单位:米)。(4 分) 六、列式解答。(12 分) 1、甲数的 25%是 1.25,乙数是 60 的 20%,乙数是甲数的百分之几。 2、4 加上一个数的 75%等于 11.5,求这个数。 3、8 减去 4/9 除以 1/3 的商,所得的差乘 4/5,积是多少? 七、应用题。(共 25 分) 1、一条长 1500 米的水渠横截面如下图所示,求挖成这条水渠需要挖土多少立方米? 2、某车队运一堆煤,第一天运走这堆煤的 1/6,第二天比第一天多运 30 吨,这时已运走的 煤与余下煤吨数比是 7:5,这堆煤共有多少吨? 3、一列慢车和一列快车分别从 A、B 两站相对开出,快车和慢车速度的比是 5:4,慢车先从 A 站开出 27 千米,快车才从 B 站开出。相遇时快车和 B 站的距离比慢车和 A 站的距离多 32 千米,A、B 两站相距多少千米? 4、有两个粮仓,已知甲仓装粮 600 吨,如果从甲仓调出粮食 1/3,从乙仓调出粮食 75%后, 这时甲仓的粮食比乙仓的 2 倍还多 150 吨,乙仓原有粮食多少吨? 5、一个圆柱体,底面半径是 7 米,表面积是 1406.72 平方厘米。这个圆柱的高是多少? 参考答案 一、 7/12 1/8 1 10 0.4 0.75 1 2/3 13/30 901 15.3 5 二、 1、6 1332 2、11 248 3、39 4、(15-a)/3 5、7.83 6、1.25 7、125 8、89.89 三、 1、D 2、D 3、D 4、B、C 5、C 6、D 7、A 8、C 9、C 10、C 四、 730 0.9 314 五、略 六、略 七、略 2020 初中(初一)新生入学分班摸底数学考试测试卷及答案(四)1.(1 分)0.47÷0.4,商是 1.1,余数是( ) A.3 B.0.3 C.0.03 2.(1 分)一个小数四舍五入得 8.60,原来这个小数最小是( ) A.8.601 B.8.605 C.8.595 3.(1 分)能被 3、5 整除的最小三位数是( ) A.100 B.105 C.120 4.(1 分)已知甲数=2×2×3×5,乙数=2×3×5×7,那么甲数和乙数的最大公约数是 ,最 小公倍数是 A.12 B.420 C.30 D.60 5.(4 分)在横线里填上<、>或=. 9.78×0.8 9.78; 9.56÷1.02 9.56; 4.05×1.15 4.05×0.99; 8.6÷0.2 8.6×5. 6.(5 分)填写发票. 住户 2 月份电费: 住户 上月读数 本月读数 实用数(千瓦时) 单价(元) 金额(元) 101 1572 1641 0.53 202 801 859 0.53 合计 人民币(大写): 7.(6 分) 正确互化. 3 分米= 米 25 平方厘米= 平方分米 12 分= 小时 50 立方分米= 立方米 40 小时= 日 650 克= 千克 8.(13 分)分别用 5 个、7 个、9 个、13 个和 18 个小正方形拼长方形(含正方形),各能拼几个?你有 什么发现? 小正方形的个数 拼出的长方形个数 长、宽各是几 你的发现 5 7 9 13 18 9.(1 分)用 1、2、3、4、0 这些数字可以组成( )能同时被 2、3、5 整除的四位数. A.6 个 B.12 个 C.3 个 D.无数个 10.(16 分)直接写出得数 4.38 6.62= 10﹣0.01= 7.4﹣2.93﹣ 3.07= 1.25×3.2= 6.4÷0.25= 1﹣﹣﹣= 6.5÷12.5= 2 = 0.85= 0.25= 1.4 = 1 0.4 2= 1= 4.1﹣2= 5﹣3.49 1= 25﹣(3 2)= 11.(6 分)解方程 7x 2.5=8.8; 4×(x﹣2.8)=26.4; 7.2÷(x 0.38)=8. 12.(15 分)递等计算. 18.8÷0.1﹣150; 19﹣(10﹣4); 7.2﹣(3﹣10÷3 1); 14﹣2.75 1.25﹣3; [(30﹣19.8)×0.25﹣2.05]÷2.5. 13.(3 分)9.6 的一半加 4 除 1 的商,和是几? 14.(3 分)4.5 加一个数减 3 的差,结果是 9.这个数是多少? 15.(4 分)求图中阴影部分的面积.(单位:米) 16.(4 分)一条刚修建好的公路需要绿化,已经完成了 45.3 千米,剩下的比已经完成的 3 倍多 10.8 千 米.这条公路全长多少千米? 17.(4 分)虾每千克 21.5 元,鱼每千克 11.4 元,妈妈买了 0.6 千克虾和 1 千克鱼,付出 30 元,应找回 多少元? 18.(4 分)一根长方体木料,长 2.8 米,横截面是正方形,将它锯成 3 段以后,表面积增加了 144 平方 厘米.原来这根木料的表面积是多少? 19.(4 分)生产 300 个零件,王师傅单独做需要 10 小时完成,张师傅单独做需要 12 小时完成.现在两 人合作 3 小时,还剩下多少个? 20.(4 分)小车一次能运 2 吨,比大车一次少运 3.4 吨.一批货物有 10 吨,大车和小车各运一次后还剩 下多少吨? 21.(10 分)跳一跳,摘“桃子”. 一个用搭成的实心模型,从前面、上面和右面观察,看到的分别是下面三个图.这个实心模型共有几个? 参考答案 1.C 【解析】 试题分析:根据有余数的除法可知,商×除数 余数=被除数,那么余数=被除数﹣商×除数,代入数据进行 解答即可. 解:根据题意可得: 余数是:0.47﹣1.1×0.4=0.47﹣0.44=0.03. 故选:C. 点评:被除数=商×除数 余数,同样适用于小数的除法. 2.C 【解析】 试题分析:要考虑 8.60 是一个两位数的近似数,有两种情况:“四舍”得到的 8.60 最大是 8.604,“五 入”得到的 8.60 最小是 8.595,由此解答问题即可. 解:一个小数四舍五入得 8.60,原来这个小数最小是 8.595; 故选:C. 点评:取一个数的近似数,有两种情况:“四舍”得到的近似数比原数小,“五入”得到的近似数比原数 大,根据题的要求灵活掌握解答方法. 3.B 【解析】 试题分析:能同时被 3、5 整除的数必须具备:个位上的数是 0 或 5,各个数位上的数的和能够被 3 整除; 据此解答. 解:A,100 的数字和是 1,不能被 3 整除; B、105 的数字和 1 5=6,6÷3=2 能被 5 整除,个位数字是 5,能被 5 整除; 105<120 答:能被 3、5 整除的最小三位数是 105. 故选:B. 点评:此题考查能被 2、3、5 整除的数的特征,要注意是求能同时被 2、3、5 整除的最小三位数. 4.C,B 【解析】 试题分析:求最大公约数也就是这几个数的公有质因数的连乘积,最小公倍数是公有质因数与独有质因数 的连乘积,对于两个数来说:两个数的公有质因数连乘积是最大公约数,两个数的公有质因数与每个数独 有质因数的连乘积是最小公倍数,由此解决问题即可. 解:甲数=2×2×3×5,乙数=2×3×5×7,那么, 甲、乙两数最大公约数为:2×3×5=30 最小公倍数是:2×2×3×5×7=420 故选:C,B. 点评:此题主要考查求两个数的最大公约数与最小公倍数的方法:两个数的公有质因数连乘积是最大公约 数,两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数. 5.<,<,>,=. 【解析】 试题分析:一个数(0 除外)乘一个小于 1 的数和除以大于 1 的数,得到的结果小于它本身;一个数(0 除 外)除以一个小于 1 的数和乘大于 1 的数,得到的结果大于它本身.依此比较即可. 解:9.78×0.8<9.78; 9.56÷1.02<9.56; 4.05×1.15>4.05×0.99; 8.6÷0.2=8.6×5 故答案为:<,<,>,=. 点评:不用计算,根据一个数乘或者除以的数比 1 大还是比 1 小进行比较. 6. 住户 2 月份电费: 住户 上月读数 本月读数 实用数(千瓦时) 单价(元) 金额(元) 101 1572 1641 69 0.53 36.57 202 801 859 58 0.53 30.74 合计 人民币(大写): 陆 拾 柒 元 叁 角 壹 分 【解析】 试题分析:用本月读数减去上月读数,可求出实用数,再根据总价=单价×数量,可求出各个住户的钱数, 把各户的金额相加,就是合计.据此解答. 解:1641﹣1572=69(千瓦时) 69×0.53=36.57(元) 859﹣801=58(千瓦时) 58×0.53=30.74(元) 36.57 30.74=67.31(元) 住户 2 月份电费: 住户 上月读数 本月读数 实用数(千瓦时) 单价(元) 金额(元) 101 1572 1641 69 0.53 36.57 202 801 859 58 0.53 30.74 合计 人民币(大写): 陆 拾 柒 元 叁 角 壹 分 点评:本题主要考查了学生观察统计表分析数量关系解答问题的能力. 7.0.3,0.25,0.2,0.05,1,0.65. 【解析】 试题分析:把 3 分米换算成米数,用 3 除以进率 10; 把 25 平方厘米换算成平方分米数,用 25 除以进率 100; 把 12 分换算成小时数,用 12 除以进率 60; 把 50 立方分米换算成立方米数,用 50 除以进率 1000; 把 40 小时换算成日数,用 40 除以进率 24; 把 650 克换算为千克,用 650 除以进率 1000. 解: 3 分米=0.3 米 25 平方厘米=0.25 平方分米 12 分=0.2 小时 50 立方分米=0.05 立方米 40 小时=1 日 650 克=0.65 千克 故答案为:0.3,0.25,0.2,0.05,1,0.65. 点评:此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位 的名数换算成高级单位的名数,就除以单位间的进率. 8. 小正方形的个 数 拼出的长方形个 数 长、宽各是几 你的发现 5 1 5、1 质数都只能排出一种,其他的找约数,长、宽就是这些 约数. 7 1 7、1 9 2 9、1 或 3、3 13 1 13、1 18 3 1、18;2、9 或 3、 6 【解析】 试题分析:因为 5=1×5,7=1×7,9=3×3=1×9,13=1×13,18=2×9=3×6=1×18,所以分别用 5 个、7 个、 9 个、13 个和 18 个小正方形拼长方形(含正方形)得个数分别为 1 个、1 个、2 个、1 个、3 个,从而发现: 质数都只能排出一种,其他的找约数,长、宽就是这些约数;据此解答. 解:由分析可得: 小正方形的个 数 拼出的长方形个 数 长、宽各是几 你的发现 5 1 5、1 质数都只能排出一种,其他的找约数,长、宽就是这些 约数. 7 1 7、1 9 2 9、1 或 3、3 13 1 13、1 18 3 1、18;2、9 或 3、 6 点评:此题考查了正方形拼组长方形问题,注意这里所说的长方形包含正方形. 9.B 【解析】 试题分析:能同时被 2、3、5 整除的数必须具备:个位上的数是 0,各个数位上的数的和能够被 3 整除; 据此解答. 解:用 1、2、3、4、0 这些数字可以组成能同时被 2、3、5 整除的四位数首先选数字 0(放在个位,满足 能被 2、和 5 整除),然后选 1、2、3 或 2、3、4(和能被 3 整除),组成的数字有:1230、1320、2130、 2310、3120、3210;2340、2430、3240、3420、4230、4320 共 12 个数字; 故选:B. 点评:此题考查能被 2、3、5 整除的数的特征,要注意是求能同时被 2、3、5 整除的四位数. 10.11;9.99;1.4;4;25.6;0;0.52;3;1.75;;2;4.2;1.75;2.05;3.51;19; 【解析】 试题分析:(1)(2)注意小数点对齐;(3)运用减法的性质简算;(4)把 1.25 化成分数,约分计算; (5)把被除数和除数分别扩大 100 倍,再相除;(6)运用减法的性质简算;(7)把被除数和除数分别扩 大 10 倍,再相除;(8)通分计算;(9)(11)(12)(14)把分数化为小数计算简便;(10)把小数化 为分数计算简便;(13)先把化成小数,然后加上 1;(15)运用加法交换律与结合律简算;(16)先算 括号内的,再算括号外的. 解: 4.38 6.62=11 10﹣0.01=9.99 7.4﹣2.93﹣3.07=1.4 1.25×3.2=4 6.4÷0.25=25.6 1﹣﹣﹣=0 6.5÷12.5=0.52 2 =3 0.85=1.75 0.25= 1.4 =2 1 0.4 2=4.2 1=1.75 4.1﹣2=2.05 5﹣3.49 1=3.51 25﹣(3 2)=19 点评:此题考查了小数和分数的四则混合运算,注意数字转化以及简便计算. 11.0.9;9.4;0.52; 【解析】 试题分析:①方程的两边同时减去 2.5,然后再同时除以 7 即可得到未知数的值. ②方程的两边同时加上 11.2,然后再同时除以 4 即可得到未知数的值. ③方程的两边同时乘以(x 0.38),然后方程的两边同时减去 0.38 即可得到未知数的值. 解:①7x 2.5=8.8 7x 2.5﹣2.5=8.8﹣2.5 7x=6.3 7x÷7=6.3÷7 x=0.9 ②4×(x﹣2.8)=26.4 4x﹣11.2=26.4 4x 11.2﹣11.2=26.4 11.2 4x=37.6 4x÷4=37.6÷4 x=9.4 ③7.2÷(x 0.38)=8 7.2×(x 0.38)÷(x 0.38)=8×(x 0.38) 8×(x 0.38)÷8=7.2÷8 x 0.38=0.9 x 0.38﹣0.38=0.9﹣0.38 x=0.52 点评:本题运用等式的基本性质进行解答即可,注意等于号要对齐. 12.38;14;;;0.2. 【解析】 试题分析:(1)先算除法,再算减法. (2)运用减法的性质以及加法结合律简算. (3)先算括号内的除法,再算括号内的减法和加法,最后算括号外的减法. (4)运用加法交换律与结合律以及减法的性质简算. (5)先算小括号内的,再算中括号内的乘法,最后算括号外的除法. 解:(1)18.8÷0.1﹣150 =188﹣150 =38 (2)19﹣(10﹣4) =19﹣10 4 =9 4 =14 (3)7.2﹣(3﹣10÷3 1) =7.2﹣(3﹣3 1) =7﹣ = (4)14﹣2.75 1.25﹣3 =(14﹣3)﹣(2.75﹣1.25) =﹣1.5 =﹣ = (5)[(30﹣19.8)×0.25﹣2.05]÷2.5 =[10.2×0.25﹣2.05]÷2.5 =[2.55﹣2.05]÷2.5 =0.5÷2.5 =0.2 点评:考查了小数、分数的四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律或运算性 质进行简便计算. 13.5.05. 【解析】 试题分析:9.6 的一半是 9.6÷2,4 除 1 的商是 1÷4,然后求二者之和,由此列式解答. 解:9.6÷2 1÷4 =4.8 0.25 =5.05 答:和是 5.05. 点评:解答此题应注意“除”与“除以”的区别. 14.9 【解析】 试题分析:用方程解答.设这个数是 x,得 4.5 加这个数为 4.5 x,然后减去 3,等于 9,由此列出方程即 可. 解:设这个数是 x,得 4.5 x﹣3=9 x 0.9=9.9 x=9 答:这个数是 9. 点评:明确数量间的等量关系,并根据它们之间的关系列方程,依据等式的性质解答是本题考查知识点. 15.4.5 平方米 【解析】 试题分析:根据三角形的面积=底×高÷2,可求出阴影部分的面积. 解:3×3÷2 =9÷2 =4.5(平方米) 答:阴影部分的面积是 4.5 平方米. 点评:本题的关键是找到阴影部分三角形的底和高,再根据三角形的面积公式进行计算. 16.192 千米. 【解析】 试题分析:剩下的比已经完成的 3 倍多 10.8 千米,即:剩下的量=已完成的量×3 10.8,据此求出剩下多 少千米,再加上已经完成的 45.3 千米,即为这条公路全长多少千米. 解:45.3×3 10.8 45.3 =135.9 10.8 45.3 =192(千米) 答:这条公路全长 192 千米. 点评:解答本题的关键是得出:剩下的量=已完成的量×3 10.8. 17.5.7 元. 【解析】 试题分析:运用乘法分别求出 0.6 千克虾和 1 千克鱼的钱数,用 30 元减去鱼、虾的钱数的和,即为应找回 多少元. 解:30﹣(21.5×0.6 11.4×1) =30﹣(12.9 11.4) =30﹣24.3 =5.7(元) 答:付出 30 元,应找回 5.7 元. 点评:本题主要运用乘法的意义,求出 0.6 千克虾和 1 千克鱼的钱数. 18.6792 平方厘米. 【解析】 试题分析:将它锯成 3 段以后,表面积增加了 144 平方厘米,即增加了 4 个底面的面积,用“144÷4”求 出底面积,进而推断出底面边长,然后根据:长方体的表面积=(长×宽 长×高 宽×高)×2,解答即可. 解:2.8 米=280 厘米 144÷4=36(平方厘米), 因为 6×6=36,所以该长方体木料的底面边长是 6 厘米, 则表面积为:(6×6 6×280 6×280)×2 =3396×2 =6792(平方厘米) 答:原来这根木料的表面积是 6792 平方厘米. 点评:此题属于简单的立方体切拼问题,明确将它锯成 3 段以后,表面积增加了 144 平方厘米,即增加了 4 个底面的面积,是解答此题的关键. 19.135 个 【解析】 试题分析:把零件个数看作单位“1”,先表示出王师傅和张师傅的工作效率,再依据工作总量=工作时间 ×工作效率,求出两人 3 小时完成零件个数占这个数的分率,进而求出剩余零件个数占这个数的分率,最 后运用分数乘法意义即可解答. 解:300×[1﹣()×3] =300×[1﹣] =300× =135(个) 答:还剩下 135 个. 点评:解答本题的关键是求出剩余零件个数占这个数的分率,也就是分数乘法意义. 20.2.225 吨. 【解析】 试题分析:根据题意,先求出大车一次能运的吨数,再求出大车和小车各运一次能运的吨数,进而根据减 法的意义,用货物的总吨数减去运走的吨数,就是还剩下的吨数. 解:10﹣(2 3.4 2) =10.625﹣(2.5 3.4 2.5) =10.625﹣8.4 =2.225(吨). 答:大车和小车各运一次后还剩下 2.225 吨. 点评:此题考查分数加减法应用题,只要分清数量之间的关系,搞清要计算的顺序,问题容易解决. 21.8 个 【解析】 试题分析:从前面看,能看到 6 个,接着从上面看第一行有 4 个,第二行至少有 1 个,然后再从右面看有 两层,每层都有 2 个,所以这个实心模型第一层有 4 1=5 个,第二层有 3,然后相加即可. 解:根据观察可得: 4 1 3=8(个) 答:该模型共有 8 个小正方体组成. 点评:此模型有若干个正方体组成,根据不同位置观察到的图形,可以动手操作排一排,看一看,也是解 决问题的好办法. 2020 初中(初一)新生入学分班摸底数学考试测试卷及答案(五) 一、选择题:(每小题 4 分,共 16 分) 1、在比例尺是 1:4000000 的地图上,量得 A、B 两港距离为 9 厘米, 一艘货轮于上午 6 时以每小时 24 千米的速度从 A 开向 B 港,到达 B 港的时间是( )。 A、15 点 B、17 点 C、19 点 D、21 点 2、将一根木棒锯成 4 段需要 6 分钟,则将这根木棒锯成 7 段需要( ) 分钟。 A、10 B、12 C、14 D、16 3、一个车间改革后,人员减少了 20%,产量比原来增加了 20%,则工 作效率( )。 A、提高了 50% B、提高 40% C、提高了 30% D、与 原来一样 4、A、B、C、D 四人一起完成一件工作,D 做了一天就因病请假了,A 结果做了 6 天,B 做了 5 天,C 做了 4 天,D 作为休息的代价,拿出 48 元给 A、B、C 三人作为报酬,若按天数计算劳务费,则这 48 元中 A 就分( )元。 A、18 B、19.2 C、20 D、32 二、填空题:(每小题 4 分,共 32 分) 1、学校开展植树活动,成活了 100 棵,25 棵没活,则成活率是( )。 2、甲乙两桶油重量差为 9 千克,甲桶油重量的 1/5 等于乙桶油重量 的 1/2,则乙桶油重( ) 千克。 3、两个自然数的差是 5,它们的最小公倍数与最大公约数的差是 203, 则这两个数的和是( )。 4、一个圆锥与一个圆柱的底面积相等,已知圆锥与圆柱的体积比是 1:6,圆锥的高是 4.8 厘米,则圆柱的高是( )厘米。 5、如图,电车从 A 站经过 B 站到达 C 站,然后返回。去时 B 站停车, 而返回时不停,去时的车速为每小时 48 千米,返回时的车速是每小 时( )千米。 6、扑克牌游戏,小明背对小亮,让小亮按下列四个步骤操作: 第一步,分发左中右三堆牌,每堆牌不少于两张,且各堆牌的张数相 同; 第二步,从左边一堆拿出两张,放入中间一堆; 第三步,从右边一堆拿出一张,放入中间一堆; 第四步,左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆。 这时小明准确说出了中间一堆牌现有的张数,你认为中间一堆牌现有 的张数是( )。 7、 前 30 个数的和为( )。 8、如图已知直角三角形的面积是 12 平方厘米,则阴影部分的面积是 ( )。 三、计算:(每小题 5 分,共 10 分) 四、列式计算:(4 分) 10.2 减去 2.5 的差除以 20%与 2 的积,商是多少? 五、应用题:(共 38 分) 1、已知相邻两根电线杆之间的距离是 35 米,从小洪家到学校门口有 36 根电线杆,再往前 595 米,共有多少根电线杆?(6 分) 2、工程队用 3 天修完一段路,第一天修的是第二天的 9/10,第三天 修的是第二天的 6/5 倍,已知第三天比第一天多修 270 米,这段路长 多少米?(6 分) 3、运动员在公路上进行骑摩托车训练,速度为 90 千米,出发时有一 辆公共汽车和摩托车同时出发并同向行驶。公共汽车的行驶速度 60 千米,摩托车跑完 80 千米掉头返回,途中和公共汽车相遇,这次相 遇是在出发后多长时间? 4、某商店到苹果产地收购了 2 吨苹果,收购价为每千克 1.20 元,从 产地到商店的距离是 400 千米,运费为每吨货物每运 1 千米收 1.50 元,如果在运输及销售过程中的损耗为 10%,那么商店要实现的 15% 的利润率,零售价就是每千克多少元? 5、同学在 A、B 两家超市发现他看中的随身听的单价相同,书包单价 也相同,随身听和书包单价之和是 452 元,且随身听的单价比书包单 价的 4 倍少 8 元。某天该同学上街,恰好赶上商家促销,超市 A 所有 的商品打八折销售,超市 B 全场购物满 100 元返 30 元购物券(不足 100 不返券,购物券全场通用),但他只带了 400 元钱,若两家都可 以选择,在哪一家购买较省钱?为什么? 参考答案 一、D、B、A、D 二、80%、6、29、9.6、76、5、30/31、3.42、 三、1、1/2;2、6.3。 四、9 又 5/8 五、1、53 根;2、2790 米;3、64 千米;4、2.3 元;5、360 元;在 A 超市 2020 初中(初一)新生入学分班摸底数学考试测试卷及答案(六)查看更多