江苏省金陵中学丹阳高级中学无锡一中2020届高三下学期期初联考数学试题
2020届高三年级第二学期期初联考试卷
数学试题
Ⅰ试题
一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)
1.已知集合A={1,2,3},B={2,4},则A∪B= ▲ .
2.已知复数z1=-2+i,z2=a+2i(i为虚数单位,a∈R),若z1z2为纯虚数,则实数a的值为 ▲ .
3.函数f(x)=ln(x-1)的定义域为 ▲ .
4.某人5次上班途中所花的时间(单位:分钟)分别为12,x,10,11,9.已知这组数据的平均数为10,方差为2,则x的值为 ▲ .
5.已知抛物线y2=4x上一点的距离到焦点的距离为5,则这点的坐标为 ▲ .
6.已知命题p:-1
0,若p是q的充分不必要条件,则实数a的取值范围是 ▲ .
7.等比数列{an}的前n项和为Sn,若4a1,2a2,a3成等差数列,a1=1,则S7= ▲ .
8.函数f(x)是在R上的周期为3的奇函数,当0c-1的解集为(m-4,m),则实数c的值为 ▲ .
12.在锐角△ABC中,已知sinC=4cosAcosB,则tanAtanB的最大值为 ▲ .
13.在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC
的平分线交AC于点D,且BD=1,则4a+c的最小值为 ▲ .
14.设函数f(x)=ax+sinx+cosx.若函数f(x)的图象上存在不同的两点A,B,使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为 ▲ .
二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)
15.(本小题满分14分)
如图,在三棱锥A-BCD中,E,F分别为棱BC,CD上的点,且BD∥平面AEF.
(1)求证:EF∥平面ABD;
A
B
C
F
E
D
(第15题)
(2)若BD⊥CD,AE⊥平面BCD,求证:平面AEF⊥平面ACD.
16.(本小题满分14分)
在△ABC中,内角A,B,C所对的边分别为a,b,c,cosB=.
(1)若c=2a,求的值;
(2)若C-B=,求sinA的值.
17.(本小题满分14分)
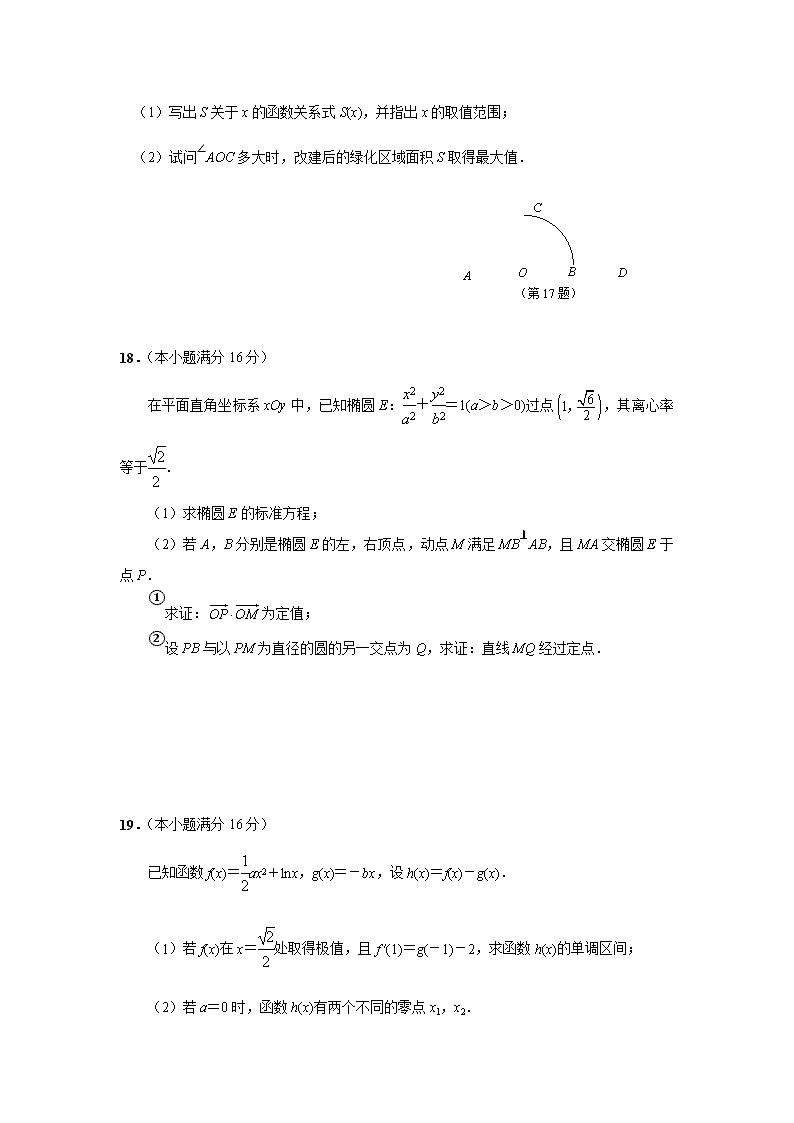
如图,某城市有一块半径为40 m的半圆形绿化区域(以O为圆心,AB为直径),现计划对其进行改建.在AB的延长线上取点D,OD=80 m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2.设∠AOC=x rad.
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)试问∠AOC多大时,改建后的绿化区域面积S取得最大值.
A
B
O
C
D
(第17题)
18.(本小题满分16分)
在平面直角坐标系xOy中,已知椭圆E:+=1(a>b>0)过点,其离心率等于.
(1)求椭圆E的标准方程;
(2)若A,B分别是椭圆E的左,右顶点,动点M满足MB⊥AB,且MA交椭圆E于点P.
①求证:为定值;
②设PB与以PM为直径的圆的另一交点为Q,求证:直线MQ经过定点.
19.(本小题满分16分)
已知函数f(x)=ax2+lnx,g(x)=-bx,设h(x)=f(x)-g(x).
(1)若f(x)在x=处取得极值,且f ′(1)=g(-1)-2,求函数h(x)的单调区间;
(2)若a=0时,函数h(x)有两个不同的零点x1,x2.
①求b的取值范围;
②求证:x1·x2>e2.
20.(本小题满分16分)
已知数列{an}前n项和为Sn,数列{an}的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,且满足S5=2a4+a5,a9=a3+a4.
(1)求数列{an}的通项公式;
(2)若amam+1=am+2,求正整数m的值;
(3)是否存在正整数m,使得恰好为数列{an}中的一项?若存在,求出所有满足条件的m值,若不存在,说明理由.
2020届高三年级第二学期期初联考试卷
数学试题
命题单位:丹阳高级中学
审核单位:金陵中学 无锡一中
Ⅱ试题
21.【选做题】在A、B、C三小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
A.选修4—2:矩阵与变换
设a,b∈R.若直线l:ax+y-7=0在矩阵A= 对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
B.选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,直线l:(t为参数),与曲线C:(k为参数)交于A,B两点,求线段AB的长.
C.选修4—5:不等式选讲
已知x,yR,且|x+y|≤,|x-y|≤,求证:|x+5y|≤1.
【必做题】第22题、第23题,每题10分,共计20分.请在答卷卡指定区域内
作答.解答应写出文字说明、证明过程或演算步骤.
22.(本小题满分10分)
某中学有4位学生申请A,B,C三所大学的自主招生.若每位学生只能申请其中一所大学,且申请其中任何一所大学是等可能的.
(1)求恰有2人申请A大学的概率;
(2)求被申请大学的个数X的概率分布列与数学期望E(X).
23.(本小题满分10分)
已知…,.记.
(1)求的值;
(2)化简的表达式,并证明:对任意的,都能被整除.
期初联考试卷 数学试题参考答案及评分标准
Ⅰ试题
一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)
1.{1,2,3,4} 2.-1 3.(1,+∞) 4.8 5.(4,±4)
6.[5,7] 7.127 8.-2 9.3:2 10.
11.-3 12.4 13.9 14.[-1,1]
二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)
15.(本小题满分14分)
解:(1)因为BD∥平面AEF,BDÌ平面BCD,平面AEF∩平面BCD=EF,
所以BD∥EF.………………3分
因为BDÌ平面ABD,EFË平面ABD,所以EF∥平面ABD.………………6分
(2)因为AE⊥平面BCD,CDÌ平面BCD,
所以AE⊥CD.………………8分
因为BD⊥CD,BD∥EF,所以CD⊥EF,………………10分
又AE∩EF=E,AEÌ平面AEF,EFÌ平面AEF,所以CD⊥平面AEF.………………12分
又CDÌ平面ACD,所以平面AEF⊥平面ACD.………………14分
16.(本小题满分14分)
解:(1)解法1:
在△ABC中,因为cosB=,所以=.………………2分
因为c=2a,所以=,即=,所以=.………………4分
又由正弦定理得=,所以=.………………6分
解法2:
因为cosB=,B∈(0,π),所以sinB==.………………2分
因为c=2a,由正弦定理得sinC=2sinA,
所以sinC=2sin(B+C)=cosC+sinC,即-sinC=2cosC.………………4分
又因为sin2C+cos2C=1,sinC>0,解得sinC=,
所以=.………………6分
(2)因为cosB=,所以cos2B=2cos2B-1=.………………8分
又0<B<π,所以sinB==,
所以sin2B=2sinBcosB=2××=.………………10分
因为C-B=,即C=B+,所以A=π-(B+C)=-2B,
所以sinA=sin(-2B)=sincos2B-cossin2B=.………………14分
17.(本小题满分14分)
解:(1)因为扇形 AOC的半径为 40 m,∠AOC=x rad,
所以扇形AOC的面积S扇形AOC==800x,0<x<π.………………2分
在△COD中,OD=80,OC=40,∠COD=π-x,
所以S△COD=·OC·OD·sin∠COD=1600sin(π-x)=1600sinx.………………4分
从而 S=S△COD+S扇形AOC=1600sinx+800x,0<x<π.………………6分
(2)由(1)知, S(x)=1600sinx+800x,0<x<π.
S′(x)=1600cosx+800=1600(cosx+).………………8分
由 S′(x)=0,解得x=.
从而当0<x<时,S′(x)>0;当<x<π时,S′(x)<0 .
因此 S(x)在区间(0,)上单调递增;在区间(,π)上单调递减.………………11分
所以 当x=,S(x)取得最大值.
答:当∠AOC为时,改建后的绿化区域面积S最大.………………14分
18.(本小题满分16分)
解:(1)由题得且,解得
所以椭圆的方程为.………………4分
(2)设,,
①直线的方程为,代入椭圆得,
由得,,………………8分
所以.……………10分
②直线过定点,理由如下:
由题得,………………12分
由得,
则的方程为,即,………………14分
所以直线过定点.………………16分
19.(本小题满分16分)
解:(1)因为,所以,
由可得.
又因为在处取得极值,所以,
所以.………………2分
所以,其定义域为.
,
令得,当时,,当时,,
所以函数h(x)在区间上单调增,在区间上单调减.………………4分
(2)当时,,其定义域为.
①由得,记,则,
所以在单调减,在单调增,
所以当时,取得最小值.………………6分
又,所以时,,而时,,
所以b的取值范围是.………………10分
注:此处需用零点存在定理证明,如考生未证明,此问最多不超过3分.
②由题意得,
所以,
所以,………………12分
不妨设x10,若p是q
的充分不必要条件,则实数a的取值范围是 ▲ .
【点评】逻辑用语,中等题。此题为改编题。
【答案】6.[5,7]
7.等比数列{an}的前n项和为Sn,若4a1,2a2,a3成等差数列,a1=1,则S7= ▲ .
【点评】等比数列公式的考查,中等题。
【答案】7.127
8.函数f(x)是在R上的周期为3的奇函数,当0c-1的解集为(m-4,m),则实数c的值为 ▲ .
【点评】函数值域与不等式的简单综合,中等题。此题为改编题。
【答案】11.-3
12.在锐角△ABC中,已知sinC=4cosAcosB,则tanAtanB的最大值为 ▲ .
【点评】以正切为切入点的最值问题,中等题。此题有较多变式,后续教学应重点关注。
【答案】12.4
13.在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为 ▲ .
【点评】三角形中的最值问题,中等题。
【答案】13.9
14.设函数f(x)=ax+sinx+cosx.若函数f(x)的图象上存在不同的两点A,B,使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为 ▲ .
【点评】函数与导数综合,以切线为切入点,难题。此题源自南京二模。
【答案】14.[-1,1]
【填空题总评】本次考试填空题难度不大,关注基本点的考查,考生在本部分如低于60分,需要加强相关基本题的训练。此外,本次填空有多题为各市前几年的二模真题或改编题,难度略低,但考点覆盖较全面,针对近两年难度的下降,填空题难度的下降也会成为趋势。
二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)
15.(本小题满分14分)
如图,在三棱锥A-BCD中,E,F分别为棱BC,CD上的点,且BD∥平面AEF.
(1)求证:EF∥平面ABD;
(2)若BD⊥CD,AE⊥平面BCD,求证:平面AEF⊥平面ACD.
【点评】本题考查线面平行的判定定理,面面平行的判定定理,简单题。在阅卷时,应严格按照评分标准进行阅卷。对于考生在此部分答题的不规范,应严格判分。
A
B
C
F
E
D
(第15题)
【答案】
解:(1)因为BD∥平面AEF,BDÌ平面BCD,平面AEF∩平面BCD=EF,
所以BD∥EF.………………3分
因为BDÌ平面ABD,EFË平面ABD,所以EF∥平面ABD.………………6分
(2)因为AE⊥平面BCD,CDÌ平面BCD,
所以AE⊥CD.………………8分
因为BD⊥CD,BD∥EF,所以CD⊥EF,………………10分
又AE∩EF=E,AEÌ平面AEF,EFÌ平面AEF,所以CD⊥平面AEF.………………12分
又CDÌ平面ACD,所以平面AEF⊥平面ACD.………………14分
16.(本小题满分14分)
在△ABC中,内角A,B, C所对的边分别为a,b,c,cosB=.
(1)若c=2a,求的值;
(2)若C-B=,求sinA的值.
【点评】本题考查正弦定理与余弦定理,三角函数的相关运算,中等题。注意考生的答题规范。
【答案】
解:(1)解法1:
在△ABC中,因为cosB=,所以=.………………2分
因为c=2a,所以=,即=,所以=.………………4分
又由正弦定理得=,所以=.………………6分
解法2:
因为cosB=,B∈(0,π),所以sinB==.………………2分
因为c=2a,由正弦定理得sinC=2sinA,
所以sinC=2sin(B+C)=cosC+sinC,即-sinC=2cosC.………………4分
又因为sin2C+cos2C=1,sinC>0,解得sinC=,
所以=.………………6分
(2)因为cosB=,所以cos2B=2cos2B-1=.………………8分
又0<B<π,所以sinB==,
所以sin2B=2sinBcosB=2××=.………………10分
因为C-B=,即C=B+,所以A=π-(B+C)=-2B,
所以sinA=sin(-2B)=sincos2B-cossin2B=.………………14分
17.(本小题满分14分)
如图,某城市有一块半径为40 m的半圆形绿化区域(以O为圆心,AB为直径),现计划对其进行改建.在AB的延长线上取点D,OD=80 m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2.设∠AOC=x rad.
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)试问∠AOC多大时,改建后的绿化区域面积S取得最大值.
【点评】
应用题,以三角函数为基底进行考查,中等题。此题源自南京市零模,难度不大。在高考中,预测应用题也会以三角函数为基底进行考查,关注导数或不等式。
【答案】
解:(1)因为扇形 AOC的半径为 40 m,∠AOC=x rad,
所以扇形AOC的面积S扇形AOC==800x,0<x<π.………………2分
在△COD中,OD=80,OC=40,∠COD=π-x,
所以S△COD=·OC·OD·sin∠COD=1600sin(π-x)=1600sinx.………………4分
从而 S=S△COD+S扇形AOC=1600sinx+800x,0<x<π.………………6分
A
B
O
C
D
(第17题)
(2)由(1)知, S(x)=1600sinx+800x,0<x<π.
S′(x)=1600cosx+800=1600(cosx+).………………8分
由 S′(x)=0,解得x=.
从而当0<x<时,S′(x)>0;当<x<π时,S′(x)<0 .
因此 S(x)在区间(0,)上单调递增;在区间(,π)上单调递减.………………11分
所以 当x=,S(x)取得最大值.
答:当∠AOC为时,改建后的绿化区域面积S最大.………………14分
18.(本小题满分16分)
在平面直角坐标系xOy中,已知椭圆E:+=1(a>b>0)过点,其离心率等于.
(1)求椭圆E的标准方程;
(2)若A,B分别是椭圆E的左,右顶点,动点M满足MB⊥AB,且MA交椭圆E于点P.
①求证:为定值;
②设PB与以PM为直径的圆的另一交点为Q,求证:直线MQ经过定点.
【点评】本题考查解析几何,关注向量的运算,在二模中属于热度题,中等题。定点定值题,一定要算到底,注意方法优化,本题应注意一题多解。
【答案】
解:(1)由题得且,解得
所以椭圆的方程为.………………4分
(2)设,,
①直线的方程为,代入椭圆得,
由得,,………………8分
所以.……………10分
②直线过定点,理由如下:
由题得,………………12分
由得,
则的方程为,即,………………14分
所以直线过定点.………………16分
19.(本小题满分16分)
已知函数f(x)=ax2+lnx,g(x)=-bx,设h(x)=f(x)-g(x).
(1)若f(x)在x=处取得极值,且f ′(1)=g(-1)-2,求函数h(x)的单调区间;
(2)若a=0时,函数h(x)有两个不同的零点x1,x2.
①求b的取值范围;
②求证:x1·x2>e2.
【点评】本题考查函数与导数,中等题。零点问题注意零点存在定理的使用,如不使用得分会较低。第三问考查点较为基础,在教学过程中教师应注意这类题的证法。在高考中,不会再出现这样的陈题、旧题,但这样的方法与思想应该牢牢把握。
【答案】
解:(1)因为,所以,由可得.
又因为在处取得极值,所以,
所以.………………2分
所以,其定义域为.,
令得,当时,,当时,,
所以函数h(x)在区间上单调增,在区间上单调减.………………4分
(2)当时,,其定义域为.
①由得,记,则,
所以在单调减,在单调增,
所以当时,取得最小值.………………6分
又,所以时,,而时,,
所以b的取值范围是.………………10分
注:此处需用零点存在定理证明,如考生未证明,此问最多不超过3分.
②由题意得,所以,
所以,………………12分
不妨设x1
查看更多