2018届二轮复习专题三第1讲　三角函数的图象与性质课件（全国通用）

2018届二轮复习专题三第1讲　三角函数的图象与性质课件（全国通用）

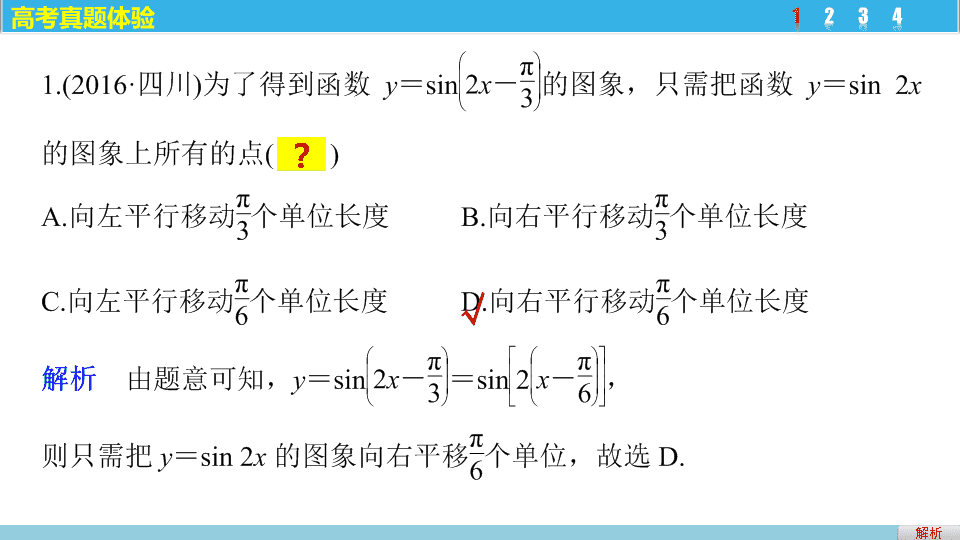
第 1 讲　 三角函数 的图象与性质 专题三　三角函数、解三角形与平面向量 栏目索引 高考 真题体验 1 热点 分类突破 2 高考 押题精练 3 解析 高考真题 体验 1 2 3 4 √ 解析 1 2 3 4 √ A.11 B.9 C.7 D.5 解析 1 2 3 4 √ 1 2 3 4 所以 ω ＝ 4 k ＋ 1( k ∈ N ) ， 由此得 ω 的最大值为 9 ，故选 B. 1 2 3 4 4.(2016· 江苏 ) 定义在区间 [ 0,3π ] 上的函数 y ＝ sin 2 x 的图象与 y ＝ cos x 的图象的交点个数是 ________. 解析　 在区间 [ 0,3π ] 上分别作出 y ＝ sin 2 x 和 y ＝ cos x 的简图如下： 由图象可得两图象有 7 个交点 . 7 解析答案 考情考向分 析 返回 1. 以图象为载体，考查三角函数的最值、单调性、对称性、周期性 . 2. 考查三角函数式的化简、三角函数的图象和性质、角的求值，重点考查分析、处理问题的能力，是高考的必考点 . 热点一　三角函数的概念、诱导公式及同角关系式 热点分类突破 √ 解析　 设 Q 点的坐标为 ( x ， y ) ， 解析 (2)(2015· 四川 ) 已知 sin α ＋ 2cos α ＝ 0 ，则 2sin α cos α － cos 2 α 的值是 ________. 解析　 ∵ sin α ＋ 2cos α ＝ 0 ， ∴ sin α ＝－ 2cos α ， ∴ tan α ＝－ 2 ， － 1 解析答案 思维升华 思维 升华 (1) 涉及与圆及角有关的函数建模问题 ( 如钟表、摩天轮、水车等 ) ，常常借助三角函数的定义求解 . 应用定义时，注意三角函数值仅与终边位置有关，与终边上点的位置无关 . (2) 应用诱导公式时要弄清三角函数在各个象限内的符号；利用同角三角函数的关系化简过程要遵循一定的原则，如切化弦、化异为同、化高为低、化繁为简等 . √ 解析 解析答案 热点二　三角函数的图象及应用 函数 y ＝ A sin( ωx ＋ φ ) 的图象 (1) “ 五点法 ” 作图： (2) 图象变换： 点、连线可得 . √ 解析 1 答案 解析 思维升华 思维升华 思维 升华 (1) 已知函数 y ＝ A sin( ωx ＋ φ )( A >0 ， ω >0) 的图象求解析式时，常采用待定系数法，由图中的最高点、最低点或特殊点求 A ；由函数的周期确定 ω ；确定 φ 常根据 “ 五点法 ” 中的五个点求解，其中一般把第一个零点作为突破口，可以从图象的升降找准第一个零点的位置 . (2) 在图象变换过程中务必分清是先相位变换，还是先周期变换 . 变换只是相对于其中的自变量 x 而言的，如果 x 的系数不是 1 ，就要把这个系数提取后再确定变换的单位长度和方向 . √ 解析 解析　 由题意知，函数 f ( x ) 的周期 T ＝ π ， 即可得到 g ( x ) ＝ cos 2 x 的图象 . 故选 A. A.5 B.6 C.8 D.10 √ 解析　 由题干图易得 y min ＝ k － 3 ＝ 2 ，则 k ＝ 5. ∴ y max ＝ k ＋ 3 ＝ 8. 解析 热点三　三角函数的性质 1. 三角函数的单调区间： 2. y ＝ A sin( ωx ＋ φ ) ，当 φ ＝ k π( k ∈ Z ) 时为奇函数； 当 φ ＝ k π( k ∈ Z ) 时为偶函数；对称轴方程可由 ωx ＋ φ ＝ k π( k ∈ Z ) 求得 . y ＝ A tan( ωx ＋ φ ) ，当 φ ＝ k π( k ∈ Z ) 时为奇函数 . (1) 求 f ( x ) 的最小正周期和最大值； 解析答案 解析答案 思维升华 思维 升华 函数 y ＝ A sin( ωx ＋ φ ) 的性质及应用的求解思路 第一步：先借助三角恒等变换及相应三角函数公式把待求函数化成 y ＝ A sin( ωx ＋ φ ) ＋ B 的形式； 第二步：把 “ ωx ＋ φ ” 视为一个整体，借助复合函数性质求 y ＝ A sin( ωx ＋ φ ) ＋ B 的单调性及奇偶性、最值、对称性等问题 . 跟踪演练 3 　 设函数 f ( x ) ＝ 2cos 2 x ＋ sin 2 x ＋ a ( a ∈ R ). (1) 求函数 f ( x ) 的最小正周期和单调递增区间； 解析答案 返回 解析答案 1 2 3 解析 押题依据 高考押题精练 押题依据　 本题结合函数图象的性质确定函数解析式，然后考查图象的平移，很有代表性，考生应熟练掌握图象平移规则，防止出错 . √ 1 2 3 解析　 先求出周期确定 ω ，求出两个函数解析式，然后结合平移法则求解 . 则其最小正周期 T ＝ π ， 1 2 3 解析 押题依据 √ 押题依据　 由三角函数的图象求解析式是高考的热点，本题结合平面几何知识求 A ，考查了数形结合思想 . 1 2 3 解析　 由题意设 Q ( a, 0) ， R (0 ，－ a )( a >0). 1 2 3 押题依据 (1) 求函数 f ( x ) 的解析式及其图象的对称轴方程； (2) 将函数 y ＝ f ( x ) 的图象向右平移 2 个单位后得到函数 y ＝ g ( x ) 的图象，当 x ∈ ( － 1,2] 时，求函数 h ( x ) ＝ f ( x )· g ( x ) 的值域 . 返回 解析答案 1 2 3 押题依据　 三角函数解答题的第 (1) 问的常见形式是求周期、求单调区间及求对称轴方程 ( 或对称中心 ) 等，这些都可以由三角函数解析式直接得到，因此此类命题的基本方式是利用三角恒等变换得到函数的解析式 . 第 (2) 问的常见形式是求解函数的值域 ( 或最值 ) ，特别是指定区间上的值域 ( 或最值 ) ，是高考考查三角函数图象与性质命题的基本模式 . 解析答案 1 2 3 由题意知 f ( x ) 的最小正周期为 12 ， 又 a >0 ，所以 a ＝ 1 . 于是 所求函数的解析式为 即函数 f ( x ) 图象的对称轴方程为 x ＝ 1 ＋ 6 k ( k ∈ Z ). 解析答案 1 2 3 于是函数 h ( x ) 的值域为 ( － 1,3]. 返回