2020届二轮复习第三课时概率的基本性质课件（10张）（全国通用）

2020届二轮复习第三课时概率的基本性质课件（10张）（全国通用）

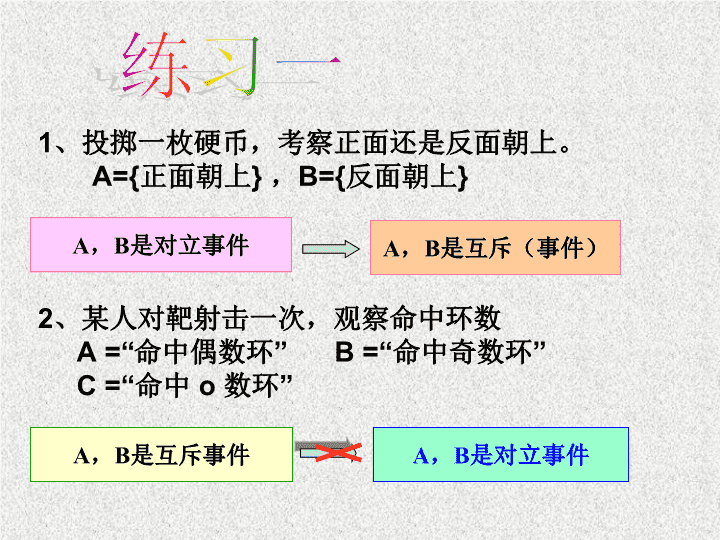
在掷骰子试验中，可以定义许多事件，例如： C 1 = ｛出现 1 点｝ ,C 2 = ｛出现 2 点｝ ,C 3 = ｛出现 3 点｝， C 4 = ｛出现 4 点｝ ,C 5 = ｛出现 5 点｝ ,C 6 = ｛出现 6 点｝， D 1 = ｛出现的点数不大于 1 ｝， D 2 = ｛出现的点数大于 3 ｝， D 3 = ｛出现的点数小于 5 ｝， E= ｛出现的点数小于 2 ｝， F= ｛出现的点数大于 4 ｝， G= ｛出现的点数为偶数｝， H= ｛出现的点数为奇数｝。 …… A∩B=Φ 其含义是：事件 A 与 B 在任何一次试验中不会同时发生。 互斥事件 对立事件 A∩B=Φ A∪B=Ω 其含义是：事件 A 与事件 B 在任何 一次试验中有且只有一个发生。 ( 一 ) 、事件的关系和运算 1 、投掷一枚硬币，考察正面还是反面朝上。 A={ 正面朝上 } ， B={ 反面朝上 } 练习一 A ， B 是对立事件 A ， B 是互斥（事件） 2 、某人对靶射击一次，观察命中环数 A =“ 命中偶数环” B =“ 命中奇数环” C =“ 命中 o 数环” A ， B 是互斥事件 A ， B 是对立事件 练习二 3 、一名学生独立解答两道物理习题，考察这两道 习题的解答情况。 记 A = “ 该学生会解答第一题，不会解答第二题” B = “ 该学生会解答第一题，还会解答第二题” 试回答： 1. 事件 A 与 事件 B 互斥吗？为什么？ 2. 事件 A 与 事件 B 互为对立事件吗？为什么？ 4 、 某检查员从一批产品中抽取 8 件进行检查，观察其中的次品数 记： A =“ 次品数少于 5 件” ; B = “ 次品数恰有 2 件” C = “ 次品数多于 3 件” ; D = “ 次品数至少有 1 件” 试写出下列事件的基本事件组成： A∪B ， A∩C, B∩C ; 练习三 A∪B = A ( A,B 中至少有一个发生 ） A∩C= “ 有 4 件次品” B∩C = 1. 概率 P ( A ) 的取值范围 （ 1 ） 0≤ P ( A )≤1. （ 2 ）必然事件的概率是 1. （ 3 ）不可能事件的概率是 0. （ 4 ）若 A B,P(A) 与 P(B) 会有什么关系呢 ? ( 二 ) 、概率的几个基本性质 若 A B, 则 p(A) ≤ P(B) 思考： 掷一枚骰子 , 事件 C 1 ={ 出现 1 点 } ，事件 C 3 ={ 出现 3 点 } 则事件 C 1  C 3 发生的频率 与事件 C 1 和事件 C 3 发生的频率之间有什 么关系 ? 结论： 当事件 A 与事件 B 互斥时 2. 概率的加法公式： 如果 事件 A 与事件 B 互斥 ，则 P ( A  B ） = P ( A ) + P ( B ） 若 事件 A ， B 为对立事件 , 则 P ( A ) +P ( B ） =1 或者 3. 对立事件的概率公式 P ( B ） =1 － P ( A ) （ 1 ） 取到红色牌（ 事件 C ）的概率是多少？ （ 2 ） 取到黑色牌（ 事件 D ）的概率是多少？   例 2 、 如果从不包括大小王的 52 张扑克牌中随机抽取一张，那么取到红心（ 事件 A ）的概率是 ，取到方片（ 事件 B ）的概率是 。问 : 解 : 所以 A 与 B 是互斥事件。 因为 C= A  B ， 根据概率的加法公式， 且 A 与 B 不会同时发生， (1) P ( A )+ P （ B ） 得 P （ C ） = 所以 所以 C 与 D 为对立事件。 C 与 D 是互斥事件， 又因为 C  D 为必然事件， （ 2 ） 1 － P (C) P （ D ） = 1 、事件的关系与运算，区分 互斥事件与对立事件 本 课 小 结 事件 关系 1. 包含关系 2. 等价关系 事件 运算 3. 事件的并 ( 或和 ) 4. 事件的交 ( 或积 ) 5. 事件的互斥 ( 或互不相容 ) 6. 对立事件 ( 逆事件 )