2018-2019学年山西省应县第一中学校高一上学期期末考试数学试题

2018-2019学年山西省应县第一中学校高一上学期期末考试数学试题

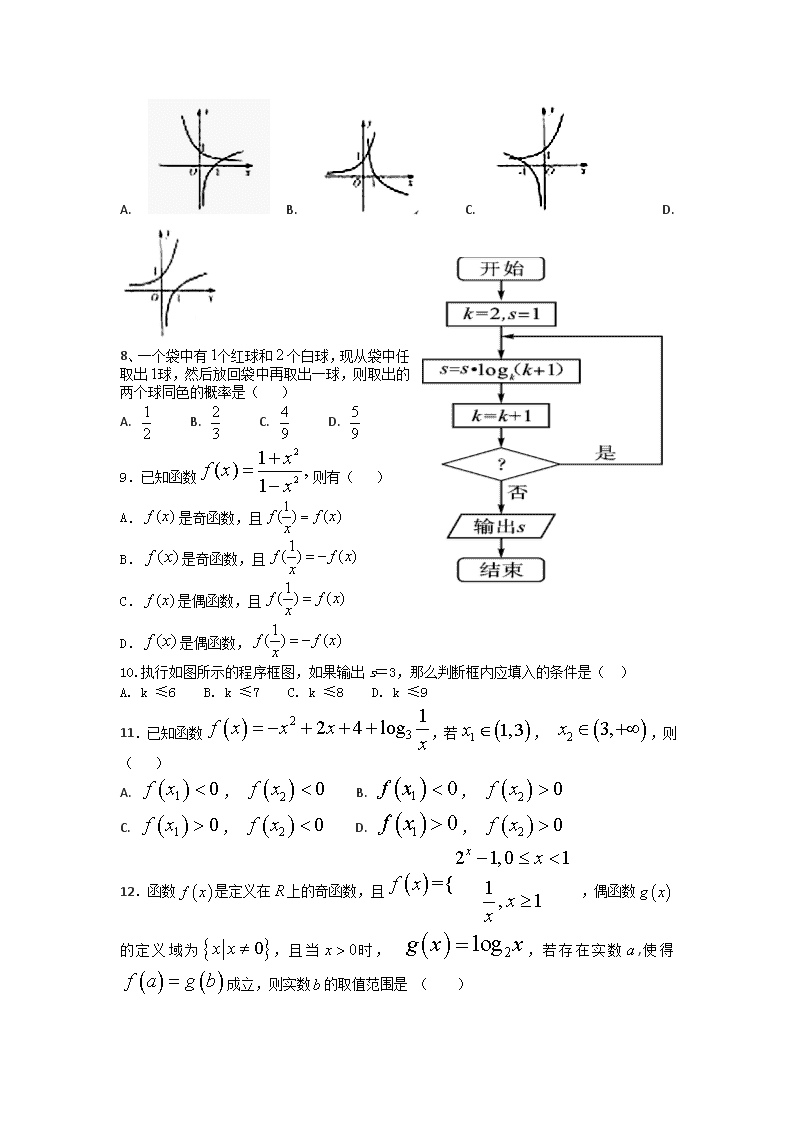
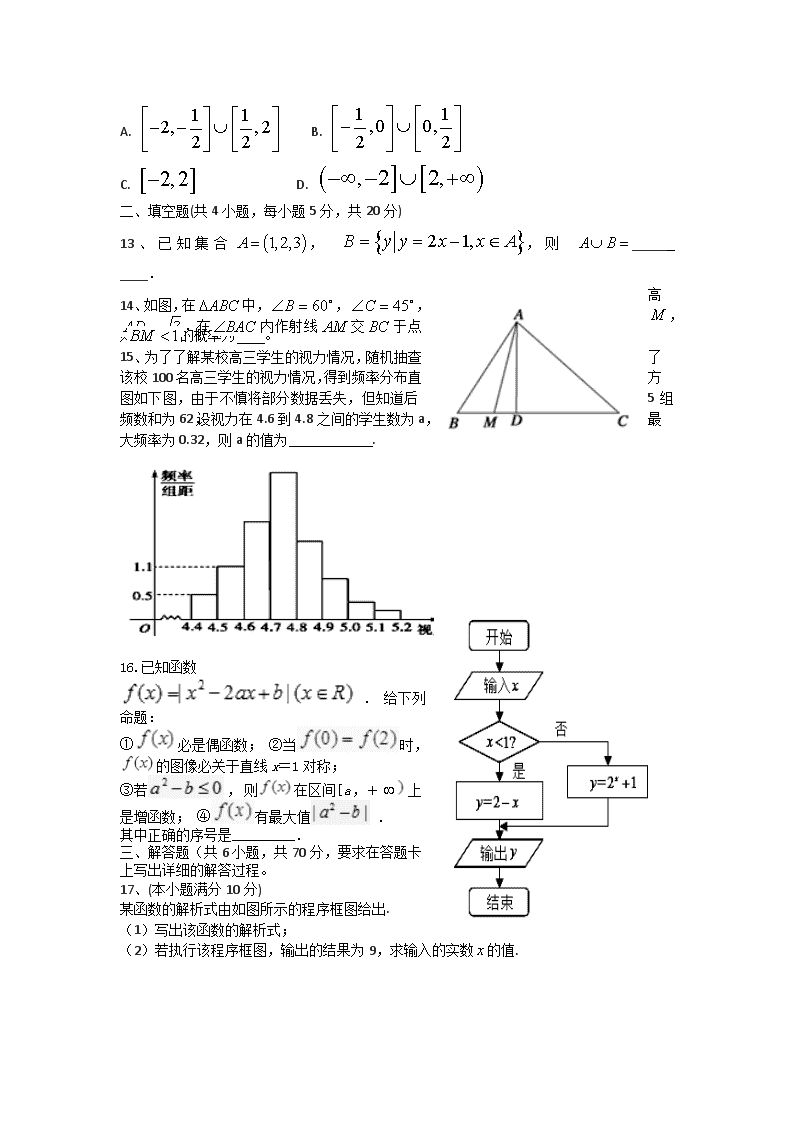
‎2018-2019学年山西省应县第一中学校高一上学期期末考试数学试题 时间：120分钟 满分：150分 一、 选择题：(本大题共12小题，每小题5分，共60分，每小题给出的四个选项，只有一项是符合题目要求的).‎ ‎1. 已知集合，，则（ ）‎ A. B. C. D. ‎ ‎2．下列语句正确的是（ ）‎ A. B. C. D. ‎ ‎3. 将红、黑、蓝、白5张纸牌（其中白纸牌有2张）随机分发给甲、乙、丙、丁4个人，每人至少分得1张，则下列两个事件为互斥事件的是（ ）‎ A. 事件“甲分得1张白牌”与事件“乙分得1张红牌” ‎ B. 事件“甲分得1张红牌”与事件“乙分得1张蓝牌”‎ C. 事件“甲分得1张白牌”与事件“乙分得2张白牌”‎ D. 事件“甲分得2张白牌”与事件“乙分得1张黑牌”‎ ‎4.执行如图所示的程序框图，输出的s值为（ 　）‎ A. -3 B.- C. D. 2‎ ‎5. 若函数满足，且，，则（ ）‎ A. 1 B. 3 C. D. ‎ ‎6、已知在矩形中，AB=5，BC=7，在其中任取一点P，使满足，则P点出现的概率为 （ ）‎ A. B. C. D. 不确定 ‎7．已知，则函数与函数的图象可能是 （ ）‎ A. B. C. D. ‎ ‎8、一个袋中有个红球和个白球，现从袋中任取出球，然后放回袋中再取出一球，则取出的两个球同色的概率是（ ）‎ A. B. C. D. ‎ ‎9．已知函数则有（ ）‎ A．是奇函数，且 ‎ B．是奇函数，且 C．是偶函数，且 ‎ D．是偶函数，‎ ‎10.执行如图所示的程序框图，如果输出s＝3，那么判断框内应填入的条件是（ ）‎ A. k ≤6 B. k ≤7 C. k ≤8 D. k ≤9‎ ‎11．已知函数，若， ，则（ ）‎ A. ， B. ， ‎ C. ， D. ， ‎ ‎12．函数是定义在上的奇函数，且，偶函数的定义域为，且当时， ，若存在实数,使得成立，则实数的取值范围是 （ ）‎ A. B. ‎ C. D. ‎ 二、填空题(共4小题，每小题5分，共20分)‎ ‎13、已知集合， ，则 ______ ____．‎ ‎14、如图，在中，，，高，在内作射线交于点，则的概率为 。‎ ‎15、为了了解某校高三学生的视力情况，随机抽查了该校100名高三学生的视力情况，得到频率分布直方图如下图，由于不慎将部分数据丢失，但知道后5组频数和为62，设视力在4.6到4.8之间的学生数为a，最大频率为0.32，则a的值为 .‎ ‎16.已知函数 ． 给下列命题： ①必是偶函数； ②当时，的图像必关于直线x＝1对称； ③若 ， 则在区间[a ，＋上是增函数； ④有最大值 ． 其中正确的序号是_________．‎ 三、解答题（共6小题，共70分，要求在答题卡上写出详细的解答过程。‎ ‎17、(本小题满分10分)‎ 某函数的解析式由如图所示的程序框图给出.‎ ‎（1）写出该函数的解析式；‎ ‎（2）若执行该程序框图，输出的结果为9，求输入的实数的值.‎ ‎18、(本小题满分12分)‎ 如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数, 乙组记录中有一个数据模糊，无法确认, 在图中以表示.‎ ‎（1）如果乙组同学投篮命中次数的平均数为, ‎ 求及乙组同学投篮命中次数的方差; ‎ ‎（2）在（1）的条件下, 分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名, 记事件A：“两名同学的投篮命中次数之和为17”, 求事件A发生的概率.‎ ‎19．(本小题满分12分)‎ 某市统计局就某地居民的月收入调查了10000人,他们的月收入均在内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在内) ‎ ‎(1)求某居民月收入在内的频率； ‎ ‎(2)根据该频率分布直方图估计居民的月收入的中位数；‎ ‎(3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在内的居民中抽取多少人?‎ ‎20.(本小题满分12分) 已知函数（且）.‎ ‎（1）当时，，‎ 求的取值范围；‎ ‎（2）若在上的最小值大于1，求a的取值范围.‎ ‎21、(本小题满分12分)已知集合 ‎（1）若，求的概率； ‎ ‎（2）若，求的概率.‎ ‎22.(本题满分12分)已知函数f(x)＝log4(4x＋1)＋( ∈R)是偶函数．‎ ‎(1)求实数k的值；‎ ‎(2)设g(x)＝log4(a·2x＋a)，若f(x)＝g(x)有且只有一个实数解，求实数a的取值范围。‎ 高一期末数学答案2019.1‎ 一、 选择题：(本大题共12小题，每小题5分，共60分，每小题给出的四个选项，只有一项是符合题目要求的).‎ ‎1-6 DBCDBA 7-12 DDDBCA ‎ 二、填空题(共4小题，每小题5分，共20分)‎ ‎13. 14. 15. 54 16. ③ ‎ 三、解答题（共6小题，共70分，要求在答题卡上写出详细的解答过程。‎ 17． ‎(本小题满分10分)‎ 答案：（1）；（2）或3.‎ 解：（1）.‎ ‎（2）当时， ， ；‎ 当时， ， ， 所以或3.‎ 18、 ‎(本小题满分12分)‎ ‎【答案】（1），；（2）.‎ 解：（Ⅰ）由题可得，‎ 方差 ‎（Ⅱ）记甲组投篮命中次数低于10次的同学为，他们的投篮命中次数分别为9,7‎ 记乙组投篮命中次数低于10次的同学，他们的投篮命中次数分别为8，8,9，由题意 不同的选取方法有共6种，‎ 设“这两名同学的投篮命中次数之和为17”为事件，则中含有共2种基本事件 故 ‎19、(本小题满分12分)‎ 解：(1) 由频率分布直方图可知，居民月收入在内的频率为：‎ ‎(0.0002+0.0003)×500=0. 25．       ……………………2分 (2) 由频率分布直方图可知 0.0001×500=0.05, 0.0004×500=0.20, 0.0005×500=0.25, 从而有0.0001×500+0.0004×500+0.0005×500="0.5,"  ……………………6分 所以可以估计居民的月收入的中位数为2500(元)．   ………………‎ ‎7分 (3) 由频率分布直方图可知，居民月收入在内的频率为 0.0003×500=0.15,                  ……………………9分 所以这10000人中月收入在内的人数为0.15×10000=1500(人),  ……………………11分 再从这10000人中利用分层抽样的方法抽取100人,则应从月收入在内的居民中抽取(人).             ……………………12分 ‎ ‎20、(本小题满分12分)‎ ‎【答案】（1）；（2）.‎ 解：（1）当时，， ，得.‎ ‎（2）在定义域内单调递减，‎ 当时，函数在上单调递减，，得.‎ 当时，函数在上单调递增，，不成立.‎ 综上：.‎ 21、 ‎(本小题满分12分)‎ ‎【答案】（1）(2)‎ 解：（1）设为事件，，‎ 即，即.‎ 则基本事件有：共个，其中满足的基本事件有个，所以.故的概率为.‎ ‎(2)设为事件，因为，则基本事件为如图四边形区域，事件包括的区域为其中的阴影部分.‎ 所以，‎ 故的概率为.‎ ‎22、(本小题满分12分)‎ 解：(1)由函数f(x)是偶函数可知f(x)＝f(－x)，‎ ‎∴log4(4x＋1)＋kx＝log4(4－x＋1)－kx，‎ 化简得log4＝－2kx，‎ 即x＝－2kx对一切x∈R恒成立，∴ k＝－...................4分 ‎(2)函数f(x)与g(x)的图象有且只有一个公共点，‎ 即方程log4(4x＋1)－x＝log4(a·2x＋a)有且只有一个实根，‎ 化简得方程2x＋＝a·2x＋a有且只有一个实根，且a·2x＋a>0成立，则a>0........6分 令t＝2x>0，则(a－1)t2＋at－1＝0有且只有一个正根．‎ 设g(t)＝(a－1)t2＋at－1，注意到g(0)＝－1<0，所以 ‎①当a＝1时，有t＝1，符合题意；…………………………7分 ‎②当01时，又g(0)＝－1，方程恒有一个正根与一个负根，符合题意．……10分 综上可知， a的取值范围是{－2＋2}∪1，＋∞)．…………12分 ‎ ‎