2019高三数学文北师大版一轮课时分层训练36+简单几何体的结构、三视图和直观图

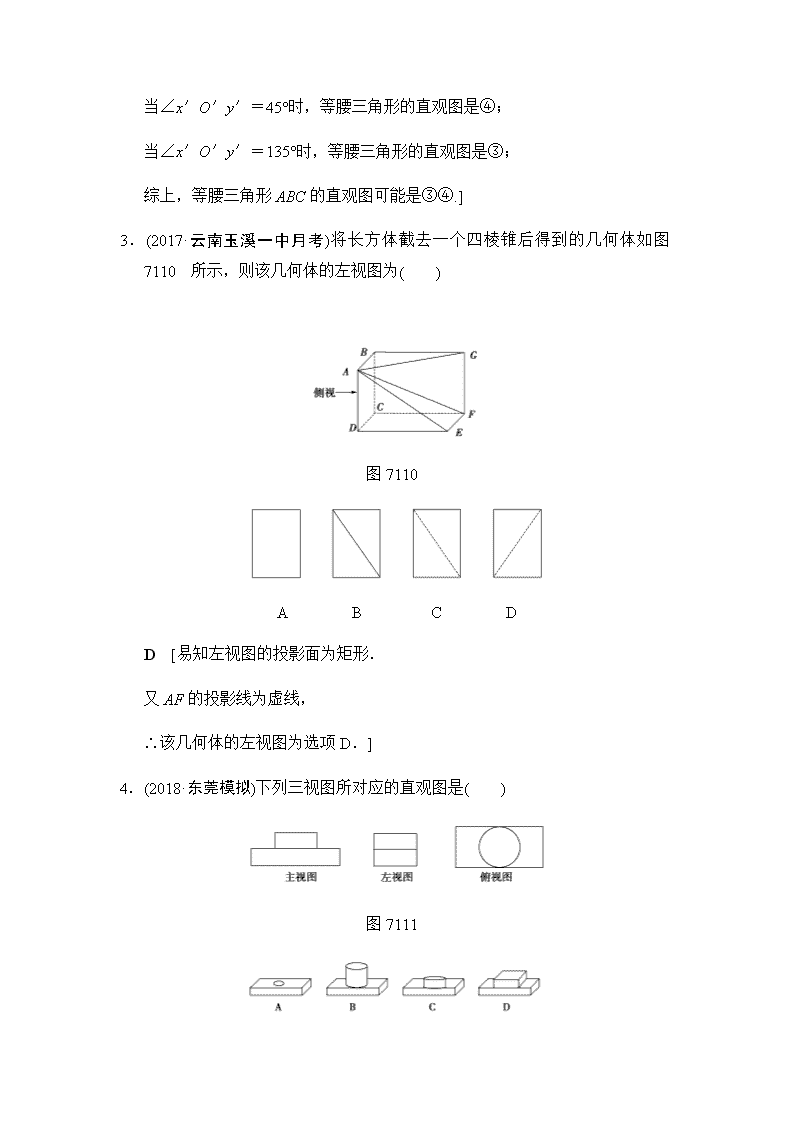
2019高三数学文北师大版一轮课时分层训练36+简单几何体的结构、三视图和直观图

课时分层训练(三十六)　‎ 简单几何体的结构、三视图和直观图 ‎ (对应学生用书第250页)‎ A组　基础达标 ‎(建议用时：30分钟)‎ 一、选择题 ‎1．关于简单几何体的结构特征，下列说法不正确的是(　　)‎ A．棱柱的侧棱长都相等 B．棱锥的侧棱长都相等 C．三棱台的上、下底面是相似三角形 D．有的棱台的侧棱长都相等 B　[根据棱锥的结构特征知，棱锥的侧棱长不一定都相等．]‎ ‎2．(2018·石家庄模拟)等腰三角形ABC的直观图是(　　) 【导学号：00090229】‎ 图719‎ A．①②　 B．②③‎ C．②④ D．③④‎ D　[由直观图画法可知，‎ 当∠x′O′y′＝45°时，等腰三角形的直观图是④；‎ 当∠x′O′y′＝135°时，等腰三角形的直观图是③；‎ 综上，等腰三角形ABC的直观图可能是③④.]‎ ‎3．(2017·云南玉溪一中月考)将长方体截去一个四棱锥后得到的几何体如图7110所示，则该几何体的左视图为(　　)‎ 图7110‎ A　　　　B　　　 　C　　　　D D　[易知左视图的投影面为矩形．‎ 又AF的投影线为虚线，‎ ‎∴该几何体的左视图为选项D．]‎ ‎4．(2018·东莞模拟)下列三视图所对应的直观图是(　　)‎ 图7111‎ C　[由题意可知，几何体的直观图下部是长方体，上部是圆柱，并且高相等，应选C．]‎ ‎5．(2015·全国卷Ⅱ)一个正方体被一个平面截去一部分后，剩余部分的三视图如图7112，则截去部分体积与剩余部分体积的比值为(　　)‎ 图7112‎ A． B． C． D． D　[由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分，如图所示，截去部分是一个三棱锥．设正方体的棱长为1，则三棱锥的体积为 V1＝××1×1×1＝，‎ 剩余部分的体积V2＝13－＝.‎ 所以＝＝，故选D．]‎ 二、填空题 ‎6．(2017·福建龙岩联考)一水平放置的平面四边形OABC，用斜二测画法画出它的直观图O′A′B′C′如图7113所示，此直观图恰好是一个边长为1的正方形，则原平面四边形OABC的面积为________．‎ 图7113‎ ‎2　[因为直观图的面积是原图形面积的倍，且直观图的面积为1，所以原图形的面积为2.]‎ ‎7．如图7114所示，在正方体ABCDA1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥PABC的主视图与左视图的面积的比值为________．‎ 图7114‎ ‎1　[三棱锥PABC的主视图与左视图为底边和高均相等的三角形，故它们的面积相等，面积比值为1.]‎ ‎8．某三棱锥的三视图如图7115所示，则该三棱锥最长棱的棱长为________. 【导学号：00090230】‎ 图7115‎ ‎2　‎ ‎[由题中三视图可知，三棱锥的直观图如图所示，其中PA⊥平面ABC，M为AC的中点，且BM⊥AC，故该三棱锥的最长棱为PC．‎ 在Rt△PAC中，‎ PC＝＝＝2.]‎ 三、解答题 ‎9．某几何体的三视图如图7116所示．‎ 图7116‎ ‎(1)判断该几何体是什么几何体？‎ ‎(2)画出该几何体的直观图．‎ ‎[解]　(1)该几何体是一个正方体切掉两个圆柱后的几何体．‎ ‎(2)直观图如图所示．‎ ‎10．如图7117①，在四棱锥PABCD中，底面为正方形，PC与底面ABCD垂直，如图7117②为该四棱锥的主视图和左视图，它们是腰长为6 cm的全等的等腰直角三角形．‎ 图7117①‎ 图7117①‎ ‎(1)根据图中所给的主视图、左视图，画出相应的俯视图，并求出该俯视图的面积；‎ ‎ (2)求PA． 【导学号：00090231】‎ ‎[解]　(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形，如图，其面积为36 cm2.‎ ‎(2)由左视图可求得PD＝＝＝6.‎ 由主视图可知AD＝6，且AD⊥PD，‎ 所以在Rt△APD中，PA＝＝ ‎＝6 cm.‎ B组　能力提升 ‎(建议用时：15分钟)‎ ‎1．在如图7118所示的空间直角坐标系Oxyz中，一个四面体的顶点坐标分别是(0,0,2)，(2,2,0)，(1,2,1)，(2,2,2)，给出编号①②③④的四个图，则该四面体的主视图和俯视图分别为(　　)‎ 图7118‎ A．①和② B．③和①‎ C．④和③ D．④和②‎ D　[如图，在坐标系中标出已知的四个点，根据三视图的画图规则判断三棱锥的主视图为④，俯视图为②.‎ ‎]‎ ‎2．(2017·长郡中学质检)如图7119是一个几何体的三视图，则该几何体任意两个顶点间距离的最大值是(　　)‎ 图7119‎ A．4 B．5‎ C．3 D．3 D　[由三视图作出几何体的直观图(如图所示)，计算可知AF最长，且AF＝＝3.]‎ ‎3．(2018·长春模拟)三棱锥SABC及其三视图中的主视图和左视图如图7120所示，则棱SB的长为________．‎ ‎ 【导学号：00090232】‎ 图7120‎ ‎4　[由已知中的三视图可得SC⊥平面ABC，‎ 且底面△ABC为等腰三角形，在△ABC中AC＝4，AC边上的高为2，‎ 故BC＝4，在Rt△SBC中，由SC＝4，可得SB＝4.]‎