七年级上册数学课件《有理数的除法》 人教新课标 (8)

七年级上册数学课件《有理数的除法》 人教新课标 (8)

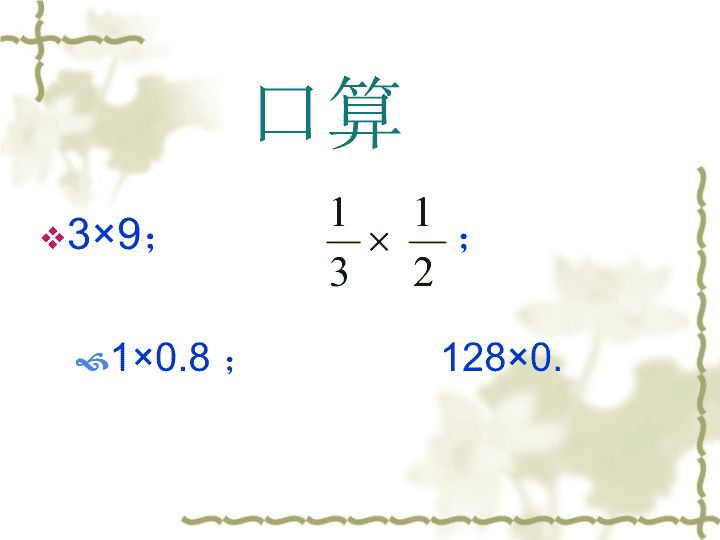
1.4有理数的乘除法 口算 v3×9； ； ›1×0.8 ； 128×0. 2 1 3 1  问题的提出 v一只小虫，沿一条东西巷的跑道，以每分钟2 米的速度向东爬行3分钟，那么它现在位于原 来位置的哪个方向？相距多少米？ 说明：若规定向东 为正，向西为负 我的解释： v这个问题用乘法来解答为： n2×3=6 n即小虫位于原来位置的东方6米处 能用数 轴表示 这一事 实么？ 动手画 一画吧。 （1）（+2）×（+3） v 0 2 4 6 2 6 东 即说明小虫向东移动了６米 问题提出2 v一只小虫，沿一条东西巷的跑道，以每分钟2 米的速度向西爬行3分钟，那么它现在位于原 来位置的哪个方向？相距多少米？ 请你也用算式和数轴的方式予以解答 (2) (-2) ×(+3) -6 -4 -2 0 -2 -6 即说明小虫在原来位置的西6米处 东 （3） （+2）×（-3） -6 -4 -2 0 2 2 -6 东 结果：向西运动6米 （4）（-2）×（-3） -2 0 2 4 6 -2 6 东 结果：向东运动6米 （５）两个数相乘，其中有一个数是 ０时，结果仍在原处． 仔细观察： v（１）　２×３＝６； v（２）　（－２）×３＝－６； v（３）　２ ×（－３）＝－６； v（４）　（－２） ×（－３）＝６； v（５）　两个数相乘，其中有一个数是０时， 积是０． 得出有理数乘法法则： 我们可以从两数的符号变化来探究积的符号变化，并决 定乘得的最后数值结果。 有理数乘法法则： 感受法则、理解法则： v 有理数乘法法则也秉承了有理数加减的探究思路，即将问题 予以归类处理，分类计算，这样有助于我们问题的解决。 v例如计算（-７）×（-４） 一，是同号相乘，所乘得的结果应为正。 二，可以先得到（-７）×（-４）= +（ ）的判断 三，把绝对值相乘，得出结果。 所以有 （-７）×（-４） =+（２８）　 的 结果 感受法则、理解法则： v再例如计算（-７）×4 一，是异号相乘，所乘得的结果应为负。 二，可以先得到（-７）× 4 = -（ ） 的判断 三，把绝对值相乘，得出结果。 所以有 （-７）×４= -（２８） 的结果 感受法则、理解法则 v若均用 或 表示是两种符号 v的数相乘的话，请判断下面几种图形相 乘所得到的图形结果。 + - + -× = + + +- - - × × × = = = - + - + 例题学习 v计算： v ①（-３）×（-９）； ②（-　）× 2 1 3 1 ③７×（-１）； ④　（-０.８）×１． ； 例题学习 v计算： v ①（-３）×（-９）； ②（-　）× 解：① （-３）×（-９） （ ３×９）=２７ 2 1 3 1 ③７×（-１）； ④　（-０.８）×１． ； ② 3 1) 2 1(  = ) 3 1 2 1(  = 6 1  ③ 7×(-1)= (7 ×1) =-7 ④　（-０.８）×１= (0.8 ×1)- =-0.8 - =+ 2.口算： v①6 × (-9) = ②(-6) ×(-9) = v③(-6) ×9= ④(-6) ×1= v⑤(-6) ×(-1) = ⑥6 ×(-1) = v⑦(-6) ×0 = ⑧0×(-6)= -54 -54 6 0 54 -6 -6 0 课堂练习（正误辨析） v你能看出下面计算有误么？ 计算： )2() 4 1(  解：原式= )2 4 1(  = 2 1  这个解答正确么？ 你认为应该怎么 做？答案是多少 呢？ - - 课堂练习（选择题） 1）如果a×b=0，则这两个数 （ ） A 都等于0， B 有一个等于0，另一个不等于0； C 至少有一个等于0， D 互为相反数 2）已知-3a是一个负数，则 （ ） A a>0 B a<0 C a≥0 D a≤0 C A 课堂练习 3）两个有理数和为0，积为负，则这两个数 的关系是 （ ） A 两个数均为0， B 两个数中一个为0 C 两数互为相反数， D 两数互为相反数，但不为0。 D