2017-2018学年江西省崇仁县第二中学高二上学期第一次月考数学（文）试题（解析版）

2017-2018学年江西省崇仁县第二中学高二上学期第一次月考数学（文）试题（解析版）

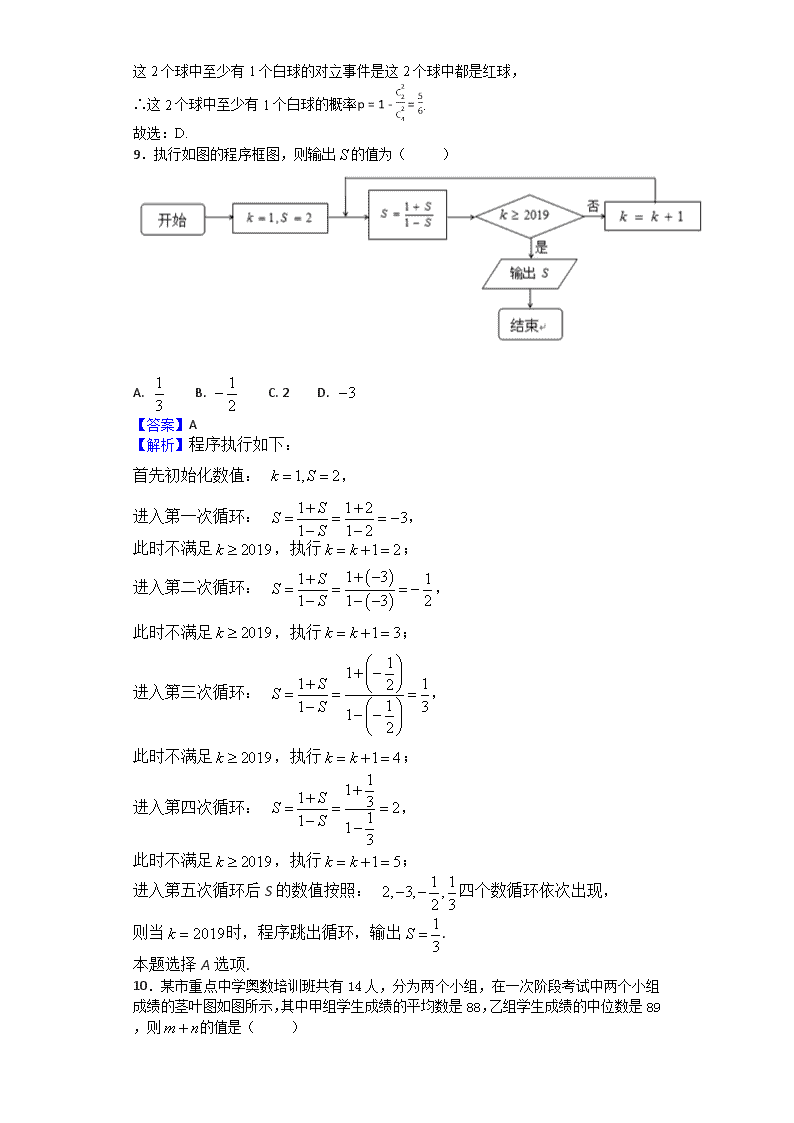
‎2017-2018学年江西省崇仁县第二中学高二上学期第一次月考数学（文）试题 一、单选题 ‎1．一个人投篮时连续投两次，则事件“至多投中一次”的互斥事件是（ ）‎ A. 只有一次投中 B. 两次都投中 C. 两次都不中 D. 至少投中一次 ‎【答案】B ‎【解析】事件“至多投中一次”包括“投中一次”和“一次也没有投中”，‎ 则该事件的互斥事件为：“两次都投中”.‎ 本题选择B选项.‎ ‎2．已知角α的终边上一点P（-4,3），则cosα=（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由题意可得： ，‎ 结合三角函数的定义可得： .‎ 本题选择D选项.‎ ‎3．某工厂采用系统抽样方法，从一车间全体300名职工中抽取20名职工进行一项安全生产调查，现将300名职工从1到300进行编号，已知从31到45这15个编号中抽到的编号是36，则在1到15中随机抽到的编号应是（ ）‎ A. 4 B. 5 C. 6 D. 7‎ ‎【答案】C ‎【解析】某工厂采用系统抽样方法，从一车间全体300名职工中抽取20名职工进行一项安全生产调查，‎ ‎∴抽样间隔为：，‎ 现将300名职工从1到300进行编号，‎ 从31到45这15个编号中抽到的编号是36，‎ 则在1到15中随机抽到的编号应是：36−15×2=6.‎ 故选：C.‎ ‎4．记为等差数列的前项和．若， ，则的公差为（ ）‎ A. 2 B. 4 C. 6 D. 8‎ ‎【答案】A ‎【解析】由题意结合等差数列的性质可得： ，‎ 则： ，‎ 从而有： .‎ 本题选择A选项.‎ ‎5．已知空间两条不同的直线和两个不同的平面，以下能推出“”的是（ ）‎ A. ， ， B. ， ， ‎ C. ， ， D. ， ， ‎ ‎【答案】C ‎【解析】对于A，平面α，β可能平行或者相交但是不一定垂直；故A错误；‎ 对于B,由m∥n,m⊥α得到n⊥α,又n⊥β,所以α∥β，得不到α⊥β；故B错误 对于D，m⊥n，m⊥α，α∩β=n，由此无法得到m与β的位置关系，因此α，β不一定垂直；故D错误；‎ ‎ 对于C,由m∥n，m⊥α得到n⊥α，又n⊂β，所以α⊥β，故C正确；‎ 本题选择C选项.‎ ‎6．圆心为且过原点的圆的标准方程是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】由题意可得，圆的半径为： ，‎ 据此可得，圆的标准方程为： .‎ 本题选择D选项.‎ 点睛：求圆的方程，主要有两种方法：‎ ‎(1)几何法：具体过程中要用到初中有关圆的一些常用性质和定理．如：①圆心在过切点且与切线垂直的直线上；②圆心在任意弦的中垂线上；③两圆相切时，切点与两圆心三点共线．‎ ‎(2)待定系数法：根据条件设出圆的方程，再由题目给出的条件，列出等式，求出相关量．一般地，与圆心和半径有关，选择标准式，否则，选择一般式．不论是哪种形式，都要确定三个独立参数，所以应该有三个独立等式．‎ ‎7．的内角的对边分别是，已知，，，则等于( )‎ A. 2 B. 3 C. 4 D. 5‎ ‎【答案】B ‎【解析】由余弦定理得，即，所以，应选答案B。‎ ‎8．袋中有形状、大小都相同的4个球，其中2个红球、2个白球.从中随机一次摸出2个球，则这2个球中至少有1个白球的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】袋中有形状、大小都相同的4个球，其中2个红球，2个白球。‎ 从中随机一次摸出2个球，‎ 基本事件总数，‎ 这2个球中至少有1个白球的对立事件是这2个球中都是红球，‎ ‎∴这2个球中至少有1个白球的概率.‎ 故选：D.‎ ‎9．执行如图的程序框图，则输出的值为（ ）‎ A. B. C. 2 D. ‎ ‎【答案】A ‎【解析】程序执行如下：‎ 首先初始化数值： ，‎ 进入第一次循环： ，‎ 此时不满足，执行；‎ 进入第二次循环： ，‎ 此时不满足，执行；‎ 进入第三次循环： ，‎ 此时不满足，执行；‎ 进入第四次循环： ，‎ 此时不满足，执行；‎ 进入第五次循环后S的数值按照： 四个数循环依次出现，‎ 则当时，程序跳出循环，输出.‎ 本题选择A选项.‎ ‎10．某市重点中学奥数培训班共有14人，分为两个小组，在一次阶段考试中两个小组成绩的茎叶图如图所示，其中甲组学生成绩的平均数是88，乙组学生成绩的中位数是89，则的值是（ ）‎ A. 10 B. 11 C. 12 D. 13‎ ‎【答案】C ‎【解析】试题分析：：∵甲组学生成绩的平均数是88，‎ ‎∴由茎叶图可知78+86+84+88+95+90+m+92=88×7，∴m=3‎ 又乙组学生成绩的中位数是89，∴n=9，‎ ‎∴m+n=12‎ ‎【考点】茎叶图 ‎11．设实数满足约束条件，则的最小值为( )‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】绘制目标函数所表示的可行域如图所示：‎ 结合目标函数的几何意义可得，目标函数在点处取得最小值.‎ 本题选择A选项.‎ 点睛：(1)求目标函数最值的一般步骤为：一画、二移、三求．其关键是准确作出可行域，理解目标函数的意义．‎ ‎(2)在约束条件是线性的情况下，线性目标函数只有在可行域的顶点或者边界上取得最值．在解答选择题或者填空题时可以根据可行域的顶点直接进行检验．‎ ‎12．已知各项均为正数的等比数列满足，若存在两项使得 ‎，则的最大值为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】设各项均为正数的等比数列{an}的公比为q>0,∵a10+a9=6a8,∴a8(q2+q)=6a8，解得q=2.‎ ‎∵存在两项am,an使得,∴，化为：m+n=6.‎ 则，‎ 令.‎ 则.‎ ‎∴最大值为.‎ 本题选择D选项.‎ 二、填空题 ‎13．在1,2,3,6这组数据中随机取出三个数，则数字3是这三个不同数字的中位数的概率是__________．‎ ‎【答案】‎ ‎【解析】在1，2，3，6这组数据中随机取出三个数，基本事件总数，‎ 数字3是这三个不同数字的中位数包含的基本事件有：136，236，有2个基本事件，‎ ‎∴数字3是这三个不同数字的中位数的概率是.‎ 点睛：有关古典概型的概率问题，关键是正确求出基本事件总数和所求事件包含的基本事件数．‎ ‎(1)基本事件总数较少时，用列举法把所有基本事件一一列出时，要做到不重复、不遗漏，可借助“树状图”列举．(2)注意区分排列与组合，以及计数原理的正确使用.‎ ‎14．若样本，的平均数为10，方差为2，则对于样本，其平均数和方差的和为____________．‎ ‎【答案】13‎ ‎【解析】由均值、方差的性质结合题意可知：‎ 样本的平均数为11，方差为2，‎ 则平均数和方差的和为11+2=13.‎ ‎15．圆上的点到直线的距离的最小值为__________．‎ ‎【答案】2‎ ‎【解析】圆的圆心C(1,−2)，半径r=1，‎ 圆心C(1,−2)到直线直线3x−4y+4=0的距离：‎ ‎，‎ ‎∴圆上的点到直线3x−4y+4=0的距离的最小值为：d−r=3−1=2.‎ 故答案为：2.‎ ‎16．某单位为了了解用电量y（度）与气温x（℃）之间的关系，随机统计了某4天的用电量与当天气温（如表），并求得线性回归方程为=－2x+60．不小心丢失表中数据c，d，那么由现有数据知2c+d=______．‎ x c ‎13‎ ‎10‎ ‎－1‎ y ‎24‎ ‎34‎ ‎38‎ d ‎【答案】100‎ ‎【解析】‎ 点睛：函数关系是一种确定的关系，相关关系是一种非确定的关系.事实上，函数关系是两个非随机变量的关系，而相关关系是非随机变量与随机变量的关系.如果线性相关，则直接根据用公式求，写出回归方程，回归直线方程恒过点.‎ 三、解答题 ‎17．东莞市某高级中学在今年4月份安装了一批空调，关于这批空调的使用年限（单位：年， ）和所支出的维护费用（单位：万元）厂家提供的统计资料如下：‎ ‎（1）请根据以上数据，用最小二乘法原理求出维护费用关于的线性回归方程；‎ ‎（2）若规定当维护费用超过13.1万元时，该批空调必须报废，试根据（1）的结论求该批空调使用年限的最大值.‎ 参考公式：最小二乘估计线性回归方程中系数计算公式：‎ ‎， ‎ ‎【答案】（1）；（2）该批空调使用年限的最大值为11年。‎ ‎【解析】试题分析：（1）先求两组数据的平均数，再代入相关系数公式求出，进而确定，求出回归方程；（2）依据题设建立不等式，解出，求出空调使用年限的最大值为11年：‎ 解：（1）因为， ，所以 ‎ ‎ 故线性回归方程为. ‎ ‎（2）当维护费用超过13.1万元时，即 从第12年开始这批空调必须报废，该批空调使用年限的最大值为11年. …………11分 答：该批空调使用年限的最大值为11年. ‎ ‎18．已知数列的首项，前项和为．‎ ‎（1）求数列的通项公式； （2）设，求数列的前项和．‎ ‎【答案】(1) （2） ‎ ‎【解析】试题分析：‎ ‎(1)由数列的递推公式可得数列是首项为1,，公比为3的等比数列，则其通项公式为；‎ ‎(2)结合(1)中求得的通项公式可得： ，分组求和可得数列的前n项和为 .‎ 试题解析：‎ ‎(1)由题意得 两式相减得，‎ 所以当时，是以为公比的等比数列.因为 所以，，对任意正整数成立，是首项为，公比为的等比数列，所以得.‎ ‎（2）， ‎ 所以， ‎ ‎ ‎ ‎19．国庆期间，高速公路堵车现象经常发生.某调查公司为了了解车速，在临川收费站从7座以下小型汽车中按进收费站的先后顺序，每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查，将他们在某段高速公路的车速）分成六段后，得到如图的频率分布直方图.‎ ‎（1）求这40辆小型汽车车速的众数和中位数的估计值；‎ ‎（2）若从这40辆车速在的小型汽车中任意抽取2辆，求抽出的2辆车车速都在的概率．‎ ‎【答案】(1) , (2) ‎ ‎【解析】试题分析：‎ ‎(1)利用频率分布直方图可估计众数为77.5，使得中位数处将频率分布直方图分割为面积相等的两部分，据此列方程可得中位数为77.5；‎ ‎(2)利用古典概型公式可知事件的概率空间共有15种不同的结果，其中满足题意的结果有6种，则满足题意的概率值为.‎ 试题解析：‎ ‎(1)众数的估计值为最高的矩形的中点，即众数的估计值为 由题图可知，中位数应该在之间，设为，‎ 则，解得： ‎ 即中位数的估计值为 ‎ ‎(2)这辆车中，车速在 的共有 (辆)，‎ 其中车速在 的有 (辆)，记为 车速在 的有 (辆)，记为从车速在 的这辆汽车中任意抽取辆的可能结果有种不同的结果，‎ 其中抽出的辆车车速都在 的结果有种 因为抽到每种结果都是等可能的，所以从这辆车速在的汽车中任意抽取辆，‎ 抽出的辆车车速都在 的概率为 点睛：利用频率分布直方图求众数、中位数和平均数时，应注意三点：①最高的小长方形底边中点的横坐标即是众数；②中位数左边和右边的小长方形的面积和是相等的；③平均数是频率分布直方图的“重心”，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.‎ ‎20．如图，在底面是矩形的四棱锥P‒ABCD中，PA⊥平面ABCD，PA = AB = 2，BC = 4， E是PD的中点，‎ ‎（1）求证： 平面EAC； ‎ ‎（2）求证：平面PDC⊥平面PAD； ‎ ‎（3）求多面体的体积．‎ ‎【答案】（1）见解析（2）见解析（3）4‎ ‎【解析】试题分析：‎ ‎(1)做出辅助线，由结合线面平行的判断定理即可证得平面EAC；‎ ‎(2)由题意可证得CD⊥平面PAD，结合面面垂直的判断定理即可证得平面PDC⊥平面PAD；‎ ‎(3)将原问题转化为组合体体积之差的问题，分别求解体积值可得多面体的体积是4.‎ 试题解析：‎ ‎（1）连接BD交AC于点G,连接EG，因为E为PD的中点，G为BD的中点，‎ 所以,又因为, ，‎ 所以.‎ ‎（2），，. ‎ ‎　　　 , . 而, 平面 ‎ . . ‎ ‎（3）,因为E为PD的中点， ,‎ 所以点E到平面ADC的距离是,即 ,‎ 所以 ‎ ‎21．随着互联网的发展，移动支付（又称手机支付）越来越普通，某学校兴趣小组为了了解移动支付在大众中的熟知度，对15-65岁的人群随机抽样调查，调查的问题是“你会使用移动支付吗？”其中，回答“会”的共有个人.把这个人按照年龄分成5组：第1组，第2组，第3组，第4组，第5组，然后绘制成如图所示的频率分布直方图.其中，第一组的频数为20.‎ ‎（1）求 和的值，并根据频率分布直方图估计这组数据的众数；‎ ‎（2）从第1，3，4组中用分层抽样的方法抽取6人，求第1，3，4组抽取的人数；‎ ‎（3）在（2）抽取的6人中再随机抽取2人，求所抽取的2人来自同一个组的概率.‎ ‎【答案】（1），，30；（2）第1组2人，第2组3人，第3组1人；（3）.‎ ‎【解析】试题分析：（1）直接利用频率分布直方图，结合累积频率为1，频数=频率×样本容量，可分别求出 和的值，最高点的中点横坐标即为众数； （2）直接利用抽样比即可求第1，2，3组每组各抽取人数． ‎ ‎（3）列出（2）抽取的6人中随机抽取2人是所有情况，求出这2人来自同一个组的数目，即可求解概率．‎ 试题解析：‎ ‎（1）由题意可知，，‎ 由，‎ 解得，‎ 由频率分布直方图可估计这组数据的众数为30；‎ ‎（2）第1，3，4组频率之比为0.020：0.030：0.010=2：3：1‎ 则从第1组抽取的人数为,‎ 从第3组抽取的人数为，‎ 从第4组抽取的人数为；‎ ‎（3）设第1组抽取的2人为，第3组抽取的3人为，第4组抽取的1人为，则从这6人中随机抽取2人有如下种情形：，‎ ‎，共有15个基本事件.‎ 其中符合“抽取的2人来自同一个组”的基本事件有共4个基本事件，‎ 所以抽取的2人来自同一个组的概率.‎ 点睛：有关古典概型的概率问题，关键是正确求出基本事件总数和所求事件包含的基本事件数．‎ ‎(1)基本事件总数较少时，用列举法把所有基本事件一一列出时，要做到不重复、不遗漏，可借助“树状图”列举．(2)注意区分排列与组合，以及计数原理的正确使用.‎ ‎22．已知圆和圆．‎ ‎（1）判断圆和圆的位置关系；‎ ‎（2）过圆的圆心作圆的切线，求切线的方程；‎ ‎（3）过圆的圆心作动直线交圆于A，B两点．试问：在以AB为直径的所有圆中，是否存在这样的圆，使得圆经过点？若存在，求出圆的方程；若不存在，请说明理由．‎ ‎【答案】（1）外离；‎ ‎（2）或；‎ ‎（3）存在圆：或，使得圆经过点 。‎ ‎【解析】试题分析：（1）求出两圆的圆心距，在比较其与 的大小关系，从而确定两圆的位置关系；（2）由点 ‎ 斜式设出切线方程，然后用点线距离公式建立关于的方程；（2）斜率不存在时，易知圆也是满足题意的圆；斜率存在时，假设存在以为直径的圆经过点，则，所以，则可得，再把直线方程与圆的方程联立可求，，代入上式可得关于的方程。‎ ‎(1)因为圆的圆心，半径，圆的圆心，半径，‎ 所以圆和圆的圆心距，‎ 所以圆与圆外离. 3分 ‎（2）设切线的方程为：，即，‎ 所以到的距离，解得.‎ 所以切线的方程为或. ....7分 ‎ (3)ⅰ）当直线的斜率不存在时，直线经过圆的圆心，此时直线与圆的交点为，，即为圆的直径，而点在圆上，即圆也是满足题意的圆．.......8分 ⅱ）当直线的斜率存在时，设直线，由，‎ 消去整理，得，‎ 由△，得或．‎ 设，则有 ① 9分 由①得， ②‎ ‎， ③‎ 若存在以为直径的圆经过点，则，所以，‎ 因此，即， 10分 则，所以，，满足题意．‎ 此时以为直径的圆的方程为，‎ 即，亦即． 12分 综上，在以AB为直径的所有圆中，存在圆：或 ‎，使得圆经过点． 14分 ‎【考点】（1）两圆位置关系的判断；（2）圆的切线方程的求法；（3）斜率引起的分类讨论；（2）直线与圆的位置关系。 ‎