高一物理专题复习三：曲线运动与万有引力人教实验版

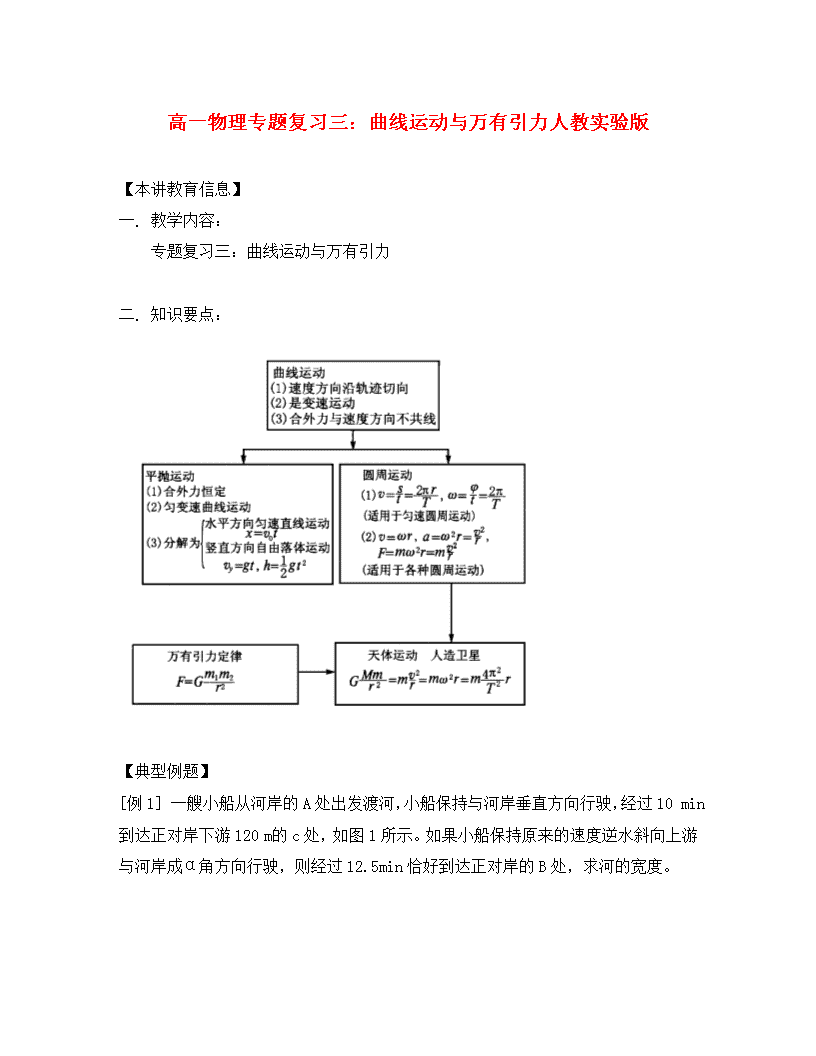
高一物理专题复习三：曲线运动与万有引力人教实验版

高一物理专题复习三：曲线运动与万有引力人教实验版 ‎ ‎【本讲教育信息】‎ 一. 教学内容：‎ 专题复习三：曲线运动与万有引力 二. 知识要点：‎ ‎【典型例题】‎ ‎[例1] 一艘小船从河岸的A处出发渡河，小船保持与河岸垂直方向行驶，经过10 min到达正对岸下游‎120 m的c处，如图1所示。如果小船保持原来的速度逆水斜向上游与河岸成α角方向行驶，则经过12.5min恰好到达正对岸的B处，求河的宽度。‎ 图1‎ 解析：解决这类问题的关键是画好速度合成的示意图，画图时首先要明确哪是合运动哪是分运动。对本题来讲，AC和AB是两个不同运动过程中船相对于岸的实际运动方向，那么AB和AC就是速度合成平行四边形的对角线。一旦画好平行四边形，剩下的工作就是根据运动的等时性以及三角形的边角关系列方程求解了。‎ 设何宽为d，河水流速为v水，船速为v船，船两次运动的速度合成如图2和3所示。‎ ‎ ‎ 图2 图3‎ 第一次渡河与第二次渡河在垂直岸的方向上位移相等，则v船t1=v船sinαt2 ①‎ 第一次渡河沿水流方向上位移为BC，则 BC=v水t1 ②‎ 由图3可得船的合速度：v＝v水tanα，所以河的宽度为d=vt 2＝v水tanαt2 ③‎ 由①式得sinα＝0.8，故tanα＝‎ 由②式得 v水＝12 m／min 代入③式可得河宽d=12××12.5 rn＝200 m ‎[例2] A、B两个小球由柔软的细线相连，线长l=‎6m；将A、B球先后以相同的初速度v0=‎4.5m/s，从同一点水平抛出（先A、后B）相隔时间△t =0.8s。‎ ‎（1）A球抛出后经多少时间，细线刚好被拉直？‎ ‎（2）细线刚被拉直时，A、B球的水平位移（相对于抛出点）各多大？（取g=10m/s2）‎ 解答：（1）A、B两球以相同的初速度v0，从同一点水平抛出，可以肯定它们沿同一轨道运动。‎ 作细线刚被拉直时刻A、B球位置示意图 根据题意可知：‎ 设A球运动时间为t，则B球运动时间为t－0.8，由于A、B球在竖直方向上均作自由落体运动，所以有。‎ 由此解得t =1s。‎ ‎（2）细线刚被拉直时，‎ A、B球的水平位移分别为 ‎[例3] 假设有两个天体，质量分别为m1和m2，它们相距r；其他天体离它们很远，可以认为这两个天体除相互吸引作用外，不受其他外力作用，这两个天体之所以能保持距离r不变，完全是由于它们绕着共同“中心”（质心）做匀速圆周运动，它们之间的万有引力作为做圆周运动的向心力，“中心”O位于两个天体的连线上，与两个天体的距离分别为r1和r2。‎ ‎（1）r1、r2各多大？‎ ‎（2）两天体绕质心O转动的角速度、线速度、周期各多大？‎ 解答：根据题意作图。‎ 对这两个天体而言，它们的运动方程分别为 ①‎ ‎ ②‎ 以及 ③‎ 由以上三式解得 将r1和r2的表达式分别代①和②式，‎ 可得 ‎[例4] 宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球，经过时间t，小球落到星球表面。测得抛出点与落地点之间的距离为L，若抛出时的初速度增大到2倍，则抛出点与落地点之间的距离为L，已知两落地点在同一水平面上，该星球的半径为R，万有引力常量为G，求该星球的质量M。‎ 解析：设抛出点的高度为h，第一次水平位移为x，则有 x2十h2＝L2 ①‎ 同理对于第二次平抛过程有：（2x）2十h2＝（）2 ②‎ 由①②解得h＝　　　　　　　　　　　　　　　　　‎ 设该行星上重力加速度为g，由平抛运动规律得 h＝　③‎ 由万有引力与牛顿第二定律得mg＝G　 ④‎ 联立以上各式可解得M＝。‎ 说明：（1）审题时一定要注意，抛出点与落地点之间的距离不是水平位移。‎ ‎　　　（2）求解本题的关键是找出该星球上的重力加速度g ‎【模拟试题】‎ ‎1. 如图所示；小车内有一光滑斜面，当小车在水平轨道上做匀变速直线运动时，小物块A恰好能与斜面保持相对静止，在小车运动过程中的某时刻（此时小车速度不为0），使小车迅速停止，则在小车停止的过程中，小物块A可能（ ）‎ A. 沿斜面滑下 B. 沿斜面滑上去　‎ C. 仍与斜面保持相对静止 D. 离开斜面作曲线运动 ‎2. 一人骑自行车向东行驶，当车速为‎4m／s时，他感到风从正南方向吹来，当车速增加到‎7m／s时。他感到风从东南方向（东偏南45º）吹来，则风对地的速度大小为（ ）‎ A. ‎7m/s B. ‎6m／s C. ‎5m／s D. ‎4 m／s ‎3. 如图所示，两轮用皮带传动，皮带不打滑，图中有A、B、C三点，这三点所在处半径rA>rB＝rC，则这三点的向心加速度aA、aB、aC的关系是（ ）‎ A. aA=aB＝aC 　 B. aA＞aB＞aC C. aC

查看更多