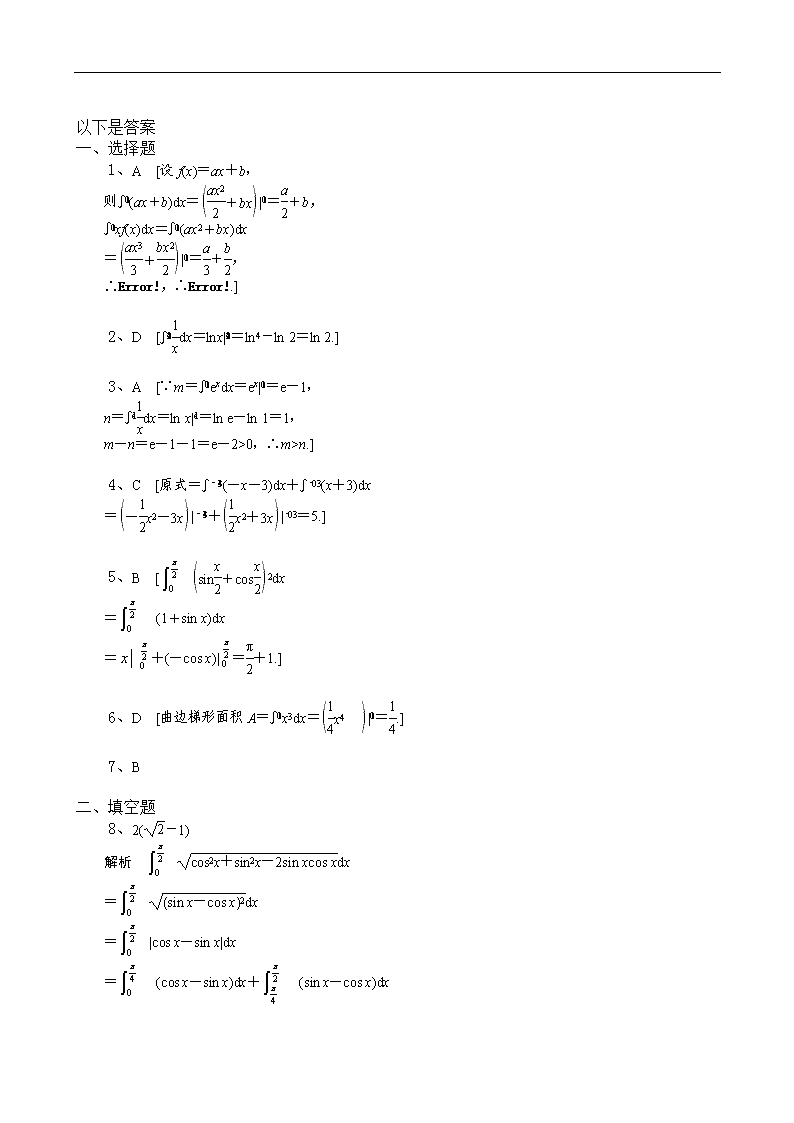高考数学专题复习:微积分基本定理
1.6微积分基本定理
一、选择题
1、f(x)是一次函数,且ʃf(x)dx=5,ʃxf(x)dx=,那么f(x)的解析式是( )
A.4x+3 B.3x+4
C.-4x+2 D.-3x+4
2、ʃdx等于( )
A.-2ln 2 B.2ln 2
C.-ln 2 D.ln 2
3、若m=ʃexdx,n=ʃdx,则m与n的大小关系是( )
A.m>n B.m
0,∴m>n.]
4、C [原式=ʃ(-x-3)dx+ʃ(x+3)dx
=|+|=5.]
5、B [2dx
= (1+sin x)dx
=+(-cos x)|=+1.]
6、D [曲边梯形面积A=ʃx3dx=|=.]
7、B
二、填空题
8、2(-1)
解析 dx
=dx
=|cos x-sin x|dx
= (cos x-sin x)dx+ (sin x-cos x)dx
=(sin x+cos x)|-(cos x+sin x)|=2(-1).
9、ln 2
解析 ∵′=,
∴ʃdx=ln(1+x2)|=ln 2.
10、1
解析 ∵ʃ(2xk+1)dx=ʃ2xkdx+ʃdx
=2ʃxkdx+x|=|+1
=+1=2,∴=1,
即k=1.
三、解答题
11、解 ∵f(x)=x3+ax为奇函数,
∴ʃ(x3+ax)dx=0,
∴ʃ(x3+ax+3a-b)dx
=ʃ(x3+ax)dx+ʃ(3a-b)dx
=0+(3a-b)[1-(-1)]=6a-2b.
∴6a-2b=2a+6,
即2a-b=3.①
又f(t)=
=++(3a-b)t为偶函数,
∴3a-b=0.②
由①②得a=-3,b=-9.
12、解 f(x)dx= (asin x+bcos x)dx
=(bsin x-acos x)|
=b+a=4.
f(x)dx=(bsin x-acos x)|
=b-a+a=,
解得a=3,b=1.
所以f(x)=3sin x+cos x=sin(x+φ),(其中tan φ=).
故f(x)的最大值为,最小值为-.
13、解 (1)∵f(x)=sin5x+x13,x∈[-5,5]是奇函数,
∴由定积分的几何意义知
ʃ(sin5x+x13)dx=-ʃ(sin5x+x13)dx,
∴ʃ(sin5x+x13)dx
=ʃ(sin5x+x13)dx+ʃ(sin5x+x13)dx=0.
(2)∵f(x)=cos2x+8,x∈是偶函数,
∴ (cos2x+8)dx=2 (cos2x+8)dx
=2cos2xdx+16dx
= (1+cos 2x)dx+16x|
=|+16x|=π.