- 2021-04-14 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习人教A版算法与程序框图教案
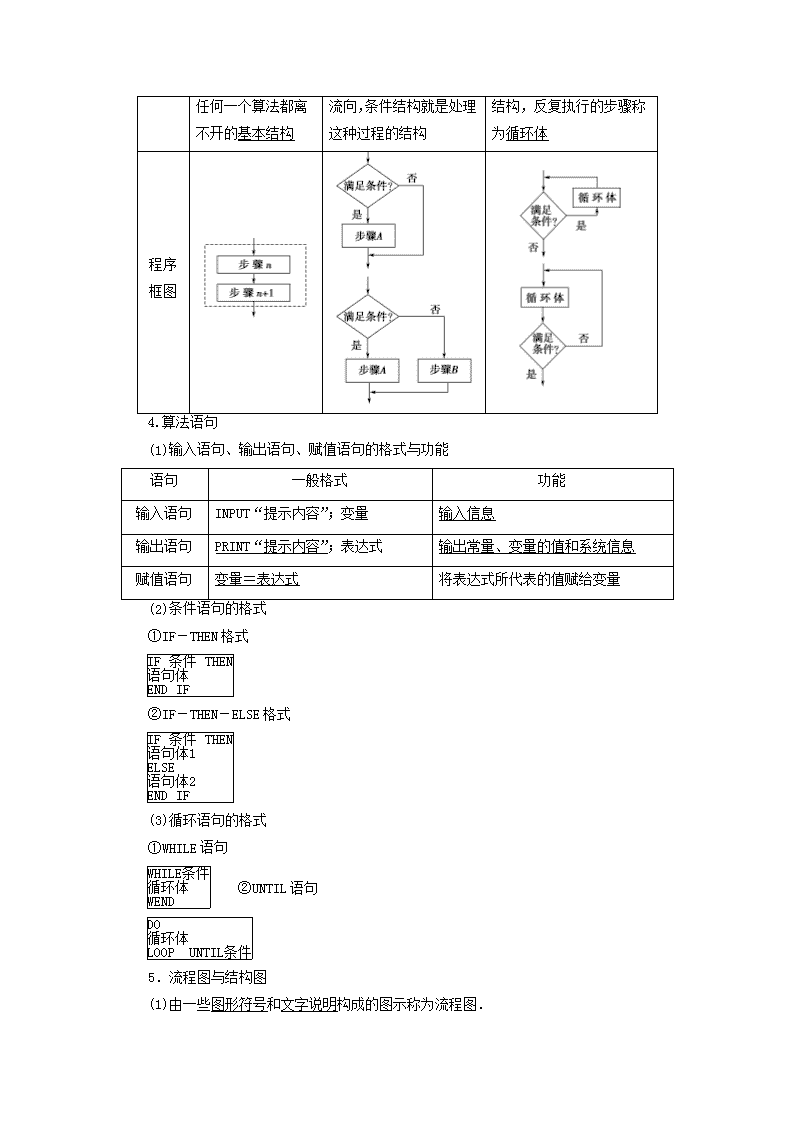
第九章 算法初步、统计与统计案例 [深研高考·备考导航] 为教师授课、学生学习提供丰富备考资源 [五年考情] 考点 2016 年 2015 年 2014 年 2013 年 2012 年 算法、程序 框图、基本 算法语句 全国卷 Ⅰ·T10 全国卷 Ⅱ·T9 全国卷 Ⅲ·T8 全国卷 Ⅰ·T9 全国卷 Ⅱ·T8 全国卷 Ⅰ·T9 全国卷 Ⅱ·T8 全国卷Ⅰ·T7 全国卷Ⅱ·T7 全国 卷·T6 随机抽样 全国卷Ⅰ·T3 用样本估计 总体 全国卷 Ⅰ·T19 全国卷 Ⅱ·T18 全国卷 Ⅲ·T4 全国卷 Ⅱ·T18 全国卷 Ⅰ·T18 全国卷 Ⅱ·T19 全国卷Ⅰ·T18 全国卷Ⅱ·T19 全国 卷·T18 变量间的相 关关系与统 计案例 全国卷 Ⅲ·T18 全国卷 Ⅰ·T19 全国 卷·T3 [重点关注] 综合近 5 年全国卷高考试题,我们发现高考命题在本章呈现以下规律: 1.从考查题型看:一般有 1 个客观题,1 个解答题;从考查分值看,在 17 分左右.基 础题主要考查对基础知识和基本方法的掌握,中档题主要考查数据的处理能力和综合应用能 力. 2.从考查知识点看:主要考查程序框图、简单随机抽样、用样本估计总体、变量间的 相关关系与统计案例.突出对数形结合思想、转化与化归思想、分类讨论思想以及探究、创 新能力的考查. 3.从命题思路上看: (1)求程序框图的执行结果. (2)确定条件结构中的条件与循环结构中的控制变量,完善程序框图. (3)随机抽样中的系统抽样与分层抽样. (4)样本的平均数、频率、中位数、众数、方差;频率分布直方图、茎叶图;变量间的 相关关系中的线性回归分析及独立性检验的基本思想及其初步应用. [导学心语] 1.深刻理解并掌握以下概念 算法中三种结构的功能,抽样方法的操作步骤,数字特征的含义及计算,频率分布直方 图和茎叶图的画法,回归分析中线性回归方程的含义及求法和独立性检验的基本思想. 2.突出重点、控制难度 本章命题背景新颖、重点内容突出:如程序框图的执行结果与条件判断、统计图表与样 本数字特征等,但题目难度不超过中等程度,复习时注意新材料、新背景的题目,重基础, 控制好难度. 3.注重交汇,突出统计思想 强化统计思想方法的应用,注重知识的交汇渗透,如程序框图与数列、统计与函数、统 计图表与概率.复习时善于把握命题新动向,抓住命题的增长点,强化规范性训练,力争不 失分、得满分. 第一节 算法与程序框图 ———————————————————————————————— [考纲传真] 1.了解算法的含义,了解算法的思想.2.理解程序框图的三种基本逻辑结 构:顺序、条件分支、循环.3.了解几种基本算法语句——输入语句、输出语句、赋值语句、 条件语句、循环语句的含义.4.了解流程图、结构图及其在实际中的应用. 1.算法 (1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤. (2)应用:算法通常可以编成计算机程序,让计算机执行并解决问题. 2.程序框图 定义:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形. 3.三种基本逻辑结构 名称 内容 顺序结构 条件结构 循环结构 定义 由若干个依次执行 的步骤组成,这是 任何一个算法都离 算法的流程根据给定的 条件是否成立有不同的 流向,条件结构就是处理 从某处开始,按照一定的 条件反复执行某些步骤的 结构,反复执行的步骤称 不开的基本结构 这种过程的结构 为循环体 程序 框图 4.算法语句 (1)输入语句、输出语句、赋值语句的格式与功能 语句 一般格式 功能 输入语句 INPUT“提示内容”;变量 输入信息 输出语句 PRINT“提示内容”;表达式 输出常量、变量的值和系统信息 赋值语句 变量=表达式 将表达式所代表的值赋给变量 (2)条件语句的格式 ①IF-THEN 格式 IF 条件 THEN 语句体 END IF ②IF-THEN-ELSE 格式 IF 条件 THEN 语句体 1 ELSE 语句体 2 END IF (3)循环语句的格式 ①WHILE 语句 WHILE 条件 循环体 WEND ②UNTIL 语句 DO 循环体 LOOP UNTIL 条件 5.流程图与结构图 (1)由一些图形符号和文字说明构成的图示称为流程图. (2)描述系统结构的图示称为结构图,一般由构成系统的若干要素和表达各要素之间关 系的连线(或方向箭头)构成. 1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)程序框图中的图形符号可以由个人来确定.( ) (2)一个程序框图一定包含顺序结构,但不一定包含条件结构和循环结构.( ) (3)“当型”循环与“直到型”循环退出循环的条件不同.( ) (4)在算法语句中,X=X+1 是错误的.( ) [答案] (1)× (2)√ (3)√ (4)× 2.(教材改编)根据给出的程序框图,计算 f(-1)+f(2)=( ) 图 911 A.0 B.1 C.2 D.4 A [f(-1)=4×(-1)=-4,f(2)=22=4, ∴f(-1)+f(2)=-4+4=0.] 3.(2017·贵阳调研)执行如图 912 所示的程序框图,输出 S 的值为( ) 图 912 A.- 3 2 B. 3 2 C.-1 2 D.1 2 D [按照程序框图依次循环运算,当 k=5 时,停止循环,当 k=5 时,S=sin5π 6 =1 2 .] 4.(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,如图 913 是实现该算 法的程序框图.执行该程序框图,若输入的 x=2,n=2,依次输入的 a 为 2,2,5,则输出的 s=( ) 图 913 A.7 B.12 C.17 D.34 C [输入 x=2,n=2.第一次,a=2,s=2,k=1,不满足 k>n; 第二次,a=2,s=2×2+2=6,k=2,不满足 k>n; 第三次,a=5,s=6×2+5=17,k=3,满足 k>n,输出 s=17.] 5.执行下边的程序框图,若输入的 x 的值为 1,则输出的 y 的值是________. 图 914 13 [当 x=1 时,1<2,则 x=1+1=2,当 x=2 时,不满足 x<2,则 y=3×22+1= 13.] 程序框图的基本结构 (1)(2017·福州调研)阅读如图 915 所示的程序框图,运行相应的程序,若 输入 x 的值为 1,则输出 y 的值为( ) 图 915 A.2 B.7 C.8 D.128 (2)(2016·北京高考)执行如图 916 所示的程序框图,输出的 s 值为( ) 图 916 A.8 B.9 C.27 D.36 (1)C (2)B [(1)由程序框图知,y= 2x,x≥2, 9-x,x<2. ∵输入 x 的值为 1,比 2 小, ∴执行的程序要实现的功能为 9-1=8,故输出 y 的值为 8. (2)k=0,s=0,满足 k≤2;s=0,k=1,满足 k≤2;s=1,k=2,满足 k≤2; s=1+23=9,k=3,不满足 k≤2,输出 s=9.] [规律方法] 1.对条件结构,无论判断框中的条件是否成立,都只能执行两个分支中的 一个,不能同时执行两个分支. 2.利用循环结构表示算法,第一要确定是利用当型循环还是直到型循环结构;第二要 准确表示累计变量;第三要注意从哪一步开始循环.弄清进入或终止的循环条件、循环次数 是做题的关键. [变式训练 1] (1)根据如图 917 所示程序框图,当输入 x 为 6 时,输出的 y=( ) 图 917 A.1 B.2 C.5 D.10 (2)我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十 尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描 述,如图 918 所示,则输出结果 n=( ) 图 918 A.4 B.5 C.2 D.3 (1)D (2)A [(1)当 x=6 时,x=6-3=3,此时 x=3≥0; 当 x=3 时,x=3-3=0,此时 x=0≥0; 当 x=0 时,x=0-3=-3,此时 x=-3<0, 则 y=(-3)2+1=10. (2)该程序框图运行 4 次,第 1 次循环,a=1,A=1,S=2,n=1;第 2 次循环,a=1 2 , A=2,S=9 2 ,n=2;第 3 次循环,a=1 4 ,A=4,S=35 4 ,n=3;第 4 次循环,a=1 8 ,A=8,S =135 8 ,n=4,此时循环结束,则输出的 n=4,故选 A.] 程序框图的识别与完善 ☞角度 1 求程序框图执行的结果 (2016·全国卷Ⅰ)执行下面的程序框图,如果输入的 x=0,y=1,n=1,则 输出 x,y 的值满足( ) 图 919 A.y=2x B.y=3x C.y=4x D.y=5x C [输入 x=0,y=1,n=1,运行第一次,x=0,y=1,不满足 x2+y2≥36;运行第二 次,x=1 2 ,y=2,不满足 x2+y2≥36;运行第三次,x=3 2 ,y=6,满足 x2+y2≥36,输出 x =3 2 ,y=6.由于点 3 2 ,6 在直线 y=4x 上,故选 C.] ☞角度 2 完善程序框图 执行如图 9110 所示的程序框图,若输出 k 的值为 8,则判断框内可填入的 条件是( ) 【导学号:31222354】 图 9110 A . s≤ 3 4 ? B . s≤ 5 6 ? C . s≤ 11 12 ? D.s≤25 24 ? C [执行第 1 次循环,则 k=2,s=1 2 ,满足条件. 执行第 2 次循环,则 k=4,s=1 2 +1 4 =3 4 ,满足条件. 执行第 3 次循环,则 k=6,s=3 4 +1 6 =11 12 ,满足条件.执行第 4 次循环,k=8,s=11 12 + 1 8 =25 24 ,不满足条件,输出 k=8, 因此条件判断框应填 s≤11 12 ?.] [规律方法] 1.(1)第 1 题的关键在于理解程序框图的功能;(2)第 2 题要明确何时进入 或退出循环体,以及累加变量的变化. 2.解答此类题目:(1)要明确程序框图的顺序结构、条件结构和循环结构;(2)理解程 序框图的功能;(3)要按框图中的条件运行程序,按照题目的要求完成解答. 基本算法语句 根据下面算法语句,当输入 x 为 60 时,输出 y 的值为( ) INPUT x IF x<=50 THEN y=0.5x ELSE y=25+0.6 x-50 END IF PRINT y A.25 B.30 C.31 D.61 C [由题知,算法语句是一个分段函数 y=f(x)= 0.5x,x≤50, 25+0.6 x-50 ,x>50, ∴y=f(60)=25+0.6×(60-50)=31.] [规律方法] 1.本题主要考查条件语句,输入、输出语句与赋值语句,要注意赋值语句 一般格式中的“=”不同于等式中的“=”,其实质是计算“=”右边表达式的值,并将该 值赋给“=”左边的变量. 2.解决此类问题关键要理解各语句的含义,以及基本算法语句与算法结构的对应关系. [变式训练 2] 按照如下程序运行,则输出 k 的值是________. x=3 k=0 DO x=2x+1 k=k+1 LOOP UNTIL x>16 PRINT k END 3 [第一次循环,x=7,k=1; 第二次循环,x=15,k=2; 第三次循环,x=31,k=3. 终止循环,输出 k 的值是 3.] [思想与方法] 1.每个算法结构都含有顺序结构,循环结构中必定包含一个条件结构,用于确定何时 终止循环体,循环结构和条件结构都含有顺序结构. 2.利用循环结构表示算法,要明确是利用当型循环结构,还是直到型循环结构.要注 意:(1)选择好累计变量;(2)弄清在哪一步开始循环,满足什么条件不再执行循环体. [易错与防范] 1.赋值号左边只能是变量(不是表达式),在一个赋值语句中只能给一个变量赋值. 2.注意条件结构与循环结构的联系: 循环结构有重复性,条件结构具有选择性没有重复性,并且循环结构中必定包含一个条 件结构,用于确定何时终止循环体. 3.当型循环与直到型循环的区别: 直到型循环是“先循环,后判断,条件满足时终止循环”;而当型循环则是“先判断, 后循环,条件满足时执行循环”.两者的判断框内的条件表述在解决同一问题时是不同的, 它们恰好相反. 课时分层训练(五十四) 算法与程序框图 A 组 基础达标 (建议用时:30 分钟) 一、选择题 1.执行如图 9111 所示的程序框图,若输入的实数 x=4,则输出结果为 ( ) 图 9111 A.4 B.3 C.2 D.1 4 C [依题意,输出的 y=log24=2.] 2.(2017·天津河西区调研)阅读程序框图 9112,运行相应的程序,则输出 S 的值为 ( ) 图 9112 A.-10 B.6 C.14 D.18 B [程序框图为直到型循环结构,初始值 S=20,i=1. 执行一次循环,i=2,S=20-2=18; 执行两次循环,i=2×2=4,S=18-4=14; 执行三次循环,i=2×4=8,S=14-8=6 满足 i>5,终止循环,输出 S=6.] 3.(2016·四川高考)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他 在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图 9113 所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入 n,x 的值 分别为 3,2,则输出 v 的值为( ) 图 9113 A.35 B.20 C.18 D.9 C [由程序框图知,初始值:n=3,x=2,v=1,i=2, 第一次:v=4,i=1; 第二次:v=9,i=0; 第三次:v=18,i=-1. i=-1<0,结束循环,输出 v=18,故选 C.] 4.(2016·郑州模拟)随机抽取某产品 n 件,测得其长度分别是 a1,a2,…,an,如图 9114 所示的程序框图输出样本的平均值为 s,则在处理框①中应填入的式子是( ) 图 9114 A.s=s+ai i B.s=is+ai i+1 C.s=s+ai D.s= i-1 s+ai i D [设 a1+a2+…+ai=Si,则在第 i-1 次时 Si-1=(i-1)s,在第 i 次时 Si=Si-1+ai, ∴s=Si i =Si-1+ai i = i-1 s+ai i ,故选 D.] 5.(2016·天津高考)阅读下边的程序框图,运行相应的程序,则输出 S 的值为( ) 图 9115 A.2 B.4 C.6 D.8 B [S=4 不满足 S≥6,S=2S=2×4=8,n=1+1=2; n=2 不满足 n>3,S=8 满足 S≥6,则 S=8-6=2,n=2+1=3; n=3 不满足 n>3,S=2 不满足 S≥6,则 S=2S=2×2=4,n=3+1=4; n=4 满足 n>3,输出 S=4.故选 B.] 6.(2015·全国卷Ⅱ)下边程序框图的算法思路源于我国古代数学名著《九章算术》中 的“更相减损术”.执行该程序框图,若输入的 a,b 分别为 14,18,则输出的 a=( ) 图 9116 A.0 B.2 C.4 D.14 B [a=14,b=18. 第一次循环:14≠18 且 14<18,b=18-14=4; 第二次循环:14≠4 且 14>4,a=14-4=10; 第三次循环:10≠4 且 10>4,a=10-4=6; 第四次循环:6≠4 且 6>4,a=6-4=2; 第五次循环:2≠4 且 2<4,b=4-2=2; 第六次循环:a=b=2,跳出循环,输出 a=2,故选 B.] 二、填空题 7.(2017·江南名校联考)某程序框图如图 9117 所示,判断框内为“k≥n?”,n 为 正整数,若输出的 S=26,则判断框内的 n=________. 【导学号:31222355】 图 9117 4 [依题意,执行题中的程序框图,进行第一次循环时,k=1+1=2,S=2×1+2=4; 进行第二次循环时,k=2+1=3,S=2×4+3=11;进行第三次循环时,k=3+1=4,S= 2×11+4=26. 因此当输出的 S=26 时,判断框内的条件 n=4.] 8.执行如图 9118 所示的程序框图(算法流程图),输出的 n 为________. 【导学号:31222356】 图 9118 4 [执行第一次判断:|a-1.414|=0.414>0.005,a=3 2 ,n=2; 执行第二次判断:|a-1.414|=0.086>0.005,a=7 5 ,n=3; 执行第三次判断:|a-1.414|=0.014>0.005,a=17 12 ,n=4; 执行第四次判断:|a-1.414|<0.005,输出 n=4.] 9.执行下边的程序,输出的结果是________. 【导学号:31222357】 S=1 i=3 WHILE S<=200 S=S×i i=i+2 WEND PRINT i END 11 [根据循环结构可得:第一次,S=1×3=3,i=3+2=5,由于 3≤200,则循环; 第二次:S=3×5=15,i=5+2=7,由于 15≤200,则循环; 第三次:S=15×7=105,i=7+2=9,由于 105≤200,则循环; 第四次:S=105×9=945,i=9+2=11,由于 945>200,则循环结束,故此时输出 i =11.] 10.(2017·石家庄质检)执行如图 9119 所示的程序框图,如果输入的 t=50,则输 出的 n=________. 图 9119 6 [第一次运行后 S=2,a=3,n=1; 第二次运行后 S=5,a=5,n=2; 第三次运行后 S=10,a=9,n=3; 第四次运行后 S=19,a=17,n=4; 第五次运行后 S=36,a=33,n=5; 第六次运行后 S=69,a=65,n=6, 此时不满足 S<t,退出循环,输出 n=6.] B 组 能力提升 (建议用时:15 分钟) 1.(2016·全国卷Ⅲ)执行下面的程序框图,如果输入的 a=4,b=6,那么输出的 n= ( ) 图 9120 A.3 B.4 C.5 D.6 B [开始 a=4,b=6,n=0,s=0. 第 1 次循环:a=2,b=4,a=6,s=6,n=1; 第 2 次循环:a=-2,b=6,a=4,s=10,n=2; 第 3 次循环:a=2,b=4,a=6,s=16,n=3; 第 4 次循环:a=-2,b=6,a=4,s=20,n=4. 此时,满足条件 s>16,退出循环,输出 n=4.故选 B.] 2.(2017·长沙一中质检)如图 9121 所示的程序框图,如果输入 n=3,则输出的 S =( ) 图 9121 A.6 7 B.3 7 C.8 9 D.4 9 B [第一次循环:S= 1 1×3 ,i=2; 第二次循环:S= 1 1×3 + 1 3×5 ,i=3; 第三次循环:S= 1 1×3 + 1 3×5 + 1 5×7 ,i=4,满足循环条件,结束循环. 故输出 S= 1 1×3 + 1 3×5 + 1 5×7 =1 2 1-1 3 +1 3 -1 5 +1 5 -1 7 =3 7 ,故选 B.] 3.执行如图 9122 所示的程序框图,若输入的 x 的值为 1,则输出的 n 的值为________. 图 9122 3 [按照程序框图逐一执行. 由 x2-4x+3≤0,解得 1≤x≤3. 当 x=1 时,满足 1≤x≤3,所以 x=1+1=2,n=0+1=1; 当 x=2 时,满足 1≤x≤3,所以 x=2+1=3,n=1+1=2; 当 x=3 时,满足 1≤x≤3,所以 x=3+1=4,n=2+1=3; 当 x=4 时,不满足 1≤x≤3,所以输出 n=3.] 4.关于函数 f(x)= -x,1<x≤4, cos x,-1≤x≤1 的程序框图如图 9123 所示,现输入区间[a, b],则输出的区间是________. 图 9123 [0,1] [由程序框图的第一个判断条件为 f(x)>0,当 f(x)=cos x,x∈[-1,1]时满 足.然后进入第二个判断框,需要解不等式 f′(x)=-sin x≤0,即 0≤x≤1.故输出区间 为[0,1].]查看更多