专题04++函数的零点与方程的根的解题方法-名师揭秘2019年高考数学(文)命题热点全覆盖(教师版)
专题04 函数的零点与方程的根的解题方法
本专题特别注意:
一.命题类型:
1.零点与整数解;
2.二分法;
3.分段函数的零点;
4.零点范围问题;
5.零点个数问题;
6.零点与参数;
7.零点与框图;
8.二次函数零点分布问题;
9.抽象函数零点问题;
10.复合函数零点问题;
11.函数零点与导数;
12.零点有关的创新试题。
二.【学习目标】
1.结合二次函数的图象,了解函数的零点与方程根的联系,判断根的存在性与根的个数.
2.利用函数的零点求解参数的取值范围
【知识要点】
1.函数的零点
(1)函数零点的定义
对于函数y=f(x),我们把使___________的实数x叫做函数y=f(x)的零点.
(2)方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有________.
(3)函数零点的判定
如果函数y=f(x)在区间[a,b]上的图象是_________的一条曲线,并且有____________,那么,函数y=f(x)在区间__________内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
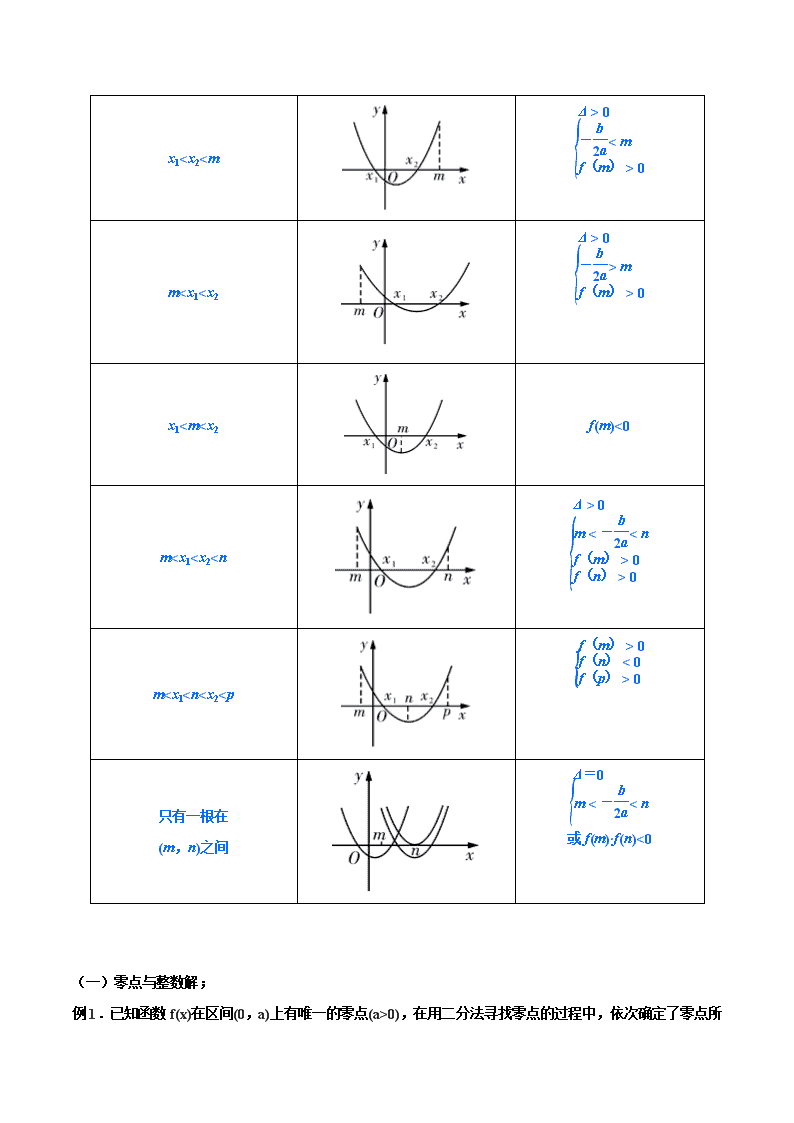
2.二次函数y=f(x)=ax2+bx+c(a>0)零点的分布
根的分布
(m
0),在用二分法寻找零点的过程中,依次确定了零点所在的区间为,,,则下列说法中正确的是( )
A.函数f(x)在区间内一定有零点
B.函数f(x)在区间或内有零点,或零点是
C.函数f(x)在内无零点
D.函数f(x)在区间或内有零点
【答案】B
点睛:本题主要考查二分法的定义,属于基础题.已经知道零点所在区间,根据二分法原理,依次“二分”区间,零点应存在于更小的区间, 而不是更大的区间。这样就可以断定ACD是错误的。故可以得到结论。
练习1.【河北定州2019模拟】设函数,若存在唯一的整数,使得,则的取值范围是( )
A. B. C. D.
【答案】D
【解析】当直线
令,
,函数在上为减函数,在上为增函数,当时,取得极小值为,时,,当时,,若存在唯一的整数,使得,即,只需解得: ,选D.
练习2.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2﹣2x﹣3,求当x≤0时,不等式f(x)≥0整数解的个数为( )
A.4 B.3 C.2 D.1
【答案】A
【解析】由函数为奇函数可知当x≤0时,不等式f(x)≥0整数解的个数与时的个数相同,由奇函数可知,由得,所以整数解为1,2,3,所以满足题意要求的整数点有4个
(二)二分法;
例2.下面关于二分法的叙述中,正确的是 ( )
A.用二分法可求所有函数零点的近似值
B.用二分法求方程的近似解时,可以精确到小数点后的任一位
C.二分法无规律可循,无法在计算机上完成
D.只能用二分法求函数的零点
【答案】B
【解析】用二分法求函数零点的近似值,需要有端点函数值符号相反的区间,故选项A错误;
二分法是一种程序化的运算,故可以在计算机上完成,故选项C错误;
求函数零点的方法还有方程法、函数图象法等,故D错误.故选B.
练习1.已知函数,设,且的零点均在区间内,其中,,,则的最小整数解为( )
A. B. C. D.
【答案】D
【解析】,所以函数在内有零点,且在区间上,,函数递增,故只有唯一零点,左移个单位得到,依题意,函数所有零点都在区间上,所以使得的最小整数为.
考点:函数图象平移与零点.
【思路点晴】本题主要考查函数图象变换和零点与二分法的知识.由于,所以函数的图像是有函数的图像向左平移个单位所得.由于零点都在某个区间上,所以函数的零点也在某个区间上.利用二分法的知识,计算的值,,且函数递增,有唯一零点在区间,左移个单位就是.
(三)分段函数的零点;
例3.已知函数,若关于的方程有8个不等的实数根,则的取值范围是
A. B. C. D.(2, )
【答案】D
【解析】函数,的图象如图:
关于的方程有8个不等的实数根, 必须有两个不相等的实数根,由函数图象可知,令,方程化为:, ,开口向下,对称轴为: ,可知: 的最大值为:, 的最小值为2, ,故选D.
练习1.函数的零点个数为( )
A.3 B.2 C.1 D.0
【答案】B
【解析】由得零点个数为2,选B.
(四)零点范围问题;
例4.【哈六中2019模拟】设函数,若方程恰好有三个根,且
,则的取值范围是( )
A. B. C. D.
【答案】B
【解析】由题意,则,
画出函数的大致图象:
由图得,当时,方程f(x)=a恰好有三个根,
由得,由得,
由图知,点与点关于直线对称,
点与点关于直线对称,
∴,则,
即的取值范围是[,),
故选B.
点睛:函数中方程问题,是高考经常涉及的重点问题,
(1)转化为函数的零点问题,研究函数的图象;
(2)分离参数后转化为函数的值域(最值)问题求解,如果涉及由几个零点时,还需考虑函数的图象与参数的交点个数;
(3)转化为两熟悉的函数图象的上、下关系问题,从而构建不等式求解.
练习1.已知函数,且存在不同的实数,使得,则的取值范围是( )
A. B.
C. D.
【答案】A
【解析】函数,画出的图象如图所示,作出直线,当时,直线与图象有三个交点,横坐标由小到大,设为,,,令,即,则有,令,得到,即有,
令,,,越大其值越大;,越大其值越大,则有,故选A.
(五)零点个数问题;
例5.【湖北2019模拟】定义在R上的奇函数满足①,②,③时,则函数的零点个数是( )
A.2 B.4 C.6 D.8
【答案】C
【解析】由①②可知,f(x)是周期为2的奇函数,又x∈[0,1]时,,
可得函数f(x)在R上的图象如图,
由图可知,函数y=f(x)−log3|x|的零点个数为6个,
本题选择C选项.
点睛:函数零点的求解与判断:
(1)直接求零点:令f(x)=0,如果能求出解,则有几个解就有几个零点.
(2)零点存在性定理:利用定理不仅要函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b
)<0,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点.
(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
练习1.关于的方程有三个不同实数解,则实数的取值范围是( )
A. B. C.(0, 3 ) D.
【答案】B
【解析】
,即为,
设,导数,
当时,在(1,+∞)递增;
当或时,在(−∞,0),(0,1)递减。
可得在处取得极小值3,
作出的图象,由题意可得当p>3时,
直线与有3个交点。
即有原方程有三个不同实数解,则的范围是.
练习2.已知函数,用表示中最小值,,则函数的零点个数为( )
A.1 B.2 C.3 D.4
【答案】C
【解析】由题意,作出的图象如图所示,由图象,得函数的零点有三个: ;故选C.
(六)零点与参数;
6.【2019南昌模拟】曲线与直线有两个交点时,实数的取值范围是
A. B. C. D.
【答案】A
【解析】可化为x2+(y﹣1)2=4,y≥1,所以曲线为以(0,1)为圆心,
2
为半径的圆y≥1的部分.直线y=k(x﹣2)+4过定点p(2,4),由图知,当直线经过A(﹣2,1)点时恰与曲线有两个交点,顺时针旋转到与曲线相切时交点边为一个.
且kAP=,由直线与圆相切得d=2,解得k=,
则实数k的取值范围为 ,
练习1.已知,又 ,若满足的
有四个,则的取值范围为( )
A. B. C. D.
【答案】A
练习2.若方程有大于2的根,则实数的取值范围是( )
A. B. C. D.
【答案】C
【解析】问题等价于方程在有解,而函数在上递增,值域为,所以k的取值范围是,故选C.
练习3.方程在区间上有根,则实数的取值范围为( )
A. B. C. D.
【答案】C
【解析】由于方程有解,设它的两个解分别为x1,x2,则x1⋅x2=−2<0,
故方程在区间[1,5]上有唯一解。
设f(x)= ,则有f(1)f(5)<0,即(a−1)(5a+23)⩽0,
解得: ⩽a⩽1,
故选:C.
点睛:已知函数有零点求参数取值范围常用的方法和思路
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
(七)零点与框图;
例7.二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入,则输出的值( )
A. B. C. D.
【答案】B
【解析】模拟程序的运行,可得
n=1,x1=1,x2=2,d=0.1,
令f(x)=x2−2,则f(1)=−1<0,f(2)=2>0,
m=1.5,f(1.5)=0.25>0,满足条件f(m)f(x1)<0,x2=1.5,
此时|1.5−1|=0.5>0.05,不合精确度要求。
n=2,m=1.25,f(1.25)=−0.4375<0.不满足条件f(m)f(x1)<0,x1=1.25,
此时|1.5−1.25|=0.25>0.05,不合精确度要求。
n=3,m=1.375,f(1.375)=−0.109<0.不满足条件f(m)f(x1)< 0,x1=1.375,
此时|1.5−1.375|=0.125>0.05,不合精确度要求。
n=4,m=1.375,f(1.4375)=0.066>0.满足条件f(m)f(x1)<0,x2=1.4375,此时|1.5−1.4375|=0.062>0.05,符合精确度要求。
n=5,m=1.4375,f(1.40625)=0.066<0.满足条件f(m)f(x1)<0,x1=1.40625,此时|1.5−1.4375|=0.03125<0.05,符合精确度要求。
退出循环,输出n的值为5.
本题选择B选项.
练习2.已知;;设函数,且函数的零点均在区间(,,)内,则的最小值为( )
A.8 B.9 C.10 D.11
【答案】C
【解析】∵,当时,,∴函数在区间上单调递增,故函数有唯一零点;∵,,当时,,∴函数在区间上单调递减,故函数有唯一零点;∴的零点在内,的零点在内,∵,且函数的零点均在区间(,,)内,因此的零点均在区间 内,∴的最小值为.故选C.
考点:1、利用导数研究函数的单调性;2、数列求和;3、函数零点存在性定理.
【思路点睛】利用导数分别求出函数、的零点所在的区间,然后要求的零点所在区间,即求的零点和的零点所在区间,根据图象平移即可求得结果.本题考查函数零点存在性定理和利用导数研究函数的单调性以及数列求和问题以及函数图象的平移,体现了分类讨论的思想,以及学生灵活应用知识分析解决问题的能力.属于中档题.
练习3.已知当表示不超过的最大整数,称为取整函数,例如,若,且偶函数,则方程的所有解之和为( )
A.1 B.-2 C. D.
【答案】D
【解析】设,则,又为偶函数,所以.由,得.在同一坐标系中画出与的图象,如图所示.由图知同,两个图象有四个交点,交点的纵坐标分别为,当时,方程的解是0和1;当时,由解得,由解得.综上,得的所有解之和为,故选D.