数学理卷·2018届北京市朝阳区高三第一学期期末质量检测（2018

数学理卷·2018届北京市朝阳区高三第一学期期末质量检测（2018

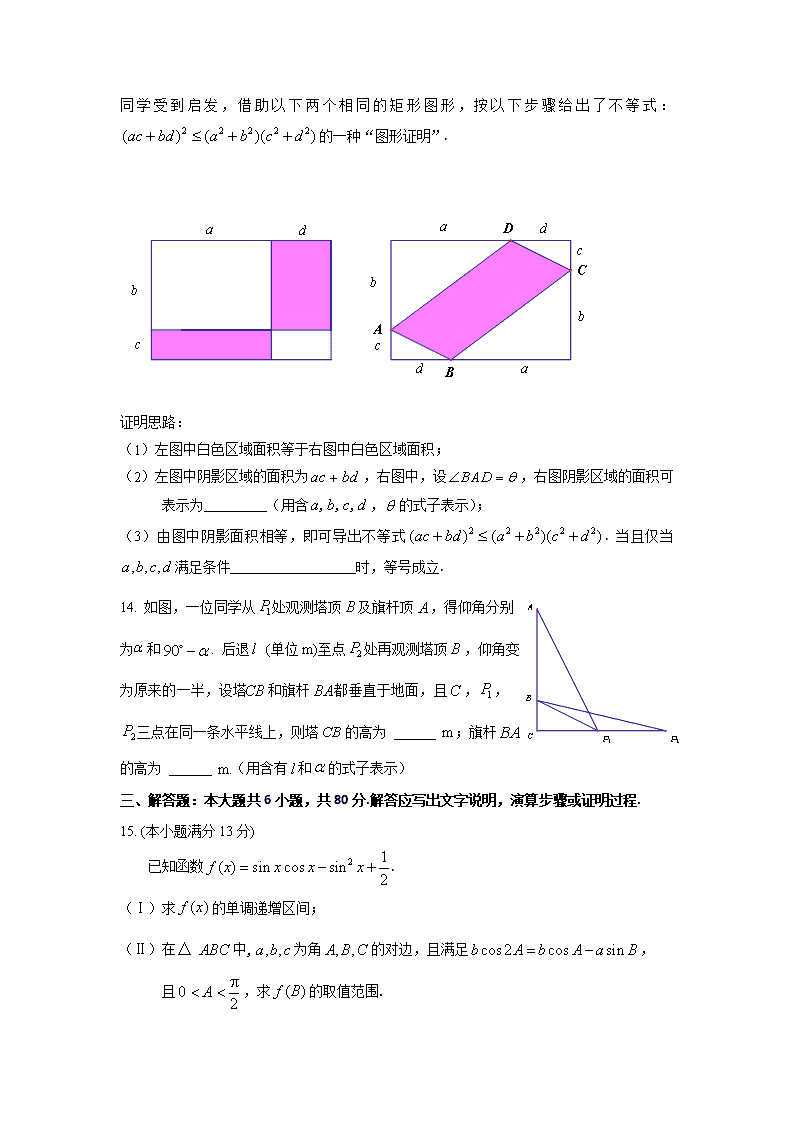
北京市朝阳区 2017-2018 学年度第一学期期末质量检测 数学试卷（理工类） 2018.1 （考试时间 120 分钟 满分 150 分） 本试卷分为选择题（共 40 分）和非选择题（共 110 分）两部分 第一部分（选择题 共 40 分） 一、选择题：本大题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，选出 符合题目要求的一项. 1. 已知集合 ， ，则 是 A. B. C. D. 2. 已知 为虚数单位，设复数 满足 ，则 = A. B. C. D. 3. 在平面直角坐标系中，以下各点位于不等式 表示的平面区域内 的是 A. B. C. D. 4.“ ”是“ ”的 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 5. 某四棱锥的三视图如图所示，格纸上小正方形的边长为 1， 则该四棱锥的体积为 A. B. C. D. 6. 已知圆 的圆心为 .直线 过点 且与 轴不重合， 交圆 于 两点，点 在点 ， 之间.过 作直线 的平行线交直线 于点 ，则点 的 轨迹是 { }| ( 2) 0A x x x= - < { }|ln 0B x x= > A B { }|1 2x x< < { }|0 2x x< < { }| 0x x > { }| 2x x > i z i 3z + = z 3 4 10 10 ( 2 1)( 3) 0x y x y+ − − + > (0 0)， ( 2 0)− ， (0 1)−， (0 2)， 2sin 2 α = cos2 =0α 4 4 3 4 2 3 4 2 2 2( 2) 9x y− + = C l ( 2,0)M − x l C ,A B A M B M AC BC P P A. 椭圆的一部分 B. 双曲线的一部分 C. 抛物线的一部分 D. 圆的一部分 7. 已知函数 的图象与直线 的公共点不少于两个，则实数 的取值范 围是 A. B. C. D. 8. 如 图 1 ， 矩 形 中 ， . 点 在 边 上 ， 且 . 如图 2 ， 沿直线 向上折起成 ．记二面角 的平面角为 ，当 时， ① 存在某个位置，使 ； ② 存在某个位置，使 ； ③ 任意两个位置，直线 和直线 所成的角都不相等. 以上三个结论中正确的序号是 A. ① B. ①② C. ①③ D. ②③ 第二部分（非选择题 共 110 分） 二、填空题：本大题共 6 小题，每小题 5 分，共 30 分.把答案填在答题卡上. 9. 已知中心在原点，焦点在坐标轴上的双曲线 的离心率为 ，则双曲线 的 渐近线方程为 . 10. 执行如图所示的程序框图，输出 的值为 . 11. 中， 分别为边 中点，若 （ ），则 _________. 12. 已 知 数 列 满 足 （ ）， ， ( ). 设 ，则 ; .（用含 的式子表示） 13. 伟大的数学家高斯说过：几何学唯美的直观能够帮助我们了解大自然界的基本问题.一位 C C ( )f x x x a= ⋅ − 1y = − a 2a < − 2a ≤ − 2 0a− ≤ < 2a > − ABCD 3AD = E AB CE DE⊥ 1AE = ADE△ DE 1A DE△ 1A DE A− − θ θ ( )00 180∈ ， 1CE DA⊥ 1DE AC⊥ DE 1AC 2 S  ABCD ,E F ,BC CD AF xAB yAE= +   ,x y ∈R + =x y { }na 1 1n n na a a+ −= − 2n ≥ 1a p= 2a q= ,p q∈R 1 n n i i S a = = ∑ 10a = 2018S = ,p q 图 1 BA E D C 开始 i=1，S=2 结束 i=i+1 i>4? 输出 S 是 否 S=i⋅ S E B CD A A1 图 2 同 学 受 到 启 发 ， 借 助 以 下 两 个 相 同 的 矩 形 图 形 ， 按 以 下 步 骤 给 出 了 不 等 式 ： 的一种“图形证明”. 证明思路： （1）左图中白色区域面积等于右图中白色区域面积； （2）左图中阴影区域的面积为 ，右图中，设 ，右图阴影区域的面积可 表示为_________（用含 ， 的式子表示）； （3）由图中阴影面积相等，即可导出不等式 . 当且仅当 满足条件__________________时，等号成立. 14. 如图，一位同学从 处观测塔顶 及旗杆顶 ，得仰角分别 为 和 . 后退 (单位 m)至点 处再观测塔顶 ，仰角变 为原来的一半，设塔 和旗杆 都垂直于地面，且 ， ， 三点在同一条水平线上，则塔 的高为 m；旗杆 的高为 m.（用含有 和 的式子表示） 三、解答题：本大题共 6 小题，共 80 分.解答应写出文字说明，演算步骤或证明过程. 15. (本小题满分 13 分) 已知函数 . （Ⅰ）求 的单调递增区间； （Ⅱ）在 中, 为角 的对边，且满足 ， 且 ，求 的取值范围. l α 2 2 2 2 2( ) ( )( )ac bd a b c d+ ≤ + + ac bd+ BAD θ∠ = a b c d, , , θ 2 2 2 2 2( ) ( )( )ac bd a b c d+ ≤ + + , , ,a b c d 1P B A α 90 α− l 2P B CB BA C 1P 2P CB BA 2 1( ) sin cos sin 2f x x x x= − + ( )f x △ ABC , ,a b c , ,A B C cos2 cos sinb A b A a B= − 0 2A π< < ( )f B A P2P1 B C b b d a c da c da c b D C B A 16. (本小题满分 13 分) 为了治理大气污染，某市 2017 年初采用了一系列措施，比如“煤改电”，“煤改气”，“国 Ⅰ，Ⅱ轻型汽油车限行”，“整治散乱污染企业”等.下表是该市 2016 年和 2017 年 12 月份的 空气质量指数（AQI）（AQI 指数越小，空气质量越好）统计表. 表 1：2016 年 12 月 AQI 指数表：单位（ ） 日期 1 2 3 4 5 6 7 8 9 10 11 AQI 47 123 232 291 78 103 159 132 37 67 204 日期 12 13 14 15 16 17 18 19 20 21 22 AQI 270 78 40 51 135 229 270 265 409 429 151 日期 23 24 25 26 27 28 29 30 31 AQI 47 155 191 64 54 85 75 249 329 表 2：2017 年 12 月 AQI 指数表：单位（ ） 日期 1 2 3 4 5 6 7 8 9 10 11 AQI 91 187 79 28 44 49 27 41 56 43 28 日期 12 13 14 15 16 17 18 19 20 21 22 AQI 28 49 94 62 40 46 48 55 44 74 62 日期 23 24 25 26 27 28 29 30 31 AQI 50 50 46 41 101 140 221 157 55 根据表中数据回答下列问题： （Ⅰ）求出 2017 年 12 月的空气质量指数的极差； （Ⅱ）根据《环境空气质量指数（AQI）技术规定（试行）》规定：当空气质量指数为 0～50 时，空气质量级别为一级.从 2017 年 12 月 12 日到 12 月 16 这五天中，随机抽取三天，空气 质量级别为一级的天数为 ，求 的分布列及数学期望； （Ⅲ）你认为该市 2017 年初开始采取的这些大气污染治理措施是否有效?结合数据说明理 由. 3g / mµ 3g / mµ ξ ξ 17. (本小题满分 14 分) 如图，在三棱柱 中， ， 是线段 的中点，且 平面 ． （Ⅰ）求证：平面 平面 ； （Ⅱ）求证： 平面 ； （ Ⅲ ） 若 ， ， 求 二 面 角 的余弦值. 18. (本小题满分 13 分) 已知函数 ， . （Ⅰ）求曲线 在点 处的切线的斜率； （Ⅱ）判断方程 （ 为 的导数）在区间 内的根的个数，说明理由； （Ⅲ）若函数 在区间 内有且只有一个极值点，求 的取值 范围. 1 1 1ABC ABC− 90ACB∠ =  D AC 1A D ⊥ ABC 1A BC ⊥ 1 1AAC C 1 //BC 1ABD 1 1AB AC⊥ 2AC BC= = 1A A B C− − ( ) cosf x x x a= + a∈R ( )y f x= 2x π= ( ) 0f x′ = ( )f x′ ( )f x ( )0,1 ( ) sin cosF x x x x ax= + + (0,1) a A C B B1 C1A1 D 19. (本小题满分 14 分) 已知抛物线 的焦点为 ,过抛物线 上的动点 （除顶点 外）作 的切 线 交 轴于点 .过点 作直线 的垂线 （垂足为 ）与直线 交于点 . （Ⅰ）求焦点 的坐标； （Ⅱ）求证： ； （Ⅲ）求线段 的长. 20. (本小题满分 13 分) 已 知 集 合 ， 其 中 . 表 示 中所有不同值的个数. （Ⅰ）若集合 ，求 ； （Ⅱ）若集合 ，求证： 的值两两不同，并求 ； （Ⅲ）求 的最小值.（用含 的代数式表示） :C 2 4x y= F C P O C l x T O l OM M PF N F FT MN FN { }1 2, ,..., nP a a a= ia ∈R ( )1 , 2i n n≤ ≤ > ( )M P +i ja a 1 )i j n≤ < ≤（ { }1,3,5 7,9P = ， ( )M P { }11,4,16,...,4nP −= +i ja a ( )M P ( )M P n 北京市朝阳区 2017-2018 学年度第一学期期末质量检测 高三年级数学试卷答案（理工类） 2018.1 一、选择题（40 分） 题号 1 2 3 4 5 6 7 8 答案 A C D A A B B C 二、填空题（30 分） 题号 9 10 11 答案 48 题号 12 13 14 答案 三、解答题（80 分） 15. （本小题满分 13 分） 解：（Ⅰ）由题知 . 由 （ ）， 解得 . 所以 单调递增区间为 （ ）. …………… 6 分 （Ⅱ）依题意，由正弦定理， . 因为在三角形中 ，所以 . 即 当 时， ； 当 时， . y x= ± 1 2 p− p q+ 2 2 2 2 sina b c d θ⋅ ⋅+ + ad bc= sinl α cos2 sin l α α 1 1 1( ) sin 2 (1 cos2 )2 2 2f x x x= − − + 1 1= sin 2 cos22 2x x+ 2= sin(2 )2 4x π+ 2 2 22 4 2k x k π π ππ − ≤ + ≤ π + k ∈Ζ 8 8k x k 3π ππ − ≤ ≤ π + ( )f x 3[ , ]8 8k k π ππ − π + k ∈Ζ sin cos2 sin cos sin sinB A B A A B= − sin 0B ≠ cos2 cos sinA A A= − (cos sin )(cos sin 1) 0A A A A− + − = cos sinA A= 4A π= cos sin 1A A+ = 2A π= 由于 ，所以 . 则 . 则 . 又 ， 所以 . 由 ， 则 的取值范围是 . ……………… 13 分 16. （本小题满分 13 分） 解：（Ⅰ）2017 年 12 月空气质量指数的极差为 194. …………………3 分 （Ⅱ） 可取 1，2，3 ； ； . 的分布列为 1 2 3 所以 . ………………9 分 （Ⅲ）这些措施是有效的.可以利用空气质量指数的平均数，或者这两年 12 月空气质量指数 为优的概率等来进行说明. ………………13 分 17. （本小题满分 14 分） （Ⅰ）证明：因为 ，所以 ． 根据题意， 平面 ， 平面 ，所以 ． 因为 ，所以 平面 ． 0 2A π< < 4A π= 3+ 4B C = π 30 4B< < π 24 4 4B π π 7π< + < 1 sin(2 ) 14B π− ≤ + ≤ 2( ) sin(2 )2 4f B B π= + ( )f B 2 2 2 2  −    ， ξ 1 2 3 2 3 5 3( 1) 10 C CP C ξ = = = 2 1 3 2 3 5 6( 2) 10 C CP C ξ = = = 3 0 3 2 3 5 1( 3) 10 C CP C ξ = = = ξ ξ P 3 10 6 10 1 10 3 6 11 2 3 1.810 10 10Eξ = × + × + × = 90ACB∠ =  BC AC⊥ 1A D ⊥ ABC BC ⊂ ABC 1A D BC⊥ 1AD AC D= BC ⊥ 1 1AAC C 又因为 平面 ，所以平面 平面 ． ………………4 分 （Ⅱ）证明：连接 ，设 ，连接 ． 根据棱柱的性质可知， 为 的中点， 因为 是 的中点， 所以 ． 又因为 平面 ， 平面 ， 所以 平面 ． ………………8 分 （Ⅲ）如图，取 的中点 ，则 ， 因为 ，所以 ， 又因为 平面 ， 所以 两两垂直． 以 为原点，分别以 为 轴建立空间坐标系（如图）. 由（Ⅰ）可知， 平面 , 所以 ． 又因为 ， , 所以 平面 ，所以 ， 所以四边形 为菱形． 由已知 ， 则 ， ， ， ． 设平面 的一个法向量为 ， 因为 ， ，所以 ，即 BC ⊂ 1A BC 1A BC ⊥ 1 1AAC C 1AB 1 1AB AB E= DE E 1AB D AC 1//DE BC DE ⊂ 1ABD 1B C ⊄ 1ABD 1 //BC 1ABD AB F //DF BC BC AC⊥ DF AC⊥ 1A D ⊥ ABC 1, ,DF DC DA D 1, ,DF DC DA , ,x y z BC ⊥ 1 1AAC C 1BC AC⊥ 1 1AB AC⊥ 1BC A B B= 1AC ⊥ 1A BC 1 1AC AC⊥ 1 1AAC C 2AC BC= = ( )0, 1,0A − ( )0,1,0C ( )2,1,0B ( )1 0,0, 3A 1A AB ( ), ,x y z=n ( )1 0,1, 3AA = ( )2,2,0AB = 1 0, 0, AA AB  ⋅ = ⋅ =   n n 3 0, 2 2 0. y z x y  + = + = A C B B1 C1A1 D E y x z A C B B1 C1A1 D F 设 ，则 ． 再设平面 的一个法向量为 ， 因为 ， ，所以 ，即 设 ，则 ． 故 ． 由图知，二面角 的平面角为锐角， 所以二面角 的余弦值为 ． …………14 分 18. （本小题满分 13 分） 解：（Ⅰ） . . …………3 分 （Ⅱ）设 ， . 当 时， ，则函数 为减函数. 又因为 ， , 所以有且只有一个 ，使 成立. 所以函数 在区间 内有且只有一个零点.即方程 在区间 内有 且只有一个实数根. ……………7 分 （ Ⅲ ） 若 函 数 在 区 间 内 有 且 只 有 一 个 极 值 点 ， 由 于 ，即 在区间 内有且只有一个零点 ，且 在 两侧异号. 因为当 时，函数 为减函数，所以在 上， ， 即 成立，函数 为增函数； 在 上， ，即 成立，函数 为减函数, ( ) sin cosF x x x x ax= + + ( )0,1 ( ) ( )F x f x′ = ( ) cosf x x x a= + ( )0,1 1x ( )f x 1x (0,1)x∈ ( )g x ( )00, x 0( ) ( ) 0g x g x> = ( ) 0f x′ > ( )f x 0( ,1)x 0( ) ( ) 0g x g x< = ( ) 0f x′ < ( )f x 1z = ( )3, 3,1= −n 1A BC ( )1 1 1, ,x y z=m ( )1 0, 1, 3CA = − ( )2,0,0CB = 1 0, 0, CA CB  ⋅ = ⋅ =   m m 1 1 1 3 0, 2 0. y z x − + = = 1 1z = ( )0, 3,1=m 3 1 7cos , 77 2 ⋅ − +〈 〉 = = =⋅ × m nm n m n 1A A B C− − 1A A B C− − 7 7 ( ) cos sinf x x x x′ = − π π( )2 2k f ′= = − ( ) ( )g x f x′= ( ) sin (sin cos ) 2sin cosg x x x x x x x x′ = − − + = − − (0,1)x∈ ( ) 0g x′ < ( )g x (0) 1 0g = > (1) cos1 sin1 0g = − < 0 (0,1)x ∈ 0( ) 0g x = ( )g x ( )0,1 ( ) 0f x′ = ( )0,1 则函数 在 处取得极大值 . 当 时，虽然函数 在区间 内有且只有一个零点 ，但 在 两侧同号，不满足 在区间 内有且只有一个极值点的要求. 由于 ，显然 . 若函数 在区间 内有且只有一个零点 ，且 在 两侧异号， 则只需满足： 即 解得 . ……………13 分 19. （本小题满分 14 分） 解：（Ⅰ） ……………2 分 （ Ⅱ ） 设 . 由 ， 得 ， 则 过 点 的 切 线 的 斜 率 为 . 则过点 的切线 方程为 .令 ，得 ，即 .又点 为抛物线上除顶点 外的动点， ，则 .而由已知得 ，则 . 又 ，即 与 不重合， 即 . …………6 分 （ Ⅲ ） 由 ( Ⅱ ) 问 ， 直 线 的 方 程 为 ， . 直 线 的 方 程 为 ， . 设 和 交 点 的 坐 标 为 则 ( )f x 0x x= 0( ) 0f x = ( )f x ( )0,1 0x ( )f x 0x ( )F x ( )0,1 (1) cos1f a= + ， (0)f a= (1) (0)f f> ( )f x ( )0,1 1x ( )f x 1x cos1 0a− ≤ < 0( )f x (0) 0 , (1) 0 , f f <  ≥ 0, cos1 0, a a <  + ≥ (0,1)F 0 0( , )P x y 2 4x y= 21 4y x= P l 0 0 1 2x xk y x=′= = P l 2 0 0 1 1 2 4y x x x= − 0y = 0 1 2Tx x= 0 1( ,0)2T x P O 0 0x ≠ 0 2 TFk x = − MN l⊥ 0 2 MNk x = − 0 0x ≠ FT MN FT MN MN 0 2y xx = − 0 0x ≠ PF 0 0 11 yy xx −− = 0 0x ≠ MN PF N ( , )N NN x y 由（1）式得， （由于 不与原点重合，故 ）.代入（2），化简得 .又 ，化简得, （ ）. 即点 在以 为圆心，1 为半径的圆上.（原点与 除外） 即 . …………14 分 20. （本小题满分 13 分） 解：（Ⅰ） ； ………… 3 分 （Ⅱ）形如和式 共有 项，所以 . 对于集合 中的和式 ， ： 当 时， 时， ； 当 时，不妨设 ，则 . 所以 的值两两不同. 且 . ………… 8 分 （Ⅲ）不妨设 ，可得 . 中至少有 个不同的数. 即 . 设 成等差数列， ， 则对于每个和式 ，其值等于 （ ）或 中的一个.去掉重复的一个 , 0 0 0 2 .........(1) 1 1 ..........(2) N N N N y xx yy xx  = − − = + 0 2 N N xx y = − N 0Ny ≠ 0 2 N N yy y −= ( )0Ny ≠ 2 0 04x y= 2 2( 1) 1N Nx y+ − = 0Nx ≠ N F ( )0,2 1FN = ( )=7M P +i ja a 1 )i j n≤ < ≤（ 2 ( 1) 2n n nC −= ( 1)( ) 2 n nM P −≤ { }11,4,16,...,4n− +i ja a +p qa a 1 ,1 )i j n p q n≤ < ≤ ≤ < ≤（ j q= i p≠ + +i j p qa a a a≠ j q≠ j q< 1 2 1+ 2 4 j i j j j q p qa a a a a a a − +< = < ≤ < + +i ja a 1 )i j n≤ < ≤（ ( 1)( )= 2 n nM P − 1 2 3 ... na a a a< < < < 1 2 1 3 1 2 1+ + ... + + ... +n n n na a a a a a a a a a−< < < < < < +i ja a 1 )i j n≤ < ≤（ 2 3n − ( ) 2 3M P n≥ − 1 2, ,..., na a a 1 1 , ( ) + = , ( ) i j n n i j i j a a i j n a a a a i j n + − + − + + > + + ≤ +i ja a 1 )i j n≤ < ≤（ 1+ pa a 2 p n≤ ≤ +q na a (1 1)q n≤ ≤ − 1 na a+ 所以对于这样的集合 , . 则 的最小值为 . ……………13 分 P ( ) 2 3M P n= − ( )M P 2 3n −