高考数学函数零点专题

高考数学函数零点专题

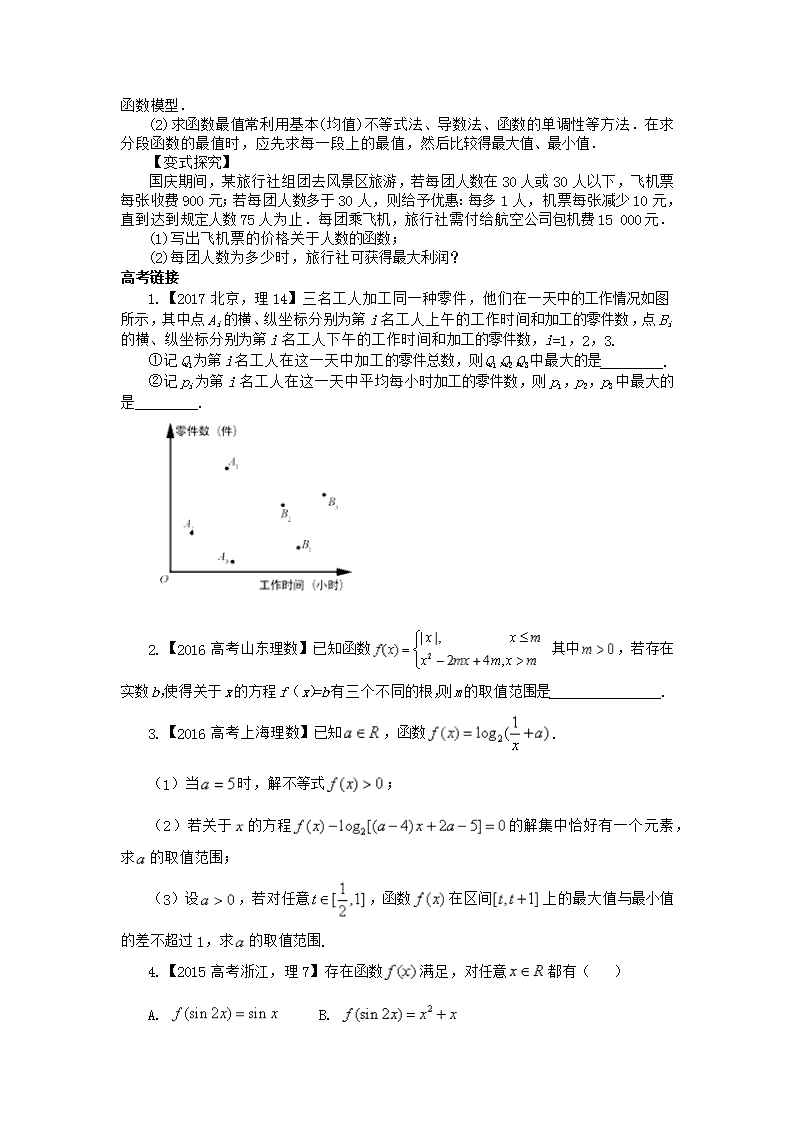
专题2.函数的零点 高考解读 求方程的根、函数的零点的个数问题以及由零点存在性定理判断零点是否存在，利用函数模型解决实际问题是高考的热点；备考时应理解函数的零点，方程的根和函数的图象与x轴的交点的横坐标的等价性；掌握零点存在性定理．增强根据实际问题建立数学模型的意识，提高综合分析、解决问题的能力．‎ 知识梳理 ‎1．函数的零点与方程的根 ‎(1)函数的零点 对于函数f(x)，我们把使f(x)＝0的实数x叫做函数f(x)的零点．‎ ‎(2)函数的零点与方程根的关系 函数F(x)＝f(x)－g(x)的零点就是方程f(x)＝g(x)的根，即函数y＝f(x)的图象与函数y＝g(x)的图象交点的横坐标．‎ ‎(3)零点存在性定理 如果函数y＝f(x)在区间[a，b]上的图象是连续不断的一条曲线，且有f(a)·f(b)<0，那么，函数y＝f(x)在区间(a，b)内有零点，即存在c∈(a，b)使得f(c)＝0, 这个c也就是方程f(x)＝0的根．注意以下两点：①满足条件的零点可能不唯一；②不满足条件时，也可能有零点．‎ ‎(4)二分法求函数零点的近似值，二分法求方程的近似解．‎ ‎2．在求方程解的个数或者根据解的个数求方程中的字母参数的范围的问题时，数形结合是基本的解题方法，即把方程分拆为一个等式，使两端都转化为我们所熟悉的函数的解析式，然后构造两个函数f(x)，g(x)，即把方程写成f(x)＝g(x)的形式，这时方程根的个数就是两个函数图象交点的个数，可以根据图象的变化趋势找到方程中字母参数所满足的各种关系.‎ 高频考点突破 考点一 函数的零点判断 例1、【2017课标3，理11】已知函数有唯一零点，则a=‎ A． B． C． D．1‎ ‎【变式探究】(1)函数f(x)＝ex＋x－2的零点所在的区间是(　　)‎ A. B. C．(1,2) D．(2,3)‎ ‎(2)已知偶函数y＝f(x)，x∈R满足：f(x)＝x2－3x(x≥0)，若函数g(x)＝则y＝f(x)－g(x)的零点个数为(　　)‎ A．1 B．3 C．2 D．4‎ ‎【方法技巧】函数零点的求法 ‎(1)直接求零点：令f(x)＝0，如果能求出解，则有几个解就有几个零点．‎ ‎(2)零点存在性定理：利用定理不仅要函数在区间[a，b]上是连续不断的曲线，且f(a)·f(b)<0，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．‎ ‎(3)利用图象交点的个数：将函数变形为两个函数的差，画两个函数的图象，看其有几个交点，就有几个不同的零点．‎ ‎【变式探究】设f(x)＝ln x＋x－2，则函数f(x)的零点所在的区间为(　　)‎ A．(0,1) B．(1,2) C．(2,3) D．(3,4)‎ 考点二、二次函数的零点 例2、已知函数f(x)＝x2＋ax＋2，a∈R.‎ ‎(1)若不等式f(x)≤0的解集为[1,2]，求不等式f(x)≥1－x2的解集；‎ ‎(2)若函数g(x)＝f(x)＋x2＋1在区间(1,2)上有两个不同的零点，求实数a的取值范围．‎ ‎【方法技巧】‎ 解决二次函数的零点问题：(1)可利用一元二次方程的求根公式；(2)可用一元二次方程的判别式及根与系数之间的关系；(3)利用二次函数的图象列不等式组．‎ ‎【变式探究】‎ 已知f(x)＝x2＋(a2－1)x＋(a－2)的一个零点比1大，一个零点比1小，求实数a的取值范围．‎ 考点三 函数零点的应用 例3、【2017课标1，理21】已知函数.‎ ‎（1）讨论的单调性；‎ ‎（2）若有两个零点，求a的取值范围.‎ ‎【变式探究】已知函数f(x)＝函数g(x)＝b－f(2－x)，其中b∈R.若函数y＝f(x)－g(x)恰有4个零点，则b的取值范围是(　　)‎ A. B. C. D.‎ ‎【方法规律】‎ 函数零点的应用主要表现在利用零点求参数范围，若方程可解，通过解方程即可得出参数的范围，若方程不易解或不可解，则将问题转化为构造两个函数，利用两个函数图象的关系求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用．‎ ‎【变式探究】‎ 对于实数m，n定义运算“⊕”：m⊕n＝设f(x)＝(2x－1)⊕(x－1)，且关于x的方程f(x)＝a恰有三个互不相等的实数根x1，x2，x3，则x1＋x2＋x3的取值范围是________．‎ 考点四、分段函数的模型 例4、【2017课标3，理15】设函数则满足的x的取值范围是_________.‎ ‎【变式探究】已知一家公司生产某品牌服装的年固定成本为10万元，每生产1千件需另投入2.7万元．设该公司一年内共生产该品牌服装x千件并全部销售完，每千件的销售收入为R(x)万元，且R(x)＝ ‎(1)写出年利润W(万元)关于年产量x(千件)的函数解析式；‎ ‎(2)年产量为多少千件时，该公司在这一品牌服装的生产中所获得的年利润最大？(注：年利润＝年销售收入－年总成本)‎ ‎【方法技巧】‎ ‎(1)很多实际问题中，变量间的关系不能用一个关系式给出，这时就需要构建分段函数模型．‎ ‎(2)求函数最值常利用基本(均值)不等式法、导数法、函数的单调性等方法．在求分段函数的最值时，应先求每一段上的最值，然后比较得最大值、最小值．‎ ‎【变式探究】‎ 国庆期间，某旅行社组团去风景区旅游，若每团人数在30人或30人以下，飞机票每张收费900元；若每团人数多于30人，则给予优惠：每多1人，机票每张减少10元，直到达到规定人数75人为止．每团乘飞机，旅行社需付给航空公司包机费15 000元．‎ ‎(1)写出飞机票的价格关于人数的函数；‎ ‎(2)每团人数为多少时，旅行社可获得最大利润？‎ 高考链接 ‎1.【2017北京，理14】三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中点Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数，点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数，i=1，2，3.‎ ‎①记Q1为第i名工人在这一天中加工的零件总数，则Q1，Q2，Q3中最大的是_________.‎ ‎②记pi为第i名工人在这一天中平均每小时加工的零件数，则p1，p2，p3中最大的是_________.‎ ‎2.【2016高考山东理数】已知函数 其中，若存在实数b，使得关于x的方程f（x）=b有三个不同的根，则m的取值范围是________________.‎ ‎3.【2016高考上海理数】已知，函数.‎ ‎（1）当时，解不等式；‎ ‎（2）若关于的方程的解集中恰好有一个元素，求的取值范围；‎ ‎（3）设，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.‎ ‎4.【2015高考浙江，理7】存在函数满足，对任意都有（ ）‎ A. B. ‎ C. D. ‎ ‎5.【2015高考湖南，理15】已知，若存在实数，使函数有两个零点，则的取值范围是 .‎ ‎6.【2015高考江苏，13】已知函数，，则方程实根的个数为 ‎ ‎7.【2015高考天津，理8】已知函数 函数 ，其中，若函数 恰有4个零点，则的取值范围是( )‎ ‎（A） （B） （C） （D）‎ ‎8.【2015高考浙江，理10】已知函数，则 ，的最小值是 ．‎ ‎9.【2015高考四川，理13】某食品的保鲜时间y（单位：小时）与储存温度x（单位：）满足函数关系（为自然对数的底数，k、b为常数）。若该食品在0的保鲜时间设计192小时，在22的保鲜时间是48小时，则该食品在33的保鲜时间是 小时。‎ ‎10.【2015高考上海，理10】设为，的反函数，则的最大值为 ．‎ ‎12.【2015高考浙江，理18】已知函数，记是在区间上的最大值.‎ （1） 证明：当时，；‎ ‎（2）当，满足，求的最大值.‎ ‎13.（2014·湖南卷）某市生产总值连续两年持续增加，第一年的增长率为p，第二年的增长率为q，则该市这两年生产总值的年平均增长率为(　　)‎ A. B.C. D.－1‎ ‎14．（2014·湖南卷）已知函数f(x)＝x2＋ex－(x<0)与g(x)＝x2＋ln(x＋a)的图像上存在关于y轴对称的点，则a的取值范围是(　　)‎ A．(－∞，) B．(－∞，)C. D. ‎15.（2014·天津卷）已知函数f(x)＝|x2＋3x|，x∈R.若方程f(x)－a|x－1|＝0恰有4个互异的实数根，则实数a的取值范围为________．‎ ‎16．（2014·浙江卷）已知函数f(x)＝x3＋ax2＋bx＋c，且09‎ ‎17.（2014·全国卷）若函数f(x)＝cos 2x＋asin x在区间是减函数，则a的取值范围是________．‎ ‎　　　　C　　　　　　　　　　　D ‎18．（2014·江西卷）已知函数f(x)＝5|x|，g(x)＝ax2－x(a∈R)．若f[g(1)]＝1，则a＝(　　)‎ A．1 B．2 C．3 D．－1‎ ‎19．（2014·辽宁卷）已知a＝2－，b＝log2，c＝log，则(　　)‎ A．a>b>c B．a>c>b ‎ C．c>a>b D．c>b>a ‎20．（2014·山东卷）已知实数x，y满足ax＜ay(0＜a＜1)，则下列关系式恒成立的是(　　)‎ A. ＞ B. ln(x2＋1)＞ln(y2＋1) C. sin x＞sin y D. x3＞y3‎