2018-2019学年吉林省汪清县第六中学高二上学期期中考试数学（理）试题 解析版

2018-2019学年吉林省汪清县第六中学高二上学期期中考试数学（理）试题 解析版

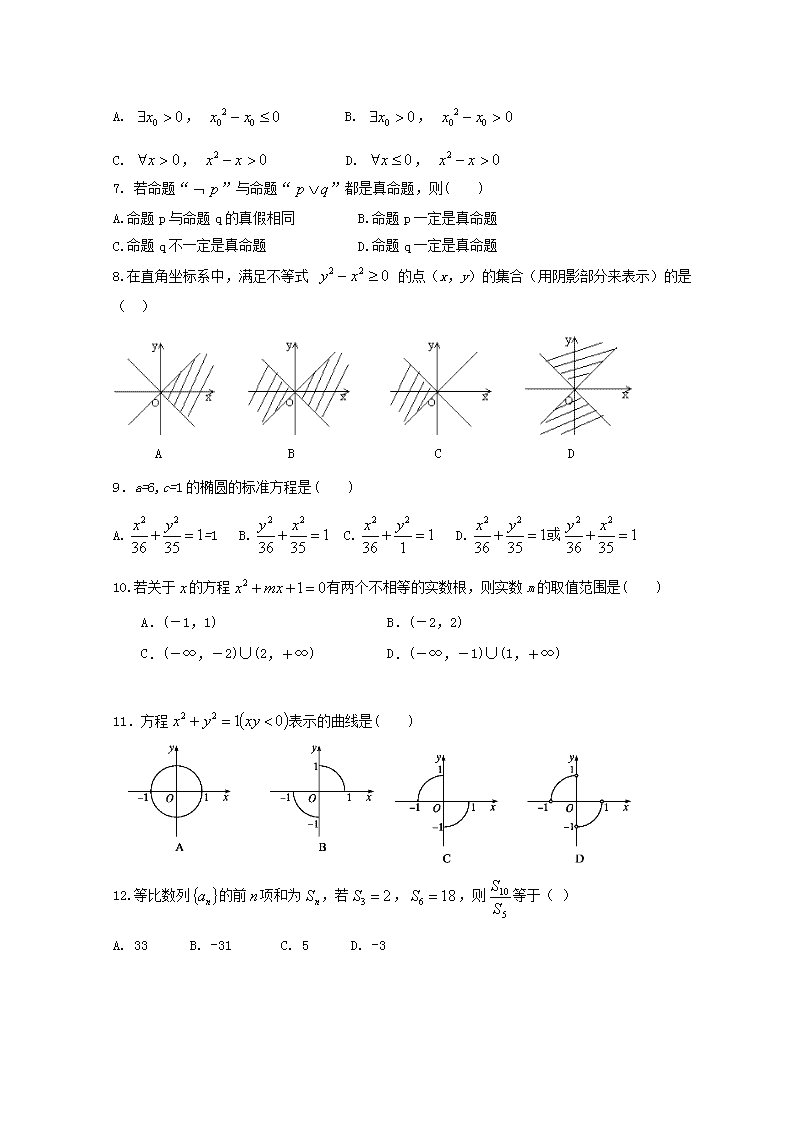
‎2018-2019学年度第一学期汪清六中期中考试 高二理科数学试题 考试时间：120分钟；命题人： 李玲玲 姓名：__________班级：__________‎ 题号 一 二 三 总分 得分 注意事项：‎ ‎1. 答题前填写好自己的姓名、班级、考号等信息 ‎2. 请将答案正确填写在答题卡上 评卷人 得分 一、填空题（每小题5分，共60分）‎ ‎1．如果，那么下列不等式一定成立的是（ ）‎ A. B. C. D. ‎ ‎2．已知是等差数列的第项，则（ ）‎ A. B. C. D.‎ ‎3．点A(－2，b)不在平面区域2x－3y＋5≥0内，则b的取值范围是(　　)‎ A．b≤ B．b＜1 C．b＞ D．b＞－9‎ ‎4．命题：“若，则且”的逆否命题是（　　）‎ A. 若，则且 B. 若，则或 C. 若或，则 D. 若且，则 ‎ ‎5．“常数是与的等比中项”是“”的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎6.命题“， ”的否定是（ ）‎ A. ， B. ， ‎ C. ， D. ， ‎ ‎7. 若命题“”与命题“”都是真命题，则(　　)‎ A.命题p与命题q的真假相同 B.命题p一定是真命题 C.命题q不一定是真命题 D.命题q一定是真命题 ‎8.在直角坐标系中，满足不等式 的点（x，y）的集合（用阴影部分来表示）的是（　）‎ ‎ ‎ ‎ A B C D ‎9．a=6,c=1的椭圆的标准方程是(　　)‎ A.=1 B. C. D.或 ‎10.若关于的方程有两个不相等的实数根，则实数m的取值范围是(　　)‎ A．(－1，1) B．(－2，2)‎ C．(－∞，－2)∪(2，＋∞) D．(－∞，－1)∪(1，＋∞)‎ ‎11．方程表示的曲线是(　　)‎ ‎ ‎ ‎12.等比数列的前项和为，若，，则等于（ ）‎ A. 33 B. -31 C. 5 D. -3 ‎ ‎ ‎ 评卷人 得分 二、填空题（每小题5分，共20分）‎ ‎13.在命题“若，则”的逆命题、否命题、逆否命题中,假命题的个数是　　　　.‎ ‎14．已知数列的前项和为，且，则__________．‎ ‎15.设x，y满足约束条件则z＝2x－3y的最大值是_______．‎ ‎16. 若直线， 过点，则的最小值为__________．‎ 评卷人 得分 三、解答题（共70分）‎ ‎17.解下列不等式并将结果用集合的形式表示。‎ ‎⑴⑵‎ ‎18．已知是递增的等差数列，是方程的根。‎ ‎（1）求的通项公式；‎ ‎（2）求数列的前项和.‎ ‎19．(1)已知x>2，求x＋的最小值；‎ ‎(2)设00时,y<0,曲线应在第四象限;‎ 当x<0时,y>0,曲线应在第二象限,且与坐标轴均无交点.‎ 答案:D ‎12.【答案】A ‎ ‎【解析】等比数列中，，所以.‎ 所以.‎ ‎.‎ 故选A.‎ ‎13.解析:原命题为假命题,逆否命题也为假命题,逆命题也是假命题,否命题也是假命题.故假命题个数为3.‎ 答案:3‎ ‎14.【答案】14‎ ‎【解析】由题意得．‎ 答案： ‎ ‎15.【答案】12‎ ‎【解析】不等式组表示的平面区域如图所示,‎ 当直线z＝2x－3y经过点A时,在y轴上的截距最小,由解得A(3,-2),代入得z＝2x－3y的最大值是12,故填12.‎ ‎16.【答案】8‎ ‎【解析】∵直线过点 ‎∴‎ ‎∴‎ ‎∵‎ ‎∴，当且仅当，即， 时取等号 ‎∴的最小值为8‎ ‎17.【答案】⑴（-3，1）⑵‎ 试题分析：（1）化为，利用一元二次不等式的解法即可得出；（2）化为，解出即可.‎ 试题解析：（1）﹣x2﹣2x+3＞0化为x2+2x﹣3＜0，解得﹣3＜x＜1，‎ ‎∴不等式的解集为（﹣3，1）；‎ ‎（2）化为？，‎ 解得x≥2或x＜﹣1.‎ ‎∴不等式的解集为{x|x≥2或x＜﹣1|}．‎ ‎18.【答案】(1);(2).‎ 试题分析：(1)先求出二次方程的根,再根据等差数列的通项公式求出;(2)由等差数列的求和公式计算即可.‎ 试题解析:‎ ‎（1）因为方程的两根为，‎ 所以由题意 所以等差数列的公差，首项 所以数列的通项公式为.‎ ‎(2)由（1）有.‎ ‎19.解：(1)∵x>2，∴x－2>0，‎ ‎∴x＋＝x－2＋＋2≥2 ＋2＝6，‎ 当且仅当x－2＝，‎ 即x＝4时，等号成立.∴x＋的最小值为6.‎ ‎(2)∵00，‎ ‎∴y＝4x(3－2x)＝2[2x(3－2x)]≤22＝.‎ 当且仅当2x＝3－2x，即x＝时，等号成立.‎ ‎∵∈，‎ ‎∴函数y＝4x(3－2x)的最大值为.‎ ‎20.设点M的坐标为(x,y).‎ ‎∵直线MA与MB的斜率之积为-1,∴直线MA,MB都存在斜率,∴x≠0.‎ 由A(0,-4),B(0,4),得kMA=,kMB=.‎ 又kMA·kMB=-1,‎ ‎∴=-1,化简得x2+y2=16.‎ 故点M的轨迹方程为x2+y2=16(x≠0).‎ ‎21.（1）因为ax2＋bx＋2＞0的解集为{x|－1＜x＜2}，‎ 所以解得 ‎（2）由（1）得bx2－ax－2＞0，即x2＋x－2＞0，‎ 解得x＞1或x＜－2.‎ 所以，解集为{x|x＞1或x＜－2}‎ ‎22.【答案】（1）；（2）.‎ 试题分析：‎ ‎(1)由题意求得首项和公比，则数列的通项公式为；‎ ‎(2)结合(1)的结果错位相减可得.‎ 试题解析：‎ ‎（1）设正项等比数列的公比为，若，则，不符合题意；则∴，解得：‎ ‎∴（2）①‎ ‎②‎ ‎①②得：‎ ‎∴‎