- 2021-04-13 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2018届山东省泰安三中、新泰二中、宁阳二中三校高二下学期期中联考(2017-04)
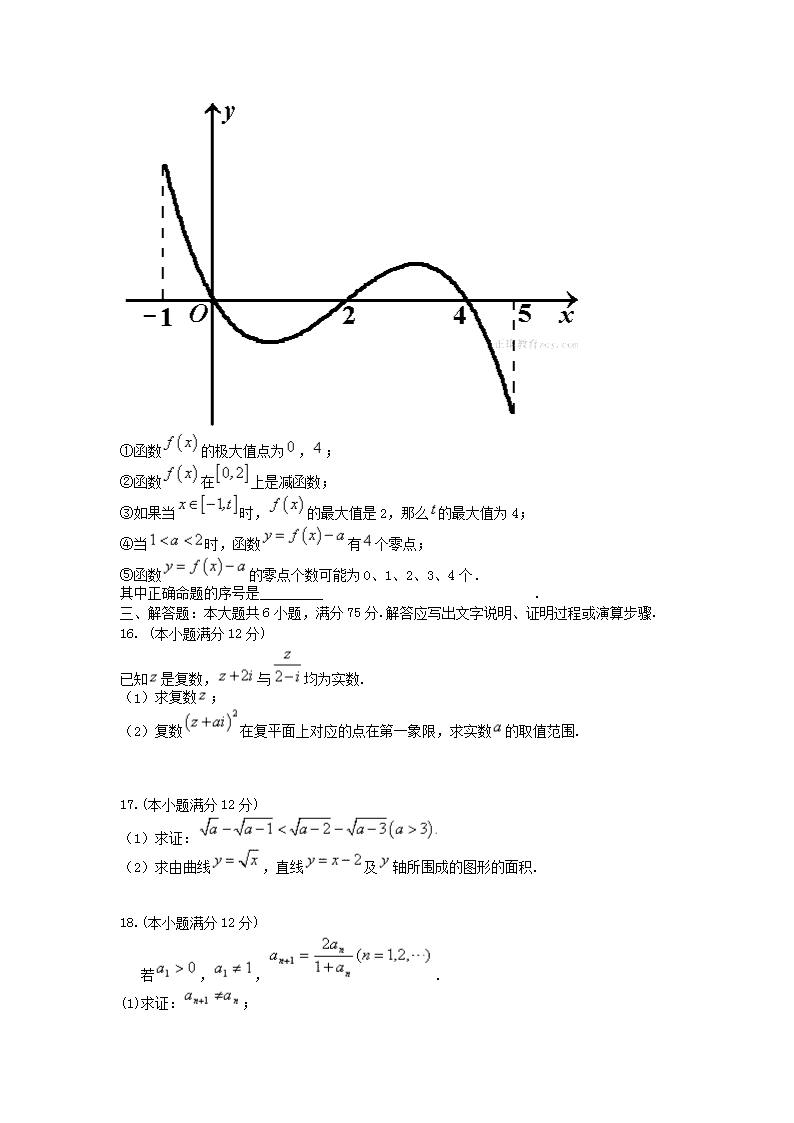
泰安三中、新泰二中、宁阳二中高二期中考试 数学(理科)试卷 一、选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数所对应的的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.函数f(x)=(x-3)ex的单调递增区间是( ) A.(-∞,2) B.(0,3) C.(1,4) D.(2,+∞) 3.用数学归纳法证明+++…+<1(n∈N*,n≥2),由“k到k+1”时,不等式左端的变化是( ) A.增加一项 B.增加和两项 C.增加和两项,同时减少一项 D.以上都不对 4.设P为曲线C:上的点,且曲线C在点P处切线倾斜角的取值范围为,则点P横坐标的取值范围为( ) A. B. C. D. 5.若在上是减函数,则实数的取值范围是( ) A. B. C. D. 6.用反证法证明命题“三角形的内角中至少有一个角不大于60°”时,应假设( ) A.三角形的三个内角都不大于60° B.三角形的三个内角都大于60° C.三角形的三个内角至多有一个大于60° D.三角形的三个内角至少有两个大于60° 7.有一段“三段论”,其推理是这样的“对于可导函数,若,则是函数的极值点,因为函数满足,所以是函数的极值点”,以上推理( ) A.大前提错误 B.小前提错误 C.推理形式错误 D.没有错误 8.设<b,函数的图像可能是( ) 9.观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10 +b10=( ) A.28 B.76 C.99 D.123 10.设函数在上的导函数为,在上的导函数为,若在上,恒成立,则称函数函数在上为“凸函数”.已知当时,在上是“凸函数”.则在上( ) A.既有极大值,也有极小值 B.有极大值,没有极小值 C.没有极大值,有极小值 D.没有极大值,也没有极小值 二、填空题:本大题共4小题,每小题5分,满分20分. 11.计算: _________ 12.设复数z满足,其中i为虚数单位,则z的共轭复数_________ 13..设曲线在点处的切线与直线垂直,则等于_________ . 14. 1 如图,它满足: 2 2 ①第n行首尾两数均为n, 3 4 3 ②表中的递推关系类似杨辉三角, 4 7 7 4 则第n行第2个数是_________ 5 11 14 11 5 6 16 25 25 16 6 15..已知函数的定义域为,部分对应值如下表,的导函数的图象如图所示. 下列关于的命题: ①函数的极大值点为,; ②函数在上是减函数; ③如果当时,的最大值是2,那么的最大值为4; ④当时,函数有个零点; ⑤函数的零点个数可能为0、1、2、3、4个. 其中正确命题的序号是_________ . 三、解答题:本大题共6小题,满分75分.解答应写出文字说明、证明过程或演算步骤. 16. (本小题满分12分) 已知是复数,与均为实数. (1)求复数; (2)复数在复平面上对应的点在第一象限,求实数的取值范围. 17.(本小题满分12分) (1)求证: (2)求由曲线,直线及轴所围成的图形的面积. 18.(本小题满分12分) 若,,. (1)求证:; (2)令写出的值,观察并归纳出这个数列的通项公式, 并用数学归纳法证明. 19.(本小题满分12分) 已知x=3是函数f(x)=aln(1+x)+x2-10x的一个极值点. (1) 求a; (2) 求函数f(x)的单调区间; (3) 若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围. 20.(本小题满分13分) 时下,网上教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量(单位:千套)与销售价格(单位:元/套)满足的关系式为,其中,为常数.已知销售价格为4元/套时,每日可售出套题21千套. (1)求的值; (2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑售出的套数),试确定销售价格的值,使网校每日销售套题所获得的利润最大.(保留1位小数点) 21.(本小题满分14分) 已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2. (1)若曲线f(x)=xlnx在x=1处的切线与函数g(x)=﹣x2+ax﹣2也相切,求实数a的值; (2)求函数f(x)在上的最小值; (3)证明:对任意的x∈(0,+∞),都有成立 参考答案 DDCAD BACDB 11.e2-e-ln2 12 13 14 15 ①②⑤ 三、 16. 解:(Ⅰ)设, 为实数, . ………………………………3分 为实数, ,则.………………………………6分 (Ⅱ)在第一象限, ………………………………9分 解得.…………………………12分 17. (Ⅰ)证明:∵, ∴ ∴ ∴ 6分 (Ⅱ)解:联立方程得到两曲线的交点,因此曲线,直线及轴所围成的图形的面积为 12分 18解:(1)证明:假设,即, 解得 ………2分 从而, 这与题设相矛盾, ………………4分 所以不成立.故成立. ………………5分 (2)由题意得,………………6分 由此猜想:. ………………8分 ………………9分 19(1) 因为f′(x)=+2x-10 所以f′(3)=+6-10=0 因此a=16 (2) 由(1)知,f(x)=16ln(1+x)+x2-10x, x∈(-1,+∞) f′(x)= 当x∈(-1,1)∪(3,+∞)时,f′(x)>0 当x∈(1,3)时,f′(x)<0 所以f(x)的单调增区间是(-1,1),(3,+∞) f(x)的单凋减区间是(1,3) (3) 由(2)知,f(x)在(-1,1)内单调增,在(1,3)内单调减,在(3,+∞)上单调增, 所以f(x)的极大值为f(1)=16ln2-9,极小值为f(3)=32ln2-21 又x→-1时,f(x)→-∞; x→+∞时,f(x)→+∞; 可据此画出函数y=f(x)的草图,由图可知 要使直线y=b与y=f(x)的图象各有3个交点,则f(3)<b<f(1) 所以b的取值范围为(32 ln2-21,16ln2-9). 20解:(Ⅰ)因为时,, 代入关系式,得, 解得. 4分 (Ⅱ)由(Ⅰ)可知,套题每日的销售量, 所以每日销售套题所获得的利润 从而. 8分 令,得,且在上,,函数单调递增;在上,,函数单调递减, 所以是函数在内的极大值点,也是最大值点, 12分 所以当时,函数取得最大值. 故当销售价格为3.3元/套时,网校每日销售套题所获得的利润最大. 13分 21【解答】解:(1)f′(x)=lnx+x•=lnx+1, x=1时,f′(1)=1,f(1)=0, 故f(x)在x=1处的切线方程是:y=x﹣1, 联立, 消去y得:x2+(1﹣a)x+1=0, 由题意得:△=(1﹣a)2﹣4=0, 解得:a=3或﹣1; (2)由(1)得:f′(x)=lnx+1, x∈(0,)时,f′(x)<0,f(x)递减, x∈(,+∞)时,f′(x)>0,f(x)递增, ①0<t<t+≤,即0<t≤﹣时, f(x)min=f(t+)=(t+)ln(t+), ②0<t<<t+,即﹣<t<时, f(x)min=f()=﹣; ③≤t<t+,即t≥时,f(x)在递增, f(x)min=f(t)=tlnt; 综上,f(x)min=; (3)证明:设m(x)=﹣,(x∈(0,+∞)),则m′(x)=, x∈(0,1)时,m′(x)>0,m(x)递增, x∈(1,+∞)时,m′(x)<0,m(x)递减, 可得m(x)max=m(1)=﹣,当且仅当x=1时取到, 由(2)得f(x)=xlnx,(x∈(0,+∞))的最小值是﹣, 当且仅当x=时取到, 因此x∈(0,+∞)时,f(x)min≥﹣≥m(x)max恒成立, 又两次最值不能同时取到, 故对任意x∈(0,+∞),都有成立.查看更多