- 2021-04-13 发布 |
- 37.5 KB |
- 3页


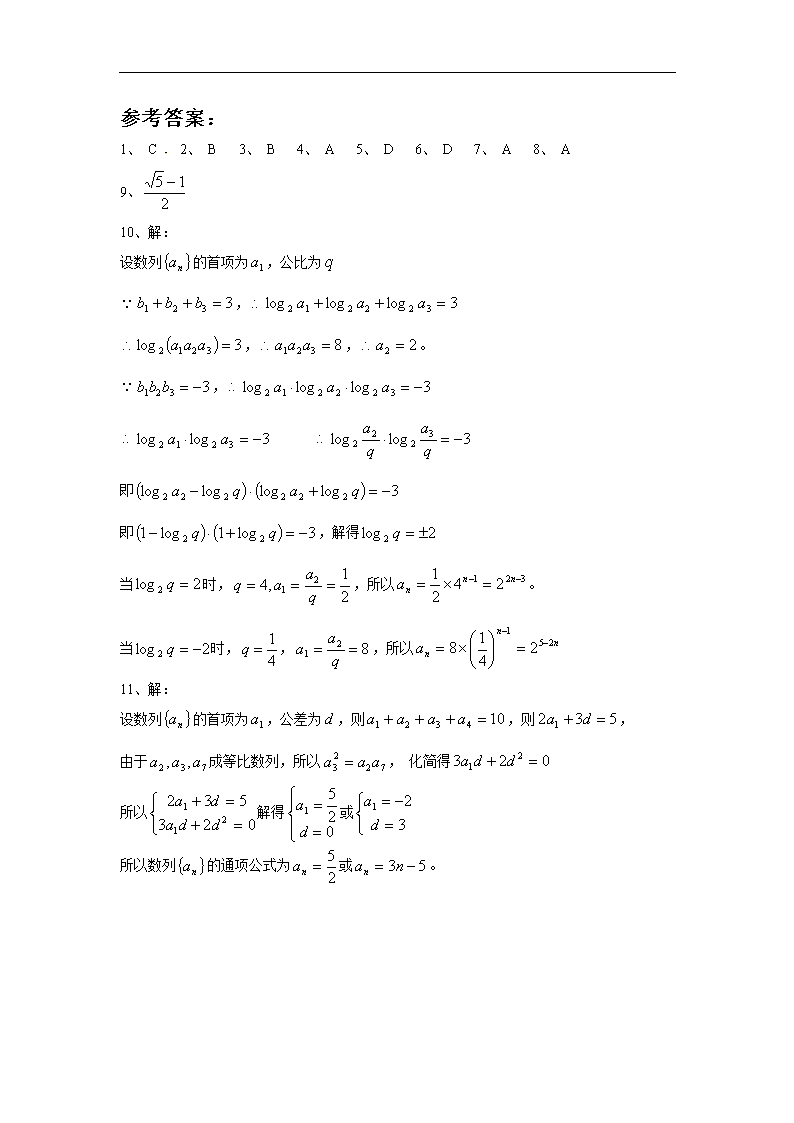
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学:2_4《等比数列的性质》作业
2. 4《等比数列的性质》作业 1、和的等比中项是 ( ) A. 1 B. C. D. 2 2、在3和9之间插入两个正数,使前3个数成等比数列,后3个数成等差数列,则这两个正数之和为 ( ) A. B. C. D. 3、在等比数列中,且,则的值为 ( ) A. 16 B. 27 C. 36 D. 81 4、已知公比为的等比数列,若,则数列是( ) A. 公比为的等比数列 B. 公比为的等比数列 C. 公差为的等差数列 D. 公差为的等差数列 5、在正项等比数列中,是方程的两个根, 则的值为 ( ) A. 32 B. 256 C. D. 64 6、若成等差数列,而和都分别成等比数列,则的值为( ) A.16 B.15 C.14 D.12 7、若正数组成等比数列,则一定是 ( ) A. 等差数列 B.既是等差数列有是等比数列 C. 等比数列 D. 既不是等差数列也不是等比数列 8、在等比数列中,已知,则= ( ) A. 8 B. -8 C. D. 16 9、若正项等比数列的公比为,且,成等差数列, 则 。 10、设是各项均为正数的等比数列,, 求。 11、已知等差数列的前4项和为10,且成等比数列, 求数列的通项公式。 参考答案: 1、 C 2、 B 3、 B 4、 A 5、 D 6、 D 7、 A 8、 A 9、 10、解: 设数列的首项为,公比为 , ,,。 , 即 即,解得 当时,,所以。 当时,,,所以 11、解: 设数列的首项为,公差为,则,则, 由于成等比数列,所以, 化简得 所以解得或 所以数列的通项公式为或。查看更多