山东省济宁邹城市第一中学2020届高三下学期第五次模拟考试数学试题

山东省济宁邹城市第一中学2020届高三下学期第五次模拟考试数学试题

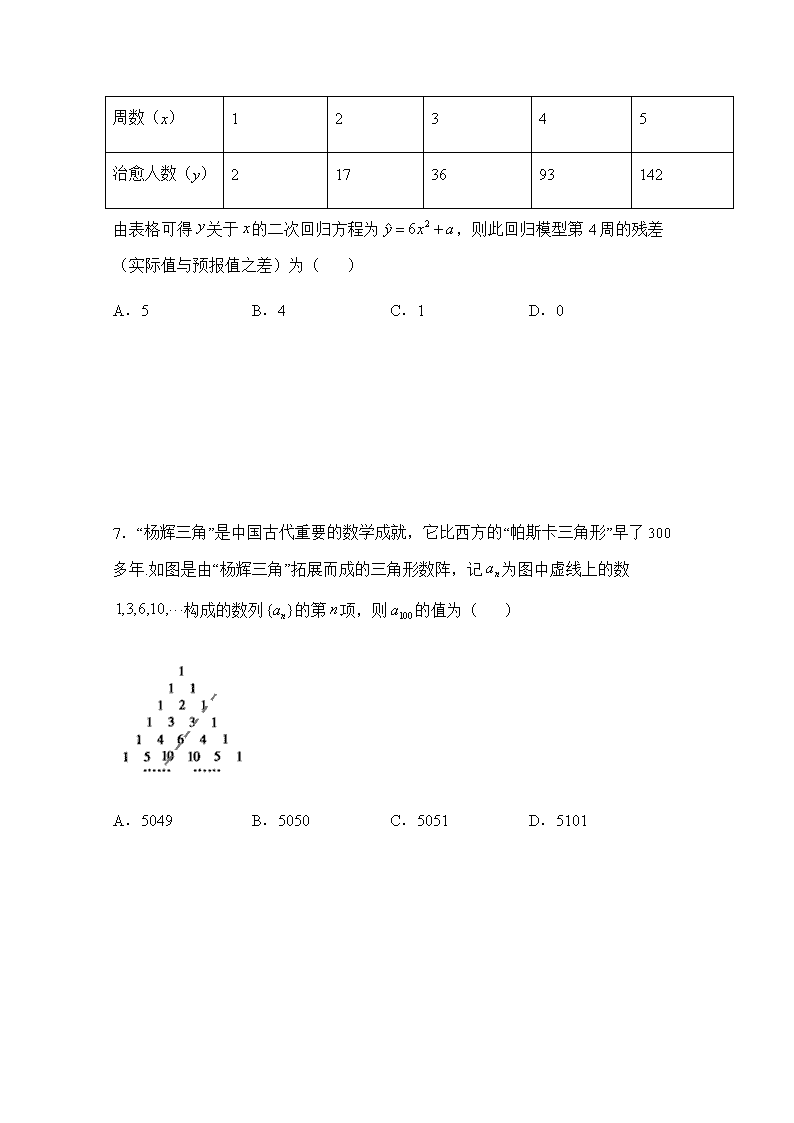
‎ 邹城一中2017级高三下学期第5次模拟考试 ‎ 数学试题 2020-6‎ 一、 单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知集合，，则（ ）‎ A． B． C． D．‎ ‎2．已知复数是正实数，则实数的值为( )‎ A． B． C． D．‎ ‎3．若圆与轴，轴均有公共点，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎4．抛物线的焦点是双曲线的一个焦点，则（ ）‎ A． B．8 C．4 D．1‎ ‎5.设p：实数满足，q：实数满足，则p是q的 ( ) ‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎6．2020年初，新型冠状病毒（）引起的肺炎疫情爆发以来，各地医疗机构采取了各种针对性的治疗方法，取得了不错的成效，某地开始使用中西医结合方法后，每周治愈的患者人数如下表所示：‎ 周数（x）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 治愈人数（y）‎ ‎2‎ ‎17‎ ‎36‎ ‎93‎ ‎142‎ 由表格可得关于的二次回归方程为，则此回归模型第4周的残差（实际值与预报值之差）为（ ）‎ A．5 B．4 C．1 D．0‎ ‎7．“杨辉三角”是中国古代重要的数学成就，它比西方的“帕斯卡三角形”早了多年.如图是由“杨辉三角”拓展而成的三角形数阵，记为图中虚线上的数构成的数列的第项，则的值为（ ）‎ A．5049 B．5050 C．5051 D．5101‎ 二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求的，全部选对得5分，选对但不全的得3分，有选错的得0分.‎ ‎9．下列命题中假命题是（ ）‎ A．若随机变量服从正态分布，，则；‎ B．已知直线平面，直线平面，则“”是“”的必要不充分条件；‎ C．若，则在方向上的正射影的数量为 D.‎ ‎10．已知向量，，，则下列结论正确的有（ ）‎ A． B．若∥，则 C．的最大值为2 D．的最大值为3‎ ‎11．如图，四棱锥中，平面底面，是等边三角形，底面是菱形，且，为棱的中点，为菱形的中心，下列结论正确的有（ ）‎ A．直线与平面平行 B．直线与直线垂直 C．线段与线段长度相等 D．与所成角的余弦值为 ‎12．已知函数，其中，，则下列选项中的条件使得仅有一个零点的有（ ）‎ A．为奇函数 B．‎ C．， D．，‎ 三、填空题:本大题共4小题，每小题5分，共20分.‎ ‎13．设常数，如果的二项展开式中项的系数为-80，那么______.‎ ‎14．已知函数，若对任意的实数，都存在唯一的实数，使，则实数的最大值是____．‎ ‎15．“学习强国”学习平台是由中宣部主管，以深入学习宣传习近平新时代中国特色社会主义思想为主要内容，立足全体党员、面向全社会的优质平台，现日益成为老百姓了解国家动态、紧跟时代脉搏的热门APP，该款软件主要设有“阅读文章”“视听学习”两个学习板块和“每日答题”“每周答题”“专项答题”“挑战答题”四个答题板块，某人在学习过程中，“阅读文章”与“视听学习”两大学习板块之间最多间隔一个答题板块的学习方法有______种. ‎ ‎16．三棱锥中，，且平面平面，则__________；若球与该三棱锥除以外的5条棱均相切，则球的半径为__________.(第一个空2分，第二个空3分)‎ 四、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.‎ ‎17．（本题满分10分）‎ 在中，角A，B，C对边分别为，，，且是与的等差中项. ‎ ‎（1）求角A； ‎ ‎（2）若，且的外接圆半径为1，求的面积.‎ ‎18．（本题满分12分）‎ 对于由正整数构成的数列，若对任意，“且，也是中的项，则称为数列”.设数列|满足，.‎ ‎（1）请给出一个的通项公式，使得既是等差数列也是“数列”，并说明理由；‎ ‎（2）根据你给出的通项公式，设的前项和为，求满足的正整数的最小值.‎ ‎19．（本题满分12分）‎ 如图,四棱锥中，，，，‎ ‎，．‎ （1） 求证：平面平面；‎ （2） 在线段上是否存在点，使得平面与平面所成锐二面角为？‎ 若存在，求的值；若不存在，说明理由．‎ ‎20．（本题满分12分）‎ 已知椭圆的离心率，直线与 相交于，两点，当时，‎ ‎（1）求椭圆的标准方程.‎ ‎（2）在椭圆上是否存在点，使得当时，的平分线总是平行于轴？若存在，求出点的坐标；若不存在，请说明理由.‎ 21． ‎（本题满分12分）‎ 为了提高生产线的运行效率，工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果，采集了生产线的技术改造前后各20次连续正常运行的时间长度（单位：天）数据，并绘制了如下茎叶图：‎ ‎（1）①设所采集的40个连续正常运行时间的中位数，并将连续正常运行时间超过和不超过的次数填入下面的22列联表：‎ 超过 不超过 改造前 改造后 试写出，，，的值；‎ ‎②根据（1）中的22列联表，能否有的把握认为生产线技术改造前后的连续正常运行时间有差异？‎ 附：，‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎（2）工厂的生产线的运行需要进行维护.工厂对生产线的生产维护费用包括正常维护费、保障维护费两种,对生产线设定维护周期为天（即从开工运行到第天（）进行维护.生产线在一个生产周期内设置几个维护周期，每个维护周期相互独立.在一个维护周期内，若生产线能连续运行，则不会产生保障维护费；若生产线不能连续运行，则产生保障维护费.经测算，正常维护费为0.5万元次；保障维护费第一次为0.2万元周期，此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期（以120天计）内的维护方案：，，2，3，4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率，求一个生产周期内生产维护费的分布列及期望值.‎ 邹城一中2017级高三下学期第5次模拟考试答案 一、单选DCAB AABA 二、多选BCD AC ABD BD 三、填空 13. -2 14. 15. 432 16. ； ‎ 四、解答 ‎17（1）因为是与的等差中项.‎ 所以.‎ 由正弦定理得，从而可得，‎ 又为三角形的内角，所以，于是，又为三角形内角，因此.‎ ‎（2）设的外接圆半径为，则，，‎ 由余弦定理得，‎ 即，所以.‎ 所以的面积为.‎ ‎18.（1）给出的通项公式为.‎ 因为对任意，，所以是公差为2的等差数列.‎ 对任意，且，，‎ 所以是“数列”.‎ ‎（2）因为是等差数列，所以.‎ 因为单调递增，且，，‎ 所以的最小值为8.‎ 注：以下答案也正确，解答步骤参考上面内容：‎ ‎①，，的最小值为7；‎ ‎②，，的最小值为6.‎ ‎19（1）证明：因为四边形为直角梯形，‎ 且, ,,所以， ‎ 又因为．根据余弦定理得 ‎ 所以，故. ‎ 又因为, ,且,平面，所以平面， ‎ 又因为平面PBC，所以 ‎（2）由（1）得平面平面, 设为的中点，连结 ，因为,‎ 所以,,又平面平面，平面平面，‎ 平面.‎ 如图，以为原点分别以，和垂直平面的方向为轴正方向，建立空间直角坐标系，‎ 则，，，，， ‎ 假设存在满足要求，设，即，‎ 所以,易得平面的一个法向量为. ‎ 设为平面的一个法向量，， ‎ 由得，不妨取.‎ 因为平面与平面所成的锐二面角为，所以，‎ 解得，（不合题意舍去）.故存在点满足条件，且.‎ ‎20（1）设椭圆的半焦距为因为离心率，所以，‎ 由解得.不妨设，，则.‎ 所以，从而，.‎ 所以椭圆的标准方程为.‎ ‎（2）假设存在点，设，.‎ 由，消去得.‎ 因为，所以，‎ 且，.‎ 由的平分线平行于轴，得 所以，即，‎ 可得，‎ 所以，‎ 整理得.‎ 当变化时，上式恒成立，‎ 所以，解得或.‎ 故满足条件的点的坐标为或.经检验这两点都不符合，故不存在P不符合条件 ‎21（1）由茎叶图知，根据茎叶图可得：，，，.‎ ‎（2）由于，所以有的把握认为连续正常运行时间有差异.‎ ‎（Ⅱ）生产周期内有4个维护周期，一个维护周期为30天，一个维护周期内，生产线需保障维护的概率为.‎ 设一个生产周期内需保障维护的次数为次，则正常维护费为万元，保障维护费为万元.‎ 故一个生产周期内需保障维护次时的生产维护费为万元.‎ 由于，设一个生产周期内的生产维护费为万元，则分布列为 ‎2‎ ‎2.2‎ ‎2.6‎ ‎3.2‎ ‎4‎ 则万元.‎ 故一个生产周期内生产维护费的期望值为2.275万元.‎