2018-2019学年广东省清远市高一上学期期末考试数学试题（解析版）

2018-2019学年广东省清远市高一上学期期末考试数学试题（解析版）

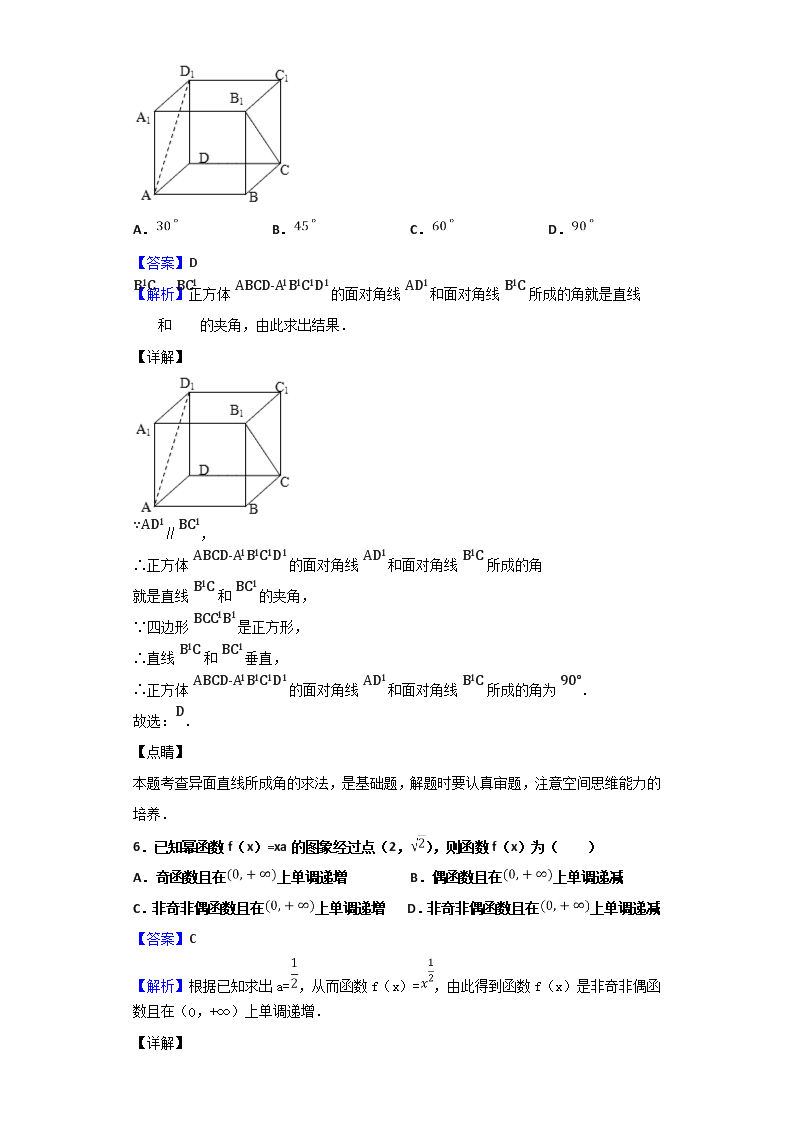
‎2018-2019学年广东省清远市高一上学期期末考试数学试题 一、单选题 ‎1．如图所示的韦恩图中，若A={1，2，3，4，5}，B={3，4，5，6，7}，则阴影部分表示的集合是（　　）‎ A．2，3，4，5，6， B．2，3，4，‎ C．4，5，6， D．2，6，‎ ‎【答案】D ‎【解析】根据图象确定阴影部分的集合元素特点，利用集合的交集和并集进行求解即可．‎ ‎【详解】‎ 阴影部分对应的集合为{x|x∈A∪B且x∉A∩B}， ‎ ‎∵A∪B={1，2，3，4，5，6，7}，A∩B={3，4，5}， ‎ ‎∴阴影部分的集合为{1，2，6，7}， ‎ 故选：D．‎ ‎【点睛】‎ 本题主要考查集合的运算，根据Venn图表示集合关系是解决本题的关键．‎ ‎2．若a＞b，则下列各式正确的是（　　）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】由不等式的基本性质，逐一检验即可．‎ ‎【详解】‎ 因为a＞b，所以a-2＞b-2，故选项A正确，‎ ‎2-a＜2-b，故选项B错误， ‎ ‎-2a＞-2b，故选项C错误， ‎ a2，b2无法比较大小，故选项D错误， ‎ 故选：A．‎ ‎【点睛】‎ 本题考查了不等式的基本性质，意在考查学生对该知识的理解掌握水平.‎ ‎3．下列函数中，能用二分法求零点的是（　　）‎ A． B．‎ C． D．‎ ‎【答案】D ‎【解析】利用零点判定定理以及函数的图象，判断选项即可．‎ ‎【详解】‎ 由题意以及零点判定定理可知：只有选项D能够应用二分法求解函数的零点，‎ 故选：D．‎ ‎【点睛】‎ 本题考查了零点判定定理的应用和二分法求解函数的零点，是基本知识的考查．‎ ‎4．下列选项中，两个函数表示同一个函数的是（　　）‎ A．， B．，‎ C．， D．，‎ ‎【答案】C ‎【解析】根据函数的定义域，即可判断选项A的两个函数不是同一个函数，根据函数解析式不同，即可判断选项B，D的两函数都不是同一个函数，从而为同一个函数的只能选C．‎ ‎【详解】‎ A.的定义域为{x|x≠0}，y=1的定义域为R，定义域不同，不是同一个函数； B.和y=|x|的解析式不同，不是同一函数； C．y=x的定义域为R，y=lnex=x的定义域为R，定义域和解析式都相同，是同一个函数； D.=|x-1|,=x-1,解析式不同，不是同一个函数． 故选：C．‎ ‎【点睛】‎ 本题考查同一函数的定义，判断两函数是否为同一个函数的方法：看定义域和解析式是否都相同．‎ ‎5．在正方体ABCD-A1B1C1D1中，异面直线AD1和B1C所成的角是（　　）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】正方体ABCD-A1B1C1D1的面对角线AD1和面对角线B1C所成的角就是直线B1C和BC1的夹角，由此求出结果．‎ ‎【详解】‎ ‎∵AD1∥BC1，‎ ‎∴正方体ABCD-A1B1C1D1的面对角线AD1和面对角线B1C所成的角 就是直线B1C和BC1的夹角，‎ ‎∵四边形BCC1B1是正方形，‎ ‎∴直线B1C和BC1垂直，‎ ‎∴正方体ABCD-A1B1C1D1的面对角线AD1和面对角线B1C所成的角为90°．‎ 故选：D．‎ ‎【点睛】‎ 本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．‎ ‎6．已知幂函数f（x）=xa的图象经过点（2，），则函数f（x）为（　　）‎ A．奇函数且在上单调递增 B．偶函数且在上单调递减 C．非奇非偶函数且在上单调递增 D．非奇非偶函数且在上单调递减 ‎【答案】C ‎【解析】根据已知求出a=，从而函数f（x）=，由此得到函数f（x）是非奇非偶函数且在（0，+∞）上单调递增．‎ ‎【详解】‎ ‎∵幂函数f（x）=xa的图象经过点（2，）， ∴2a=，解得a=， ∴函数f（x）=， ∴函数f（x）是非奇非偶函数且在（0，+∞）上单调递增． 故选：C．‎ ‎【点睛】‎ 本题考查命题真假的判断，考查幂函数的性质等基础知识，考查运算求解能力，是基础题．‎ ‎7．已知函数f（x）=，若f（f（-1））=6，则实数a的值为（　　）‎ A．1 B． C．2 D．4‎ ‎【答案】A ‎【解析】利用分段函数的解析式，由里及外逐步求解函数值得到方程求解即可．‎ ‎【详解】‎ 函数f（x）=，若f（f（-1））=6， 可得f（-1）=4，f（f（-1））=f（4）=4a+log24=6， 解得a=1． 故选：A．‎ ‎【点睛】‎ 本题考查分段函数的应用，函数值的求法，考查计算能力．‎ ‎8．函数y=1g（1-x）+的定义域是（　　）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】可看出，要使得原函数有意义，则需满足解出x的范围即可．‎ ‎【详解】‎ 要使原函数有意义，则： 解得-1≤x＜1； ∴原函数的定义域是[-1，1）． 故选：B．‎ ‎【点睛】‎ 本题主要考查函数定义域的概念及求法，考查对数函数的定义域和一元二次不等式的解法．意在考查学生对这些知识的理解掌握水平.‎ ‎9．在如图所示的多面体ABCDB1C1D1中，四边形ABCD、四边形BCC1B1、四边形CDC1C1都是边长为6的正方形，则此多面体ABCDB1C1D1的体积（　　）‎ A．72 B．144 C．180 D．216‎ ‎【答案】B ‎【解析】把该几何体补成正方体ABCD-A1B1C1D1，此多面体ABCDB1C1D1的体积V=-，求之即可．‎ ‎【详解】‎ 如图，把该几何体补成正方体ABCD-A1B1C1D1， 此多面体ABCDB1C1D1的体积V=-=63-=144． 故选：B．‎ ‎【点睛】‎ 本题主要考查四棱锥体积的求法，考查化归与转化思想、数形结合思想，是中档题．‎ ‎10．函数f（x）=|x3|•ln的图象大致为（　　）‎ A． B．‎ C． D．‎ ‎【答案】A ‎【解析】判断函数的奇偶性和对称性，利用特殊点的函数值是否对应进行排除即可．‎ ‎【详解】‎ f（-x）=|x3|•ln=-|x3|•ln=-f（x），则函数f（x）是奇函数，图象关于原点对称，排除B，D， f（）=ln=ln＜0，排除C， 故选：A．‎ ‎【点睛】‎ 本题主要考查函数图象的识别和判断，利用函数奇偶性和特殊值进行排除是解决本题的关键．‎ ‎11．设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：‎ ‎①若m⊥α，n∥α，则m⊥n ‎②若α⊥γ，β⊥γ，则α∥β ‎③若α⊥β，m⊂α，则m⊥β ‎④若α∥β，β∥γ，m⊥α，则m⊥γ 其中正确命题的序号是（　　）‎ A．和 B．和 C．和 D．和 ‎【答案】B ‎【解析】根据空间直线和平面平行、垂直的性质分别进行判断即可．‎ ‎【详解】‎ ‎①若m⊥α，n∥α，则m⊥n成立，故①正确，‎ ‎②若α⊥γ，β⊥γ，则α∥β不成立，两个平面没有关系，故②错误 ‎ ‎③若α⊥β，m⊂α，则m⊥β不成立，可能m与β相交，故③错误， ‎ ‎④若α∥β，β∥γ，m⊥α，则m⊥γ，成立，故④正确， ‎ 故正确的是①④， ‎ 故选：B．‎ ‎【点睛】‎ 本题主要考查命题的真假判断，涉及空间直线和平面平行和垂直的判定和性质，考查学生的空间想象能力．‎ ‎12．若函数y=f（x）图象上存在不同的两点A，B关于y轴对称，则称点对[A，B]是函数y=f（x）的一对“黄金点对”（注：点对[A，B]与[B，A]可看作同一对“黄金点对”）．已知函数f（x）=，则此函数的“黄金点对“有（　　）‎ A．0对 B．1对 C．2对 D．3对 ‎【答案】D ‎【解析】根据“黄金点对“，只需要先求出当x＜0时函数f（x）关于y轴对称的函数的解析式，再作出函数的图象，利用两个图象交点个数进行求解即可．‎ ‎【详解】‎ 由题意知函数f（x）=2x，x＜0关于y轴对称的函数为，x＞0，‎ 作出函数f（x）和，x＞0的图象，‎ 由图象知当x＞0时，f（x）和y=（）x，x＞0的图象有3个交点．‎ 所以函数f（x）的““黄金点对“有3对．‎ 故选：D．‎ ‎【点睛】‎ 本题主要考查分段函数的应用，结合“黄金点对“的定义，求出当x＜0时函数f（x）关于y轴对称的函数的解析式，作出函数的图象，利用数形结合是解决本题的关键．‎ 二、填空题 ‎13．若，，则a、b的大小关系是______．（用“＜”连接）‎ ‎【答案】‎ ‎【解析】容易看出，＜0，＞0，从而可得出a，b的大小关系．‎ ‎【详解】‎ ‎ ，＞0，,∴a＜b． 故答案为：a＜b．‎ ‎【点睛】‎ 本题主要考查对数函数的单调性，考查对数函数和指数函数的值域．意在考查学生对这些知识的理解掌握水平和分析推理能力.‎ ‎14．一个几何体的三视图如图所示，其中正视图与侧视图都是斜边长为4的直角三角形，俯视图是半径为2的四分之一圆周和两条半径，则这个几何体的体积为______．‎ ‎【答案】‎ ‎【解析】由题得几何体为圆锥的，根据三视图的数据计算体积即可．‎ ‎【详解】‎ 由三视图可知几何体为圆锥的，圆锥的底面半径为1，母线长为2， ∴圆锥的高为． ∴V=×π×12×=． 故答案为：．‎ ‎【点睛】‎ 本题主要考查了圆锥的三视图和体积计算，属于基础题．‎ ‎15．直三棱柱ABC-A1B1C1，内接于球O，且AB⊥BC，AB=3．BC=4．AA1=4，则球O的表面积______．‎ ‎【答案】‎ ‎【解析】利用三线垂直联想长方体，而长方体外接球直径为其体对角线长，容易得到球半径，得解．‎ ‎【详解】‎ 直三棱柱中，易知AB，BC，BB1两两垂直， 可知其为长方体的一部分， 利用长方体外接球直径为其体对角线长， 可知其直径为， ∴=41π， 故答案为：41π．‎ ‎【点睛】‎ 本题主要考查了三棱柱的外接球和球的表面积的计算，意在考查学生对这些知识的理解掌握水平和空间想象能力.‎ ‎16．已知偶函数，x∈R，满足f（1-x）=f（1+x），且当0＜x＜1时，f（x）=ln（x+），e为自然数，则当2＜x＜3时，函数f（x）的解析式为______．‎ ‎【答案】‎ ‎【解析】由f（1-x）=f（1+x），再由偶函数性质得到函数周期，再求当2＜x＜3时f（x）解析式．‎ ‎【详解】‎ 因为f（x）是偶函数，满足f（1-x）=f（1+x），所以f（1+x）=f（x-1），所以f（x）周期是2．‎ 当2＜x＜3时，0＜x-2＜1，‎ 所以f（x-2）=ln（x-2+）=f（x），‎ 所以函数f（x）的解析式为f（x）=ln（x-2+）．‎ 故答案为：f（x）=ln（x-2+）．‎ ‎【点睛】‎ 本题主要考查函数的奇偶性，考查利用函数的周期性求解析式，意在考查学生对这些知识的理解掌握水平和分析推理能力.‎ 三、解答题 ‎17．化简或求下列各式的值．‎ ‎（1）；‎ ‎（2）（lg5）2+lg5•lg20+．‎ ‎【答案】（1）；（2）2‎ ‎【解析】（1）进行分数指数幂的运算即可； （2）进行对数的运算即可．‎ ‎【详解】‎ ‎（1）原式=；‎ ‎（2）原式=lg5（lg5+lg20）+lg4=2（lg5+lg2）=2．‎ ‎【点睛】‎ 本题主要考查分数指数幂和对数的运算，考查对数的换底公式．意在考查学生对这些知识的理解掌握水平和计算能力.‎ ‎18．已知集合A={x|x2-7x+6＜0}，B={x|4-t＜x＜t}，R为实数集．‎ ‎（1）当t=4时，求A∪B及A∩∁RB；‎ ‎（2）若A∪B=A，求实数t的取值范围．‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】（1）由二次不等式的解法得：，由集合的交、并、补的运算得，，所以，，（2）由集合间的包含关系得：因为，得：，讨论①，②时，运算即可得解.‎ ‎【详解】‎ ‎（1）解二次不等式x2-7x+6＜0得：1＜x＜6，即A=(1,6)， 当t=4时，B=(0,4)，CRB=， 所以A∪B=(0,6)，A∩CRB=[4,6)， 故答案为：A∪B=(0,6)，A∩CRB=[4,6)，‎ ‎（2）由A∪B=A，得：B ⊆ A， ‎ ‎①当4-t≥t即t≤2时，B=，满足题意， ②B≠时， 由B⊆A得：， 解得：2＜t≤3， 综合①②得： 实数t的取值范围为：t≤3， 故答案为：t≤3．‎ ‎【点睛】‎ 本题考查了二次不等式的解法、集合的交、并、补的运算及集合间的包含关系，属简单题．‎ ‎19．在长方体ABCD-A1B1C1D1中，求证：‎ ‎（1）AB∥平面A1B1C；‎ ‎（2）平面ABB1A1⊥平面A1BC．‎ ‎【答案】（1）见解析；（2）见解析 ‎【解析】（1）推导出AB∥A1B1，由此能证明AB∥平面A1B1C． （2）推导出BC⊥AB，BC⊥BB1，从而BC⊥平面ABB1A1，由此能证明平面ABB1A1⊥平面A1BC．‎ ‎【详解】‎ 证明：（1）在长方体ABCD-A1B1C1D1中，‎ ‎∵AB∥A1B1，且AB⊄平面A1B1C，A1B1⊂平面A1B1C，‎ ‎∴AB∥平面A1B1C．‎ ‎（2）在长方体ABCD-A1B1C1D1中，‎ ‎∵BC⊥AB，BC⊥BB1，AB∩BB1=B，‎ ‎∴BC⊥平面ABB1A1，‎ ‎∵BC⊂平面A1BC，∴平面ABB1A1⊥平面A1BC．‎ ‎【点睛】‎ 本题考查线面平行、面面垂直的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查化归与转化思想，是中档题．‎ ‎20．已知函数f（x）=-，若x∈R，f（x）满足f（-x）=-f（x）．‎ ‎（1）求实数a的值；‎ ‎（2）判断函数f（x）（x∈R）的单调性，并说明理由；‎ ‎（3）若对任意的t∈R，不等式f（t2-4t）+f（-k）＜0恒成立，求k的取值范围．‎ ‎【答案】（1）1；（2）‎ ‎【解析】（1）根据f（-x）=-f（x）代入求得a的值； （2）f（x）是定义域R上的单调减函数，利用定义证明即可； （3）根据题意把不等式化为t2-4t＞k，求出f（t）=t2-4t的最小值，即可得出k的取值范围．‎ ‎【详解】‎ ‎（Ⅰ）函数f（x）=-，x∈R，且f（-x）=-f（x）， ∴-=-+， ‎ ‎∴a=+=+=1； （Ⅱ）f（x）=-是定义域R上的单调减函数，证明如下： 任取x1、x2∈R，且x1＜x2， 则f（x1）-f（x2）=（-）-（-）=-=， 由（+1）（+1）＞0，当x1＜x2时，＜， ∴-＞0，∴f（x1）＞f（x2）， ∴f（x）是定义域R上的单调减函数； （Ⅲ）对任意的t∈R，不等式f（t2-4t）+f（-k）＜0恒成立， 则f（t2-4t）＜-f（-k）=f（k）， 根据f（x）是定义域R上的单调减函数，得t2-4t＞k， 设f（t）=t2-4t，t∈R，则f（t）=（t-2）2-4≥-4， ∴k的取值范围是k＜-4．‎ ‎【点睛】‎ 本题考查了函数的奇偶性与单调性应用问题，也考查了不等式恒成立问题，是中档题．‎ ‎21．如图所示，已知长方形ABCD，AD=2CD=4，M、N分别为AD、BC的中点，将长方形ABCD沿MN折到MNFE位置，且使平面MNFE⊥平面ABCD．‎ ‎（1）求证：直线CM⊥面DFN；‎ ‎（2）求点C到平面FDM的距离．‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ ‎（1）推导出DN⊥CM，CM⊥FN，由此能证明CM⊥平面DFN．（2）以M为原点，MN为x轴，MA为y轴，ME为z轴，建立空间直角坐标系，利用向量法能求出点C到平面FDM的距离．‎ ‎【详解】‎ 证明：（1）∵长方形ABCD，AD=2CD=4，M、N分别为AD、BC的中点， 将长方形ABCD沿MN折到MNFE位置，且使平面MNFE⊥平面ABCD． ∴DN⊥CM，CM⊥FN，‎ 又DN∩FN=N，∴CM⊥平面DFN．‎ ‎ 解：（2）以M为原点，MN为x轴，MA为y轴，ME为z轴，建立空间直角坐标系， 则C（2，-2，0），D（0，-2，0），F（2，0，2），M（0，0，0）， =（2，-2，0），=（0，-2，0），=（2，0，2）， 设平面FDM的法向量=（x，y，z）， 则，取x=1，得=（1，0，-1）， ∴点C到平面FDM的距离d===．‎ ‎【点睛】‎ 本题考查线面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题．‎ ‎22．已知函数f（x）=ax2-4ax+1+b（a＞0）的定义域为[2，3]，值域为[1，4]；设g（x）=．‎ ‎（1）求a，b的值；‎ ‎（2）若不等式g（2x）-k•2x≥0在x∈[1，2]上恒成立，求实数k的取值范围．‎ ‎【答案】（1）；（2）‎ ‎【解析】（1）根据函数f（x）=ax2‎ ‎-4ax+1+b（a＞0）的定义域为[2，3]，值域为[1，4]，其图象对称轴为直线x=2，且g（x）的最小值为1，最大值为4，列出方程可得实数a，b的值； （2）若不等式g（2x）-k•2x≥0在x∈[1，2]上恒成立，分离变量k，在x∈[1，2]上恒成立，进而得到实数k的取值范围．‎ ‎【详解】‎ ‎(1）∵函数f（x）=ax2-4ax+1+b（a＞0）其图象对称轴为直线x=2， 函数的定义域为[2，3]，值域为[1，4]， ∴， 解得：a=3，b=12； （2）由（Ⅰ）得：f（x）=3x2-12x+13，g（x）==． 若不等式g（2x）-k•2x≥0在x∈[1，2]上恒成立， 则k≤（）2-2（）+1在x∈[1，2]上恒成立， 2x∈[2，4]，∈[，]，当=，即x=1时，（）2-2（）+1取最小值， 故k≤．‎ ‎【点睛】‎ 本题考查二次函数在闭区间上的最值，考查函数恒成立问题问题，考查数形结合与等价转化、函数与方程思想的综合应用，是中档题．‎