- 2021-04-13 发布 |
- 37.5 KB |
- 16页


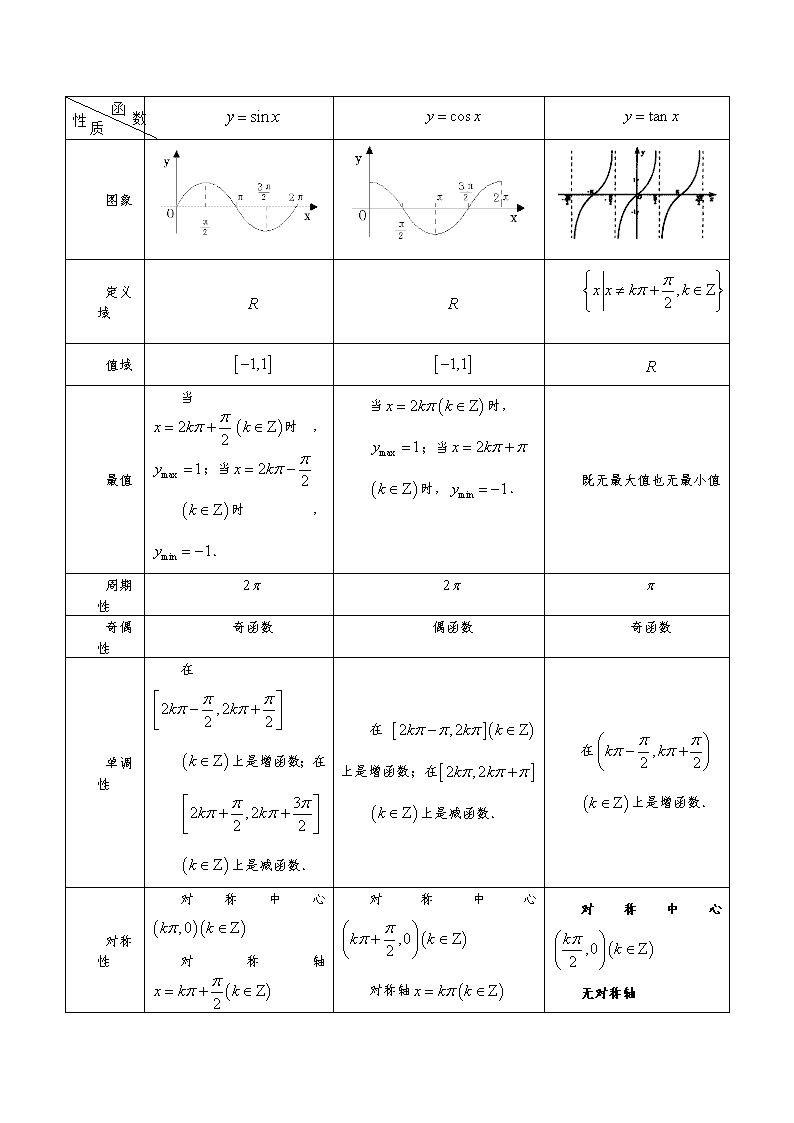
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江高考数学三角函数最实用知识点汇编
P v x y A O M T 高中数学必修 4 知识点总结 第一章 三角函数 2、角 的顶点与原点重合,角的始边与 轴的非负半轴重合,终边落在第几象限,则称 为第几象限 角. 第一象限角的集合为 第二象限角的集合为 第三象限角的集合为 第四象限角的集合为__________________ 终边在 轴上的角的集合为 终边在 轴上的角的集合为 终边在坐标轴上的角的集合为 3、与角 终边相同的角的集合为 4、长度等于半径长的弧所对的圆心角叫做 弧度. 5、半径为 的圆的圆心角 所对弧的长为 ,则角 的弧度数的绝对值是 . 6、弧度制与角度制的换算公式: , , . 7、若扇形的圆心角为 ,半径为 ,弧长为 ,周长为 ,面积为 ,则 , , . 8 、 设 是 一 个 任 意 大 小 的 角 , 的 终 边 上 任 意 一 点 的 坐 标 是 , 它 与 原 点 的 距 离 是 ,则 , , . 9、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正, 第三象限正切为正,第四象限余弦为正. 10、三角函数线: , , . 11 、 角 三 角 函 数 的 基 本 关 系 : 正角: 按逆时针方向旋转形成的角 1、任意角 负角: 按顺时针方向旋转形成的角 零角: 不作任何旋转形成的角 α x α { }360 360 90 ,k k kα α⋅ < < ⋅ + ∈Ζ { }360 180 360 270 ,k k kα α⋅ + < < ⋅ + ∈Ζ x { }180 ,k kα α = ⋅ ∈Ζ y { }180 90 ,k kα α = ⋅ + ∈Ζ { }90 ,k kα α = ⋅ ∈Ζ α { }360 ,k kβ β α= ⋅ + ∈Ζ 1 r α l α l r α = 2 360π = 1 180 π= 1801 57.3π = ≈ ( )α α为弧度制 r l C S l r α= 2C r l= + 21 1 2 2S lr rα= = α α Ρ ( ),x y ( )2 2 0r r x y= + > sin y r α = cos x r α = ( )tan 0y xx α = ≠ sinα = ΜΡ cosα = ΟΜ tanα = ΑΤ ( ) 2 21 sin cos 1α α+ = ; . 三角函数的诱导公式: , , . , , . , , . , , . 口诀:鸡便偶不变,符号看象限. , . , . 口诀:鸡便偶不变,符号看象限. 13、①的图象上所有点向左(右)平移 个单位长度,得到函数 的图象;再将函数 的 图 象 上 所 有 点 的 横 坐 标 伸 长 ( 缩 短 ) 到 原 来 的 倍 ( 纵 坐 标 不 变 ),得 到 函 数 的图象;再将函数 的图象上所有点的纵坐标伸长(缩短)到原来的 倍 (横坐标不变),得到函数 的图象. ②数 的图象上所有点的横坐标伸长(缩短)到原来的 倍(纵坐标不变),得到函数 的图象;再将函数 的图象上所有点向左(右)平移 个单位长度,得到函数 的图象;再将函数 的图象上所有点的纵坐标伸长(缩短)到原来的 倍 (横坐标不变),得到函数 的图象. 14、函数 的性质: ①振幅: ;②周期: ;③频率: ;④相位: ;⑤初相: . 函数 ,当 时,取得最小值为 ;当 时,取得最大值为 ,则 , , . 15、正弦函数、余弦函数和正切函数的图象与性质: ( )2 2 2 2sin 1 cos ,cos 1 sinα α α α= − = − ( ) sin2 tancos α αα = sinsin tan cos ,cos tan αα α α α α = = ( ) ( )1 sin 2 sinkπ α α+ = ( )cos 2 coskπ α α+ = ( ) ( )tan 2 tank kπ α α+ = ∈Ζ ( ) ( )2 sin sinπ α α+ = − ( )cos cosπ α α+ = − ( )tan tanπ α α+ = ( ) ( )3 sin sinα α− = − ( )cos cosα α− = ( )tan tanα α− = − ( ) ( )4 sin sinπ α α− = ( )cos cosπ α α− = − ( )tan tanπ α α− = − ( )5 sin cos2 π α α − = cos sin2 π α α − = ( )6 sin cos2 π α α + = cos sin2 π α α + = − ϕ ( )siny x ϕ= + ( )siny x ϕ= + 1 ω ( )siny xω ϕ= + ( )siny xω ϕ= + Α ( )siny xω ϕ= Α + siny x= 1 ω siny xω= siny xω= ϕ ω ( )siny xω ϕ= + ( )siny xω ϕ= + Α ( )siny xω ϕ= Α + ( )( )sin 0, 0y xω ϕ ω= Α + Α > > Α 2π ωΤ = 1 2f ω π= =Τ xω ϕ+ ϕ ( )siny xω ϕ= Α + + Β 1x x= miny 2x x= maxy ( )max min 1 2 y yΑ = − ( )max min 1 2 y yΒ = + ( )2 1 1 22 x x x x Τ = − < 图象 定义 域 值域 最值 当 时 , ; 当 时 , . 当 时, ;当 时, . 既无最大值也无最小值 周期 性 奇偶 性 奇函数 偶函数 奇函数 单调 性 在 上是增函数;在 上是减函数. 在 上是增函数;在 上是减函数. 在 上是增函数. 对称 性 对 称 中 心 对 称 轴 对 称 中 心 对 称 中 心 无对称轴 siny x= cosy x= tany x= R R ,2x x k k ππ ≠ + ∈Ζ [ ]1,1− [ ]1,1− R 2 2x k ππ= + ( )k ∈Ζ max 1y = 2 2x k ππ= − ( )k ∈Ζ min 1y = − ( )2x k kπ= ∈Ζ max 1y = 2x kπ π= + ( )k ∈Ζ min 1y = − 2π 2π π 2 ,22 2k k π ππ π − + ( )k ∈Ζ 32 ,22 2k k π ππ π + + ( )k ∈Ζ [ ]( )2 ,2k k kπ π π− ∈Ζ [ ]2 ,2k kπ π π+ ( )k ∈Ζ ,2 2k k π ππ π − + ( )k ∈Ζ ( )( ),0k kπ ∈Ζ ( ),02k k ππ + ∈Ζ ( ),02 k k π ∈Ζ 函 数性 质 对称轴 第二章 平面向量 16、向量:既有大小,又有方向的量. 数量:只有大小,没有方向的量. 有向线段的三要素:起点、方向、长度. 零向量:长度为 的向量. 单位向量:长度等于 个单位的向量. 平行向量(共线向量):方向相同或相反的非零向量.零向量与任一向量平行. 相等向量:长度相等且方向相同的向量. 17、向量加法运算: ⑴三角形法则的特点:首尾相连. ⑵平行四边形法则的特点:共起点. ⑶ 三 角 形 不 等 式 : . ⑷运算性质:①交换律: ; ②结合律: ;③ . ⑸ 坐 标 运 算 : 设 , , 则 . 18、向量减法运算: ⑴三角形法则的特点:共起点,连终点,方向指向被减向量. ⑵ 坐 标 运 算 : 设 , , 则 . 设 、 两点的坐标分别为 , ,则 . 19、向量数乘运算: ⑴实数 与向量 的积是一个向量的运算叫做向量的数乘,记作 . ① ; ② 当 时 , 的 方 向 与 的 方 向 相 同;当 时 , 的 方 向 与 的 方 向 相 反;当 时 , . ⑵运算律:① ;② ;③ . ⑶坐标运算:设 ,则 . ( ) 2x k k ππ= + ∈Ζ ( )x k kπ= ∈Ζ 0 1 a b a b a b− ≤ + ≤ + a b b a+ = + ( ) ( )a b c a b c+ + = + + 0 0a a a+ = + = ( )1 1,a x y= ( )2 2,b x y= ( )1 2 1 2,a b x x y y+ = + + ( )1 1,a x y= ( )2 2,b x y= ( )1 2 1 2,a b x x y y− = − − Α Β ( )1 1,x y ( )2 2,x y ( )1 2 1 2,x x y yΑΒ = − − λ a aλ a aλ λ= 0λ > aλ a 0λ < aλ a 0λ = 0aλ = ( ) ( )a aλ µ λµ= ( )a a aλ µ λ µ+ = + ( )a b a bλ λ λ+ = + ( ),a x y= ( ) ( ), ,a x y x yλ λ λ λ= = b a C Β Α a b C C− = Α − ΑΒ = Β 20、向量共线定理:向量 与 共线,当且仅当有唯一一个实数 ,使 . 设 , ,其中 ,则当且仅当 时,向量 、 共线. 21、平面向量基本定理:如果 、 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量 , 有且只有一对实数 、 ,使 .(不共线的向量 、 作为这一平面内所有向量的一组基 底) 22 、定比分点坐标公式:设点 是线段 上的一点, 、 的坐标分别是 , ,当 时,点 的坐标是 .(当 23、平面向量的数量积: ⑴ .零向量与任一向量的数量积为 . ⑵性质:设 和 都是非零向量,则① .②当 与 同向时, ;当 与 反 向时, ; 或 .③ . ⑶运算律:① ;② ;③ . ⑷坐标运算:设两个非零向量 , ,则 . 若 , 则 , 或 . 设 , , 则 . 设 、 都 是 非 零 向 量 , , , 是 与 的 夹 角 , 则 . 第三章 三角恒等变换 24、两角和与差的正弦、余弦和正切公式: ⑴ ;⑵ ; ⑶ ;⑷ ; ⑸ ( ); ( )0a a ≠ b λ b aλ= ( )1 1,a x y= ( )2 2,b x y= 0b ≠ 1 2 2 1 0x y x y− = a ( )0b b ≠ 1e 2e a 1 λ 2 λ 1 1 2 2a e eλ λ= + 1e 2e Ρ 1 2 Ρ Ρ 1 Ρ 2 Ρ ( )1 1,x y ( )2 2,x y 1 2 λΡ Ρ = ΡΡ Ρ 1 2 1 2,1 1 x x y yλ λ λ λ + + + + 时,就为中点公式。)1=λ ( )cos 0, 0,0 180a b a b a bθ θ⋅ = ≠ ≠ ≤ ≤ 0 a b 0a b a b⊥ ⇔ ⋅ = a b a b a b⋅ = a b a b a b⋅ = − 22a a a a⋅ = = a a a= ⋅ a b a b⋅ ≤ a b b a⋅ = ⋅ ( ) ( ) ( )a b a b a bλ λ λ⋅ = ⋅ = ⋅ ( )a b c a c b c+ ⋅ = ⋅ + ⋅ ( )1 1,a x y= ( )2 2,b x y= 1 2 1 2a b x x y y⋅ = + ( ),a x y= 2 2 2a x y= + 2 2a x y= + ( )1 1,a x y= ( )2 2,b x y= 1 2 1 2 0a b x x y y⊥ ⇔ + = a b ( )1 1,a x y= ( )2 2,b x y= θ a b 1 2 1 2 2 2 2 2 1 1 2 2 cos x x y ya b a b x y x y θ +⋅= = + + ( )cos cos cos sin sinα β α β α β− = + ( )cos cos cos sin sinα β α β α β+ = − ( )sin sin cos cos sinα β α β α β− = − ( )sin sin cos cos sinα β α β α β+ = + ( ) tan tantan 1 tan tan α βα β α β −− = + ⇒ ( )( )tan tan tan 1 tan tanα β α β α β− = − + ⑹ ( ). 25、二倍角的正弦、余弦和正切公式: ⑴ . ⑵ 升幂公式 降幂公式 , . ⑶ . 26、 (后两个不用判断符号,更加好用) 27、合一变形 把两个三角函数的和或差化为“一个三角函数,一个角,一次方”的 形式。 ,其中 . 28、三角变换是运算化简的过程中运用较多的变换,提高三角变换能力,要学会创设条件,灵活运用三角 公式,掌握运算,化简的方法和技能.常用的数学思想方法技巧如下: (1)角的变换:在三角化简,求值,证明中,表达式中往往出现较多的相异角,可根据角与角之间的和差, 倍半,互补,互余的关系,运用角的变换,沟通条件与结论中角的差异,使问题获解,对角的变形如: ① 是 的二倍; 是 的二倍; 是 的二倍; 是 的二倍; ② ;问: ; ; ③ ;④ ; ⑤ ;等等 (2)函数名称变换:三角变形中,常常需要变函数名称为同名函数。如在三角函数中正余弦是基础,通常 化切为弦,变异名为同名。 (3)常数代换:在三角函数运算,求值,证明中,有时需要将常数转化为三角函数值,例如常数“1”的 代换变形有: (4)幂的变换:降幂是三角变换时常用方法,对次数较高的三角函数式,一般采用降幂处理的方法。常用 ( ) tan tantan 1 tan tan α βα β α β ++ = − ⇒ ( )( )tan tan tan 1 tan tanα β α β α β+ = + − sin 2 2sin cosα α α= 222 )cos(sincossin2cossin2sin1 ααααααα ±=±+=±⇒ 2 2 2 2cos2 cos sin 2cos 1 1 2sinα α α α α= − = − = − ⇒ 2sin2cos1,2cos2cos1 22 αααα =−=+ ⇒ 2 cos2 1cos 2 αα += 2 1 cos2sin 2 αα −= 2 2tantan 2 1 tan αα α= − ⇒ ⇒ BxAy ++= )sin( ϕϖ ( )2 2sin cos sinα α α ϕΑ + Β = Α + Β + tanϕ Β= Α α2 α α4 α2 α 2 α 2 α 4 α 2 304560304515 o ooooo =−=−= = 12sin π = 12cos π ββαα −+= )( )4(24 αππαπ −−=+ )4()4()()(2 απαπβαβαα −−+=−++= oo 45tan90sincottancossin1 22 ===+= αααα α α α α α αα αααα 半角公式 sin cos1 cos1 sin cos1 cos1 2tan 2 cos1 2sin;2 cos1 2cos : −=+=+ −±= −±=+±= 降幂公式有: ; 。降幂并非绝对,有时需要升幂,如对无理式 常用升幂化为有理式,常用升幂公式有: ; ; (5)公式变形:三角公式是变换的依据,应熟练掌握三角公式的顺用,逆用及变形应用。 如: ; ; ; ; ; ; ; ; ; = ; = ;(其中 ;) (6)三角函数式的化简运算通常从:“角、名、形、幂”四方面入手; 基本规则是:见切化弦,异角化同角,复角化单角,异名化同名,高次化低次,无理化有理,特殊值 与特殊角的三角函数互化。 如: ; 。 第四章 解三角形 一、知识必备: 1.直角三角形中各元素间的关系: 在△ABC 中,C=90°,AB=c,AC=b,BC=a。 (1)三边之间的关系:a2+b2=c2。(勾股定理) (2)锐角之间的关系:A+B=90°; (3)边角之间的关系:(锐角三角函数定义) sinA=cosB= ,cosA=sinB= ,tanA= 。 αcos1+ _______________tan1 tan1 =− + α α ______________tan1 tan1 =+ − α α ____________tantan =+ βα ___________tantan1 =− βα ____________tantan =− βα ___________tantan1 =+ βα =αtan2 =− α2tan1 =++ oooo 40tan20tan340tan20tan =+ αα cossin =+ αα cossin ba =ϕtan =+ )10tan31(50sin oo =− αα cottan c a c b b a 2.斜三角形中各元素间的关系: 在△ABC 中,A、B、C 为其内角,a、b、c 分别表示 A、B、C 的对边。 (1)三角形内角和:A+B+C=π。所以 sin(A+B)=sinC;cos(A+B)=-cosC;tan(A+B)=-tanC。 ; (2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等 (R 为外接圆半径) (3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两 倍 a2=b2+c2-2bccosA; b2=c2+a2-2cacosB; c2=a2+b2-2abcosC。 (4).三角形的面积公式: = aha= bhb= chc(ha、hb、hc 分别表示 a、b、c 上的高); = absinC= bcsinA= acsinB; 4.解三角形:由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个是边) 求其他未知元素的问题叫做解三角形.广义地,这里所说的元素还可以包括三角形的高、中线、角平 分线以及内切圆半径、外接圆半径、面积等等.主要类型: 5.三角形中的三角变换 三角形中的三角变换,除了应用上述公式和上述变换方法外,还要注意三角形自身的特点。 判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式. 2sin2cos,2cos2sin CBACBA =+=+ RC c B b A a 2sinsinsin === ∆S 2 1 2 1 2 1 ∆S 2 1 2 1 2 1 解三角形的必备知识和典型例题及详解 一、知识必备: 1.直角三角形中各元素间的关系: 在△ABC 中,C=90°,AB=c,AC=b,BC=a。 (1)三边之间的关系:a2+b2=c2。(勾股定理) (2)锐角之间的关系:A+B=90°; (3)边角之间的关系:(锐角三角函数定义) sinA=cosB= ,cosA=sinB= ,tanA= 。 2.斜三角形中各元素间的关系: 在△ABC 中,A、B、C 为其内角,a、b、c 分别表示 A、B、C 的对边。 (1)三角形内角和:A+B+C=π。 (2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等 (R 为外接圆半径) (3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积 的两倍 a2=b2+c2-2bccosA; b2=c2+a2-2cacosB; c2=a2+b2-2abcosC。 3.三角形的面积公式: (1) = aha= bhb= chc(ha、hb、hc 分别表示 a、b、c 上的高); (2) = absinC= bcsinA= acsinB; 4.解三角形:由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个 是边)求其他未知元素的问题叫做解三角形.广义地,这里所说的元素还可以包括三角形的高、 中线、角平分线以及内切圆半径、外接圆半径、面积等等.主要类型: (1)两类正弦定理解三角形的问题: 第 1、已知两角和任意一边,求其他的两边及一角. 第 2、已知两角和其中一边的对角,求其他边角. (2)两类余弦定理解三角形的问题: c a c b b a RC c B b A a 2sinsinsin === ∆S 2 1 2 1 2 1 ∆S 2 1 2 1 2 1 第 1、已知三边求三角. 第 2、已知两边和他们的夹角,求第三边和其他两角. 5.三角形中的三角变换 三角形中的三角变换,除了应用上述公式和上述变换方法外,还要注意三角形自身的特点。 (1)角的变换 因为在△ABC 中,A+B+C=π,所以 sin(A+B)=sinC;cos(A+B)=-cosC;tan(A+B)=-tanC。 ; (2)判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式. 6.求解三角形应用题的一般步骤: (1)分析:分析题意,弄清已知和所求; (2)建模:将实际问题转化为数学问题,写出已知与所求,并画出示意图; (3)求解:正确运用正、余弦定理求解; (4)检验:检验上述所求是否符合实际意义。 二、典例解析 题型 1:正、余弦定理 1(15 北京文科)在 中, , , ,则 . 2.(15 年广东文科)设 的内角 , , 的对边分别为 , , .若 , , ,且 ,则 ( ) A. B. C. D. 3.(15 年安徽文科)在 中, , , ,则 。 4.(15 年福建文科)若 中, , , ,则 _______. 5.(15 年新课标 2 文科)△ABC 中 D 是 BC 上的点,AD 平分 BAC,BD=2DC. (I)求 ; (II)若 ,求 . C∆ΑΒ Α Β C a b c 2a = 2 3c = 3cos 2 Α = b c< b = 3 2 2 2 3 ABC∆ 6=AB 75=∠A 45=∠B =AC ABC∆ 3AC = 045A = 075C = BC = ∠ sin sin B C ∠ ∠ 60BAC∠ = B∠ 2sin2cos,2cos2sin CBACBA =+=+ C∆ΑΒ 3a = 6b = 2 3 π∠Α = ∠Β = 6. (15 年陕西文科) 的内角 所对的边分别为 ,向量 与 平行. (I)求 ; (II)若 求 的面积. 7 .(15 年天津文科)△ABC 中, 内角 A,B,C 所对的边分别为 a,b,c, 已知△ABC 的面积为 , (I)求 a 和 sinC 的值; (II)求 的值. ABC∆ , ,A B C , ,a b c ( , 3 )m a b= (cos ,sin )n A B= A 7, 2a b= = ABC∆ 3 15 12,cos ,4b c A− = = − cos 2 6A π + 题型 2:三角形面积 1、(2013 新课标 2) 的内角 的对边分别为 ,已知 , , ,则 的面积为( ) (A) (B) (C) (D) 2、在 中, , , ,求 的值和 的面积。 题型 3:三角形中的三角恒等变换问题 1. 在△ABC 中,a、b、c 分别是∠A、∠B、∠C 的对边长,已知 a、b、c 成等比数列,且 a2-c2=ac -bc,求∠A 的大小及 的值。 ABC∆ , ,A B C , ,a b c 2b = 6B π= 4C π= ABC∆ 2 3 2+ 3 1+ 2 3 2− 3 1− ∆ABC sin cosA A+ = 2 2 AC = 2 3=AB Atan ∆ABC c Bbsin 题型 4:正、余弦定理判断三角形形状 1.在△ABC 中,若 2cosBsinA=sinC,则△ABC 的形状一定是( ) A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形 题型 5:三角形中求值问题 1、 的三个内角为 ,求当 A 为何值时, 取得最大值,并求 出这个最大值。 ABC∆ A B C、 、 cos 2cos 2 B CA ++ 三、课后跟踪训练 1.(2010 上海文数 18.)若△ 的三个内角满足 ,则△ ( ) (A)一定是锐角三角形. (B)一定是直角三角形. (C)一定是钝角三角形. (D)可能是锐角三角形,也可能是钝角三角形. 2. (2010 天津理数 7 )在△ABC 中,内角 A,B,C 的对边分别是 a,b,c ,若 , ,则 A=( ) (A) (B) (C) (D) 3.(2010 湖北理数)3.在 中,a=15,b=10,A=60°,则 =( ) A - B C - D 4. (2010 广东理数)11. 已知 a,b,c 分别是△ABC 的三个内角 A,B,C 所对的边,若 a=1,b= , A+C=2B,则 sinC= . 5(2009 湖南卷文)在锐角 中, 则 的值等于 , 的取值范 围为 . 6.(2009 全国卷Ⅰ理)在 中,内角 A、B、C 的对边长分别为 、 、 ,已知 , 且 求 b 8.(2009 四川卷文)在 中, 为锐角,角 所对的边分别为 , 且 (I)求 的值;(II)若 ,求 的值。 ABC sin :sin :sin 5:11:13A B C = ABC 2 2 3a b bc− = sin 2 3sinC B= 030 060 0120 0150 ABC∆ cosB 2 2 3 2 2 3 6 3 6 3 3 ABC∆ 1, 2 ,BC B A= = cos AC A AC ABC∆ a b c 2 2 2a c b− = sin cos 3cos sin ,A C A C= ABC∆ A B、 A B C、 、 a b c、 、 5 10sin ,sin5 10A B= = A B+ 2 1a b− = − a b c、 、 9.(2010 陕西文数 17)(本小题满分 12 分) 在△ABC 中,已知 B=45°,D 是 BC 边上的一点, AD=10,AC=14,DC=6,求 AB 的长. 10.(2010 辽宁文数 17)(本小题满分 12 分)在 中, 分别为内角 的对边, 且 (Ⅰ)求 的大小; (Ⅱ)若 ,试判断 的形状. 11.(2010 辽宁理数)在△ABC 中,a, b, c 分别为内角 A, B, C 的对边, 且 (Ⅰ)求 A 的大小; (Ⅱ)求 的最大值. ABC∆ a b c、 、 A B C、 、 2 sin (2 )sin (2 )sina A b c B c b C= + + + A sin sin 1B C+ = ABC∆ 2 sin (2 )sin (2 )sin .a A a c B c b C= + + + sin sinB C+查看更多