- 2021-04-13 发布 |
- 37.5 KB |
- 13页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习小题专练 算法初步、推理与证明作业(全国通用)
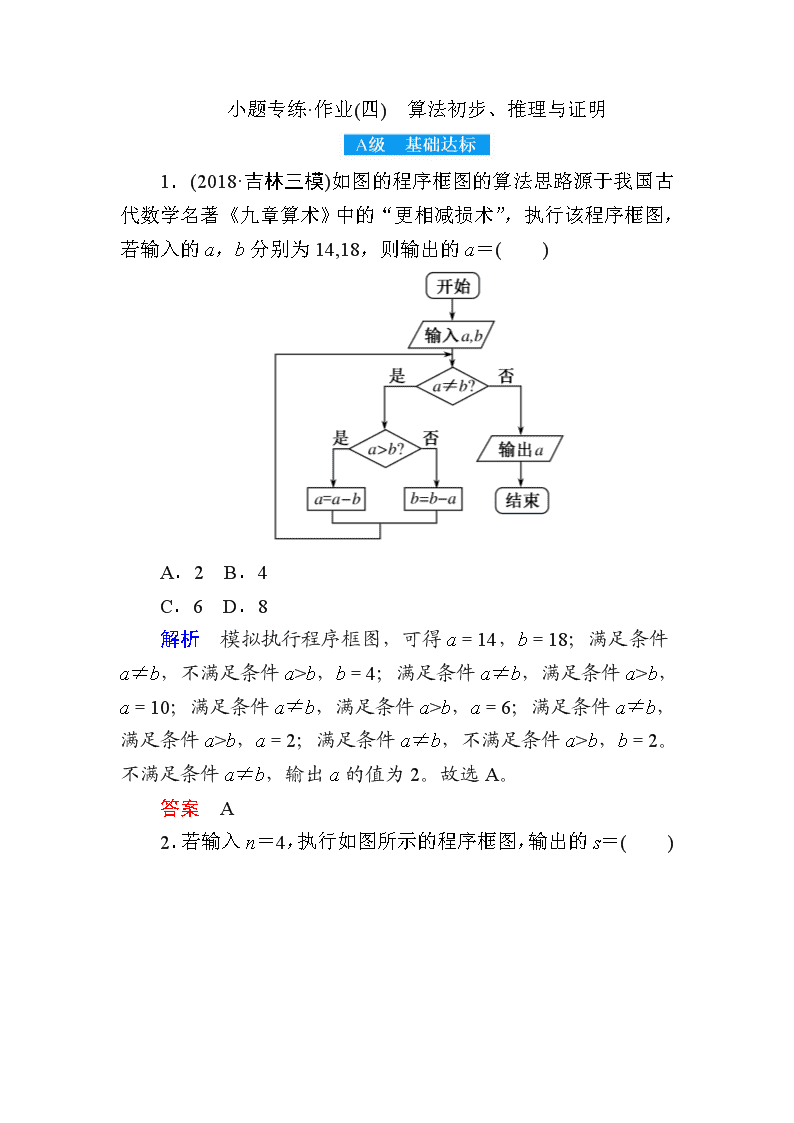
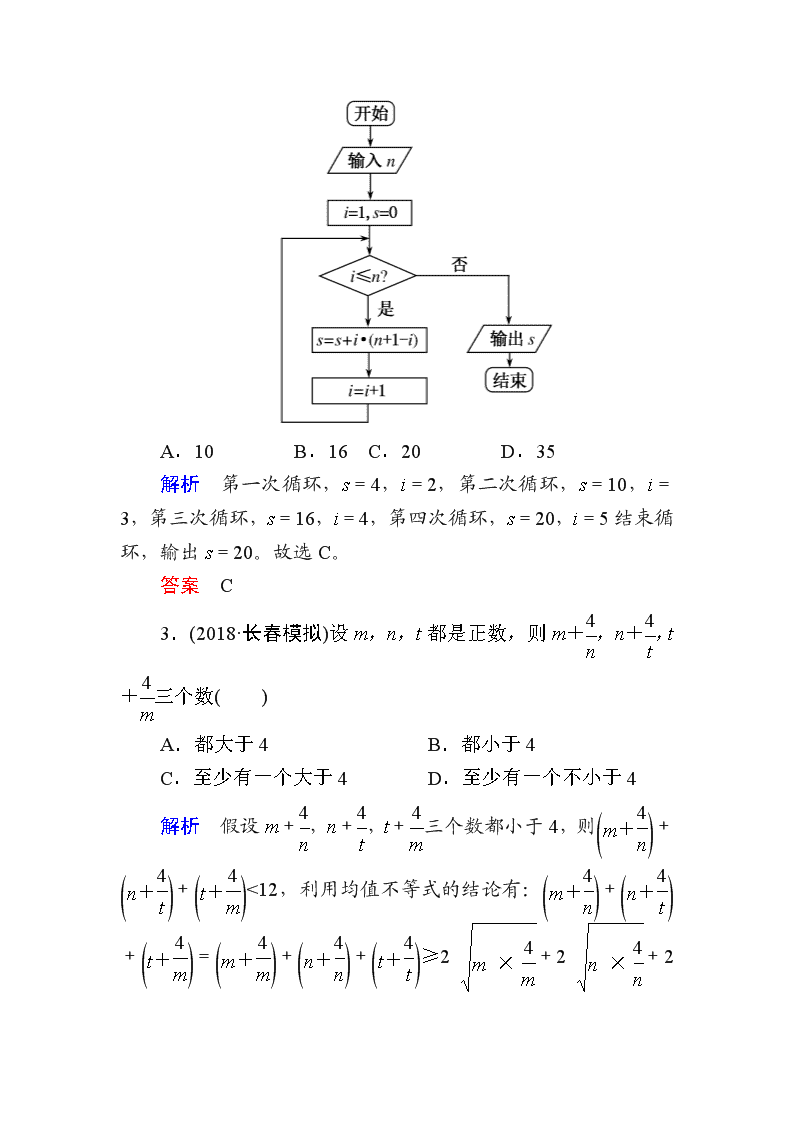
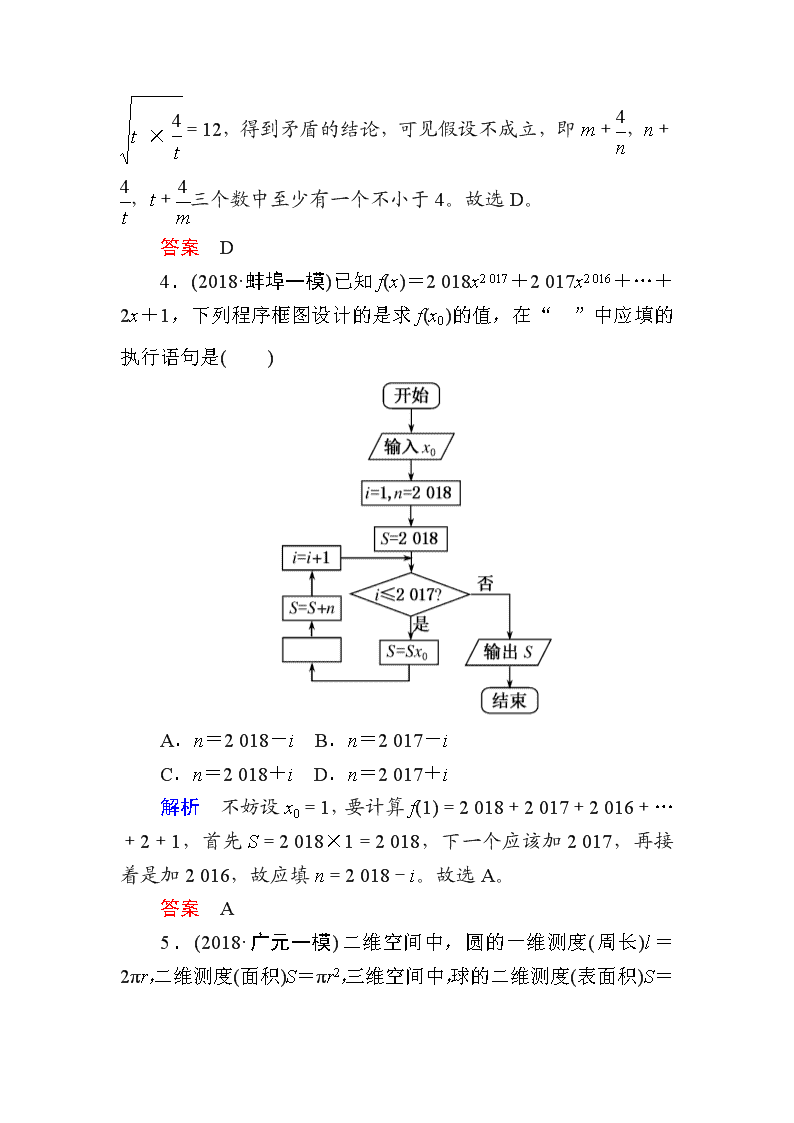
小题专练·作业(四) 算法初步、推理与证明 1.(2018·吉林三模)如图的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a=( ) A.2 B.4 C.6 D.8 解析 模拟执行程序框图,可得a=14,b=18;满足条件a≠b,不满足条件a>b,b=4;满足条件a≠b,满足条件a>b,a=10;满足条件a≠b,满足条件a>b,a=6;满足条件a≠b,满足条件a>b,a=2;满足条件a≠b,不满足条件a>b,b=2。不满足条件a≠b,输出a的值为2。故选A。 答案 A 2.若输入n=4,执行如图所示的程序框图,输出的s=( ) A.10 B.16 C.20 D.35 解析 第一次循环,s=4,i=2,第二次循环,s=10,i=3,第三次循环,s=16,i=4,第四次循环,s=20,i=5结束循环,输出s=20。故选C。 答案 C 3.(2018·长春模拟)设m,n,t都是正数,则m+,n+,t+三个数( ) A.都大于4 B.都小于4 C.至少有一个大于4 D.至少有一个不小于4 解析 假设m+,n+,t+三个数都小于4,则++<12,利用均值不等式的结论有:++=++≥2 +2 +2 =12,得到矛盾的结论,可见假设不成立,即m+,n+,t+三个数中至少有一个不小于4。故选D。 答案 D 4.(2018·蚌埠一模)已知f(x)=2 018x2 017+2 017x2 016+…+2x+1,下列程序框图设计的是求f(x0)的值,在“”中应填的执行语句是( ) A.n=2 018-i B.n=2 017-i C.n=2 018+i D.n=2 017+i 解析 不妨设x0=1,要计算f(1)=2 018+2 017+2 016+…+2+1,首先S=2 018×1=2 018,下一个应该加2 017,再接着是加2 016,故应填n=2 018-i。故选A。 答案 A 5.(2018·广元一模)二维空间中,圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2,三维空间中,球的二维测度(表面积)S =4πr2,三维测度(体积)V=πr3,应用合情推理,若四维空间中,“超球”的三维测度V=8πr3,则其四维测度W=( ) A.2πr4 B.3πr4 C.4πr4 D.6πr4 解析 由题意得,二维空间中,二维测度的导数为一维测度;三维空间中,三维测度的导数为二维测度。由此归纳,在四维空间中,四维测度的导数为三维测度,故W=2πr4。故选A。 答案 A 6.某种树的分枝生长规律如图所示,第1年到第5年的分枝数分别为1,1,2,3,5,则预计第10年树的分枝数为( ) A.21 B.34 C.52 D.55 解析 由2=1+1,3=1+2,5=2+3知,从第三项起,每一项都等于前两项的和,则第6年的分枝数为8,第7年为13,第8年为21,第9年为34,第10年为55。故选D。 答案 D 7.(2018·宁德一模)我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归。问:三女何日相会?”意思是:“ 一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家。三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有( ) A.58 B.59 C.60 D.61 解析 小女儿、二女儿和大女儿回娘家的天数分别是33,25,20,小女儿和二女儿、小女儿和大女儿、二女儿和大女儿回娘家的天数分别是8,6,5,三个女儿同时回娘家的天数是1,所以有女儿回娘家的天数是:33+25+20-(8+6+5)+1=60。故选C。 答案 C 8.(2018·福州模拟)当输入的实数x∈[2,30]时,执行如图所示的程序框图,则输出的x不小于103的概率是________。 解析 设输入的实数为x0,第一次循环为x=2x0+1,n=2;第二次循环为x=4x0+3,n=3;第三次循环为x=8x0+7,n=4。输出8x0+7。因为x0∈[2,30],所以8x0+7∈[23,247]。输出的x不小于103的概率是=。 答案 9.“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图所示的程序框图的算法思路就是来源于“欧几里得算法”,执行该程序框图(图中“a MOD b”表示a除以b所得的余数),若输入的a,b分别为675,125,则输出的a=________。 解析 当a=675,b=125,c=aMODb=50,a=125,b=50,此时c=50,否,c=125MOD50=25,a=50,b=25,此时c=25,否,c=50MOD25=0,a=25,b=0,此时c=0,是,故输出的a=25。 答案 25 10.(2018·安徽模拟)埃及数学中有一个独特现象:除 用一个单独的符号表示以外,其他分数都要写成若干个单分数和的形式。例如=+可以这样理解:假定有两个面包,要平均分给5个人,如果每人,不够,每人,余,再将这分成5份,每人得,这样每人分得+。形如(n=5,7,9,11,…)的分数的分解:=+,=+,=+,…,按此规律,=________;=________(n=5,7,9,11,…)。 解析 =+表示两个面包分给7个人,每人,不够,每人,余,再将这分成7份,每人得,其中4=,28=7×;=+表示两个面包分给9个人,每人,不够,每人,余,再将这分成9份,每人得,其中5=,45=9×,按此规律,表示两个面包分给11个人,每人,不够,每人,余,再将这分成11份,每人得,所以=+,其中6=,66=11×。由以上规律可知,=+。 答案 + + 11.(2018·上饶一模)执行如图所示的程序框图,则输出的结果是( ) A.6 B.7 C.8 D.9 解析 由S=0,n=1,第一次循环:S=0+log2,n=2;第二次循环:S=log2+log2=log2,n=3;第三次循环:S=log2+log2=log2,n=4;第四次循环:S=log2+log2=log2,n=5;第五次循环:S=log2+log2=log2,n=6;第六次循环:S=log2+log2=log2,n=7;第七次循环:S=log2+log2=log2=-3,n=8;符合题意输出n=8。故选C。 答案 C 12.(2018·河南模拟)某程序框图如图所示,该程序运行结束时输出的S的值为( ) A.1 007 B.1 008 C.2 016 D.3 024 解析 循环依次为:a1=1×sin+1=2,S=0+2=2,k=2;a2=2×sin+1=1,S=2+1=3,k=3;a3=3×sin+1=-2,S=3-2=1,k=4;a4=4×sin+1=1,S=1+1=2,k=5;a5=5×sin+1=6,S=6+2=8,k=6;…所以S=(1+1)+(0+1)+(-3+1)+(0+1)+(5+1)+(0+1)+(-7+1)+(0+1)+…+(2 016×0+1)=(-2+4)×=1 008。故选B。 答案 B 13.(2018·益阳、湘潭调研)《数书九章》中给出了“已知三角形三边长求三角形面积的求法” ,填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代人具有很高的数学水平,其求法是“以小斜幂并大斜幂减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积”。若把这段文字写成公式,即S= ,现有周长为2+的△ABC满足sinA∶sinB∶sinC=(-1)∶∶(+1),用上面给出的公式求得△ABC的面积为( ) A. B. C. D. 解析 由正弦定理得sinA∶sinB∶sinC=a∶b∶c=(-1)∶∶(+1),可设三角形的三边分别为a=(-1)x,b=x,c=(+1)x,由题意得(-1)x+x+(+1)x=(2+)x=2+,则x=1,故由三角形的面积公式可得△ABC的面积S= =。故选B。 答案 B 14.(2018·广东一模)大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理。数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,是中华传统文化中隐藏着的世界数学史上第一道数列题。其规律是:偶数项是序号平方再除以2,奇数项是序号平方减1再除以2,其前10项依次是0,2,4,8,12,18,24,32,40,50。如图所示的程序框图是为了得到大衍数列的前100项而设计的,那么在两个“”中,可以先后填入( ) A.n是偶数?,n≥100? B.n是奇数?,n≥100? C.n是偶数?,n>100? D.n是奇数?,n>100? 解析 根据偶数项是序号平方再除以2,奇数项是序号平方减1再除以2可知,第一个“”应该填入“n是奇数?”,执行程序框图。n=1,S=0;n=2,S=2;n=3,S=4;…;n=99,S=;n=100,S=;n=101>100,结束循环,所以第二个“”应该填入“n>100?”。故选D。 答案 D 15.(2018·湖北模拟)“求方程x+x=1的解”有如下解题思路:设f(x)=x+x,则f(x)在R上单调递减,且f(2)=1,所以原方程有唯一解x=2。类比上述解题思路,不等式x6-(x+2)>(x+2)3-x2的解集是________。 解析 不等式x6-(x+2)>(x+2)3-x2变形为x6+x2>(x+2)3+(x+2);令u=x2,v=x+2,则x6+x2>(x+2)3+(x+2)⇔u3+u>v3+v;考察函数f(x)=x3+x,知f(x)在R上为增函数,所以f(u)>f(v),所以u>v;不等式x6+x2>(x+2)3+(x+2)可化为x2>x+2,解得x<-1或x>2;所以不等式的解集为{x|x<-1或x>2}。 答案 {x|x<-1或x>2}查看更多