- 2021-04-13 发布 |
- 37.5 KB |
- 18页

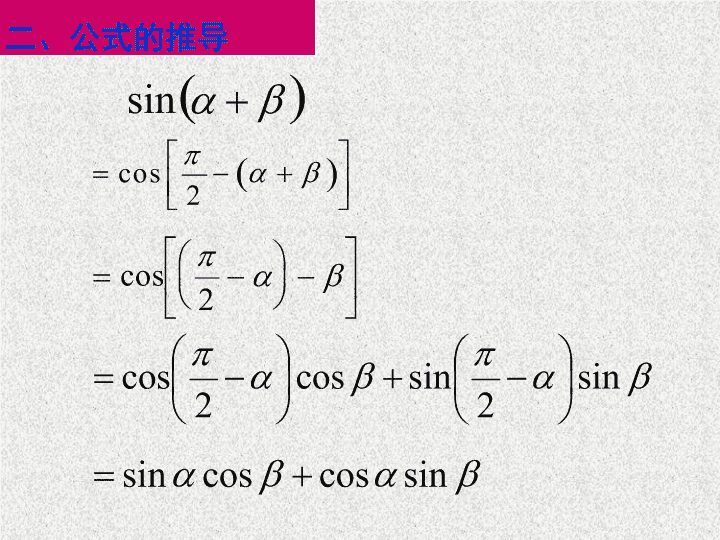
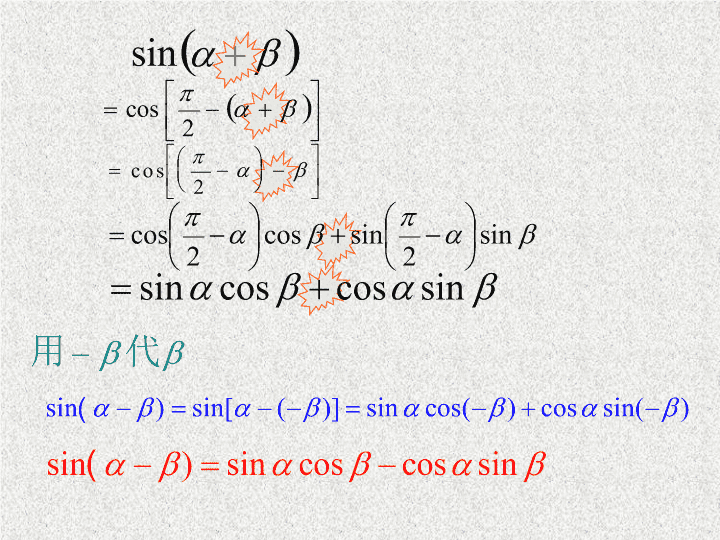
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习两角和与差的正弦、余弦、正切公式课件(18张)(全国通用)
一、复习: cos ( + ) =cos cos – sin sin cos ( – ) =cos cos + sin sin 二、公式的推导 两角和与差的正弦公式 1、两角和的余弦公式 2、两角差的余弦公式 简记: 简记: 两角和的正切公式: 上式中以 代 得 注意: 1 必须在定义域范围内使用上述公式。 2 注意公式的结构,尤其是符号。 即: tan , tan , tan( ± ) 只要有一个不存在就不能使用这个公式,只能(也只需)用诱导公式来解。如 : 已知 tan =2, 求 不能用 两角和与差的正切公式 问 : 如何求 cot( a+ β )? 有关两角和差的余切问题,一般都是将它由同角公 式的倒数关系化为两角和差的正切,用公式来解决. 三 、公式应用 1: 求 tan15 和 tan75 的值: 解: tan15 = tan(45 30 )= tan75 = tan(45 +30 )= 四、练习; 2 、化简: 3 、求值: 答案 : 答案 : (1) 1 (2) -1 五 . 小结 变形: 求下列各式的值: (1) (2) tan17 +tan28 +tan17 tan28 解: 1 原式 = 2 ∵ ∴tan17 +tan28 =tan(17 +28 )(1 tan17 tan28 ) =1 tan17 tan28 ∴ 原式 =1 tan17 tan28 + tan17 tan28 =1 引例 把下列各式化为一个角的三角函数形式 化 为一个角的三角函数形式 令 练习 把下列各式化为一个角的三角函数形式查看更多