2020届二轮复习“立体几何”专题提能课课时作业（全国通用）

2020届二轮复习“立体几何”专题提能课课时作业（全国通用）

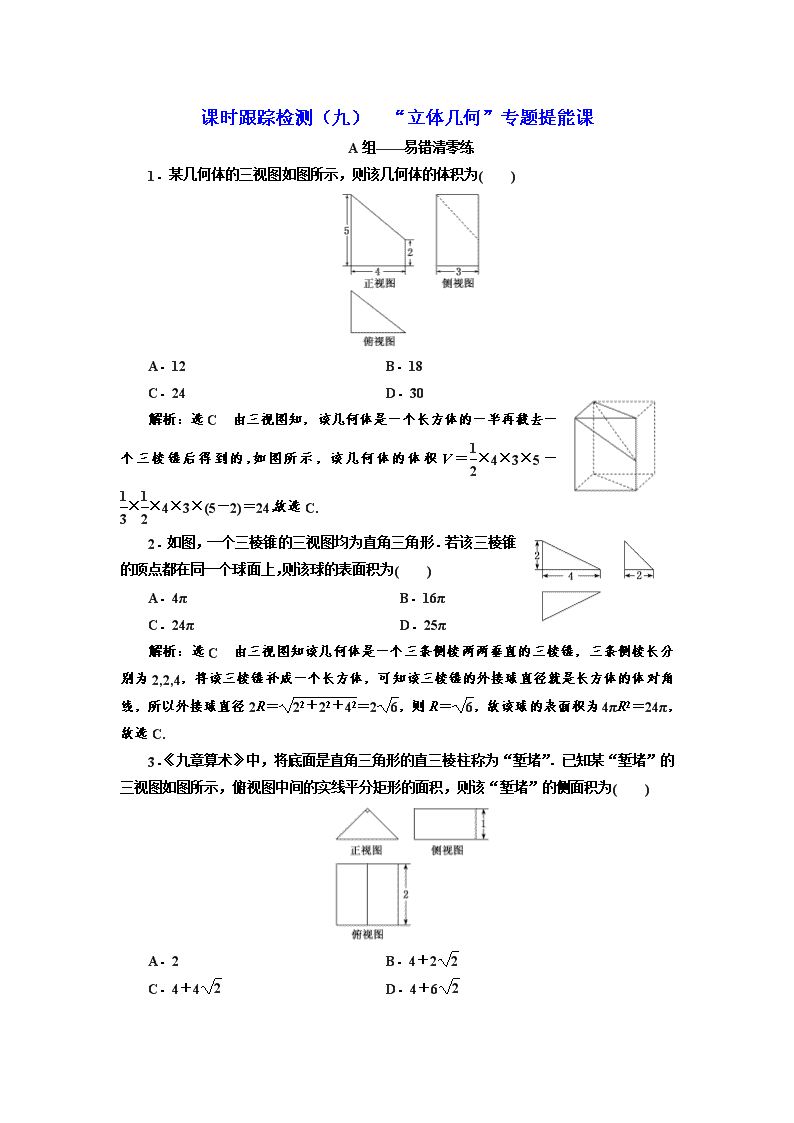
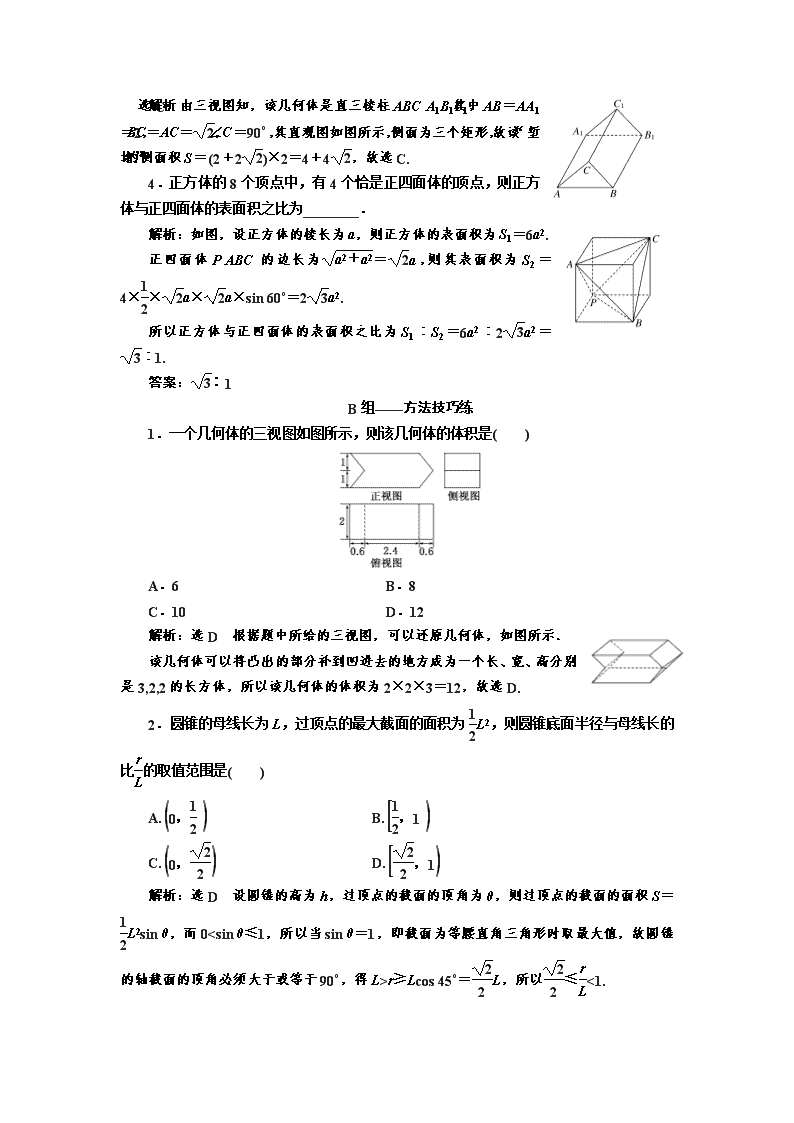
课时跟踪检测（九） “立体几何”专题提能课 A组——易错清零练 ‎1．某几何体的三视图如图所示，则该几何体的体积为(　　)‎ A．12　　　　　　　　 　B．18‎ C．24 D．30‎ 解析：选C　由三视图知，该几何体是一个长方体的一半再截去一个三棱锥后得到的，如图所示，该几何体的体积V＝×4×3×5－××4×3×(5－2)＝24，故选C.‎ ‎2．如图，一个三棱锥的三视图均为直角三角形．若该三棱锥的顶点都在同一个球面上，则该球的表面积为(　　)‎ A．4π　　　　 　 　 B．16π C．24π　　　　　　 D．25π 解析：选C　由三视图知该几何体是一个三条侧棱两两垂直的三棱锥，三条侧棱长分别为2,2,4，将该三棱锥补成一个长方体，可知该三棱锥的外接球直径就是长方体的体对角线，所以外接球直径2R＝＝2，则R＝，故该球的表面积为4πR2＝24π，故选C.‎ ‎3．《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”．已知某“堑堵”的三视图如图所示，俯视图中间的实线平分矩形的面积，则该“堑堵”的侧面积为(　　)‎ A．2 B．4＋2 C．4＋4 D．4＋6 解析：选C　由三视图知，该几何体是直三棱柱ABCA1B‎1C1，其中AB＝AA1＝2，BC＝AC＝，∠C＝90°，其直观图如图所示，侧面为三个矩形，故该“堑堵”的侧面积S＝(2＋2)×2＝4＋4，故选C.‎ ‎4．正方体的8个顶点中，有4个恰是正四面体的顶点，则正方体与正四面体的表面积之比为________．‎ 解析：如图，设正方体的棱长为a，则正方体的表面积为S1＝‎6a2.‎ 正四面体PABC的边长为＝a，则其表面积为S2＝4××a×a×sin 60°＝‎2a2.‎ 所以正方体与正四面体的表面积之比为S1∶S2＝‎6a2∶‎2a2＝∶1.‎ 答案：∶1‎ B组——方法技巧练 ‎1．一个几何体的三视图如图所示，则该几何体的体积是(　　)‎ A．6 B．8‎ C．10 D．12‎ 解析：选D　根据题中所给的三视图，可以还原几何体，如图所示．‎ 该几何体可以将凸出的部分补到凹进去的地方成为一个长、宽、高分别是3,2,2的长方体，所以该几何体的体积为2×2×3＝12，故选D.‎ ‎2．圆锥的母线长为L，过顶点的最大截面的面积为L2，则圆锥底面半径与母线长的比的取值范围是(　　)‎ A. B. C. D. 解析：选D　设圆锥的高为h，过顶点的截面的顶角为θ，则过顶点的截面的面积S＝L2sin θ，而0r≥Lcos 45°＝L，所以≤<1.‎ ‎3．在长方体ABCDA1B‎1C1D1中，AB＝AD＝2，AA1＝1，则点B到平面D‎1AC的距离等于________．‎ 解析：如图，连接BD1，易知D1D就是三棱锥D1ABC的高，AD1＝CD1＝，AC＝2，取AC的中点O，连接D1O，则D1O⊥AC，所以D1O＝＝.‎ 设点B到平面D‎1AC的距离为h，则由VBD‎1AC＝VD1ABC，即S△D‎1AC·h＝S△ABC·D1D，又S△D‎1AC＝D1O·AC＝××2＝，S△ABC＝AB·BC＝×2×2＝2，所以h＝.‎ 答案： ‎4.如图，侧棱垂直于底面的三棱柱ABCA1B‎1C1的底面ABC位于平行四边形ACDE中，AE＝2，AC＝AA1＝4，∠E＝60°，点B在线段ED上．‎ ‎(1)当点B在何处时，平面A1BC⊥平面A1ABB1；‎ ‎(2)点B在线段ED上运动的过程中，求三棱柱ABCA1B‎1C1表面积的最小值．‎ 解：(1)由于三棱柱ABCA1B‎1C1为直三棱柱，则AA1⊥平面ABC，因为BC⊂平面ABC，所以AA1⊥BC.而AA1∩AB＝A，只需BC⊥平面A1ABB1，即AB⊥BC，就有“平面A1BC⊥平面A1ABB‎1”‎．‎ 在平行四边形ACDE中，‎ 因为AE＝2，AC＝AA1＝4，∠E＝60°.‎ 过B作BH⊥AC于H，则BH＝.‎ 若AB⊥BC，有BH2＝AH·CH.‎ 由AC＝4，得AH＝1或3.‎ 两种情况下，B为ED的中点或与点D重合．‎ ‎(2)三棱柱ABCA1B‎1C1的表面积等于侧面积与两个底面积之和．‎ 显然三棱柱ABCA1B‎1C1其底面积和平面A1ACC1的面积为定值，只需保证侧面A1ABB1和侧面B1BCC1面积之和最小即可．‎ 过B作BH⊥AC于H，则BH＝.‎ 令AH＝x，则侧面A1ABB1和侧面B1BCC1面积之和等于4(AB＋BC)＝4[＋]．‎ 其中＋可以表示动点(x,0)到定点(0，－)和(4，)的距离之和，当且仅当x ‎＝2时取得最小值．所以三棱柱的表面积的最小值为2××4×＋42＋4×2＝4＋8＋16.‎ ‎5．(2019届高三·宁波十校联考)如图，在矩形ABCD中，AB＝2，BC＝1，E为CD中点．把△ADE沿AE翻折，使得平面ADE⊥平面ABCE.‎ ‎(1)求证：AD⊥BE；‎ ‎(2)求BD与平面DEC所成角的正弦值．‎ 解：(1)证明：∵在矩形ABCD中，AD＝1，AB＝2，E为CD中点，‎ ‎∴AE＝＝EB，则AE2＋BE2＝AB2，‎ ‎∴BE⊥AE.‎ ‎∵平面ADE⊥平面ABCE，平面ADE∩平面ABCE＝AE，‎ ‎∴BE⊥平面ADE，∴AD⊥BE.‎ ‎(2)法一：取AE的中点O，连接DO，则DO⊥AE.‎ ‎∵平面ADE⊥平面ABCE，平面ADE∩平面ABCE＝AE，‎ ‎∴DO⊥平面ABCE，‎ ‎∴VDBCE＝S△BEC·DO＝××1×1×＝.‎ 连接OB，OC，∵OA＝，AB＝2，∠OAB＝45°，‎ ‎∴在△OAB中，由余弦定理得，‎ OB＝＝，‎ 同理可得OC＝.‎ 在Rt△DOB中，BD＝＝.‎ 在Rt△DOC中，DC＝＝.‎ ‎∵DE＝1，EC＝1，‎ ‎∴在△DEC中，由余弦定理得，cos∠DEC＝＝－，‎ ‎∴∠DEC＝120°，∴S△DEC＝×1×1×＝.‎ 设B到平面DEC的距离为h，‎ ‎∴VBDEC＝×S△DEC×h＝，解得h＝.‎ 设DB与平面DEC所成的角为α，‎ 则sin α＝＝，‎ ‎∴BD与平面DEC所成角的正弦值为.‎ 法二：取AE的中点O，连接DO，则DO⊥AE，‎ ‎∵平面ADE⊥平面ABCE，平面ADE∩平面ABCE＝AE，‎ ‎∴DO⊥平面ABCE，‎ ‎∴以O为坐标原点，OD所在直线为z轴建立如图所示的空间直角坐标系．‎ 则B，D，E，‎ C，‎ ‎∴＝，＝(0,1,0)，‎ ＝，‎ 设m＝(x，y,1)为平面DEC的一个法向量，‎ 则即 取z＝1，可得m＝(－，0,1)，‎ 设BD与平面DEC所成的角为α，‎ ‎∴sin α＝|cos〈，m〉|＝＝，‎ 即BD与平面DEC所成角的正弦值为.‎ C组——创新应用练 ‎1．已知正方体ABCDA1B‎1C1D1的棱长为2，点P是平面AA1D1D的中心，点Q是上底面A1B‎1C1D1上一点，且PQ∥平面AA1B1B，则线段PQ的长的最小值为(　　)‎ A．1 B. C. D. 解析：选A　由PQ∥平面AA1B1B知Q在过点P且平行于平面AA1B1B的平面上，易知点Q在A1D1，B‎1C1中点的连线MN上，故 PQ的最小值为PM＝AA1＝1.‎ ‎2．(2018·昆明模拟)古人采取“用臼舂米”的方法脱去稻谷的外壳，获得可供食用的大米，用于舂米的“臼”多用石头或木头制成．一个“臼”的三视图如图所示，则凿去部分(看成一个简单的组合体)的体积为(　　)‎ A．63π B．72π C．79π D．99π 解析：选A　由三视图得，凿去部分是一个半球与一个圆柱的组合体，其中半球的半径为3，体积为×π×33＝18π，圆柱的底面半径为3，高为5，体积为π×32×5＝45π.所以凿去部分的体积为18π＋45π＝63π.故选A.‎ ‎3．(2018·沈阳质检)在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑，在鳖臑ABCD中，AB⊥平面BCD，且BD⊥CD，AB＝BD＝CD，点P在棱AC上运动，设CP的长度为x，若△PBD的面积为f(x)，则f(x)的图象大致是(　　)‎ 解析：选A　如图，作PQ⊥BC于Q，作QR⊥BD于R，连接PR，则由鳖臑的定义知PQ∥AB，QR∥CD，PQ⊥QR.设AB＝BD＝CD＝1，CP＝x，则＝＝，即PQ＝，又＝＝＝，所以QR＝，所以PR＝＝＝ ，又由题知PR⊥BD，所以f(x)＝ ＝ ，结合选项知选A.‎ ‎4．(2018·长春模拟)已知圆锥的侧面展开图是半径为3的扇形，则该圆锥体积的最大值为________．‎ 解析：由题意得圆锥的母线长为3，设圆锥的底面半径为r，高为h，则h＝，所以圆锥的体积V＝πr2h＝πr2＝π.设f(r)＝9r4－r6(r>0)，则f′(r)＝36r3－6r5，令f′(r)＝36r3－6r5＝6r3(6－r2)＝0，得r＝，所以当00，f(r)单调递增，当r>时，f′(r)<0，f(r)单调递减，所以f(r)max＝f()＝108，所以Vmax＝π×＝2π.‎ 答案：2π ‎5．(2018·惠州模拟)某三棱锥的三视图如图所示，且图中的三个三角形均为直角三角形，则xy的最大值为________．‎ 解析：将三视图还原为如图所示的三棱锥PABC，其中底面ABC是直角三角形，AB⊥BC，PA⊥平面ABC，BC＝2，PA2＋y2＝102，(2)2＋PA2＝x2，所以xy＝x＝x≤＝64，当且仅当x2＝128－x2，即x＝8时取等号，因此xy的最大值是64.‎ 答案：64‎ ‎6．(2019届高三·湖北七市(州)联考)《九章算术》是我国古代内容极为丰富的数学名著，书中将底面为直角三角形的直棱柱称为堑堵，将底面为矩形的棱台称为刍童．在如图所示的堑堵ABMDCP与刍童ABCDA1B‎1C1D1的组合体中，AB＝AD，A1B1＝A1D1.‎ ‎(1)证明：直线BD⊥平面MAC；‎ ‎(2)若AB＝1，A1D1＝2，MA＝，三棱锥AA1B1D1的体积V′＝，求该组合体的体积．‎ 解：(1)证明：由题可知ABMDCP是底面为直角三角形的直棱柱，‎ ‎∴AD⊥平面MAB，‎ ‎∴AD⊥MA，‎ 又MA⊥AB，AD∩AB＝A，‎ ‎∴MA⊥平面ABCD，‎ ‎∴MA⊥BD.‎ 又AB＝AD，‎ ‎∴四边形ABCD为正方形，∴BD⊥AC，‎ 又MA∩AC＝A，‎ ‎∴BD⊥平面MAC.‎ ‎(2)设刍童ABCDA1B‎1C1D1的高为h，‎ 则三棱锥AA1B1D1的体积V′＝××2×2×h＝，∴h＝，‎ 故该组合体的体积V＝×1××1＋×(12＋22＋)×＝＋＝.‎