2018-2019学年安徽省黄山市屯溪第一中学高二下学期期中考试数学（文）试题（解析版）

2018-2019学年安徽省黄山市屯溪第一中学高二下学期期中考试数学（文）试题（解析版）

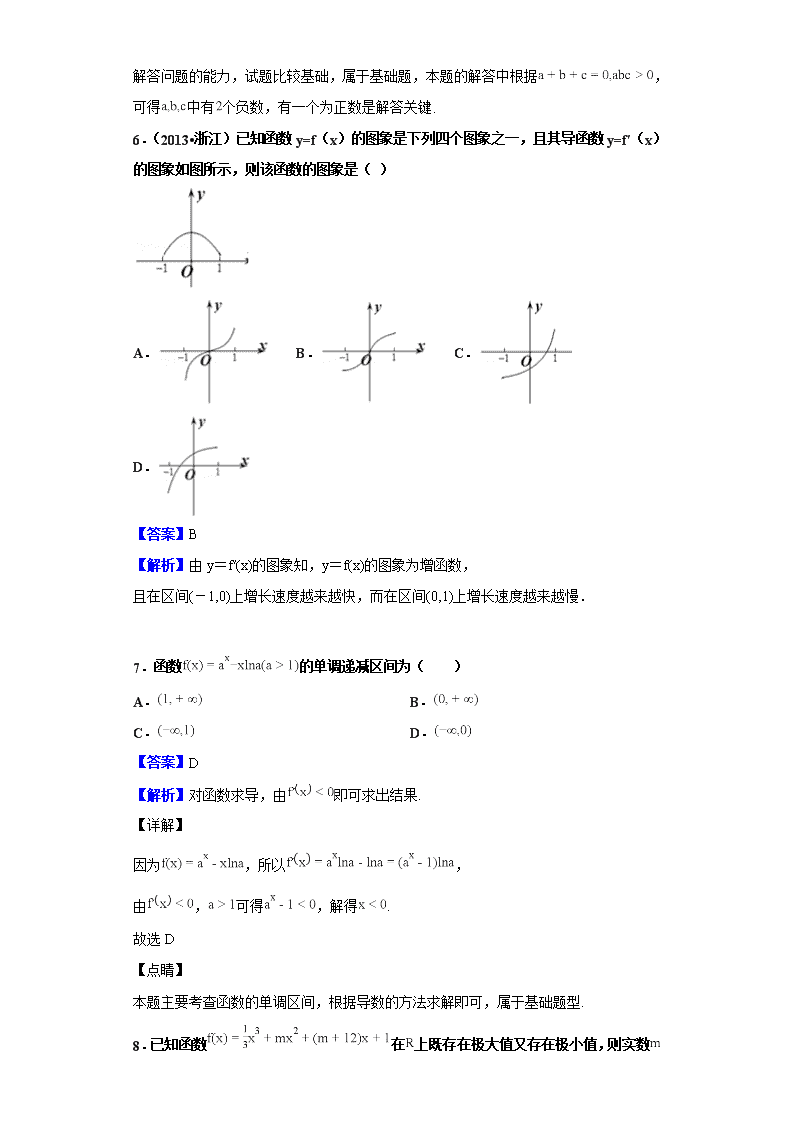
‎2018-2019学年安徽省黄山市屯溪第一中学高二下学期期中考试数学（文）试题 一、单选题 ‎1．函数的极值点为，则的值为（ ）‎ A． B．1 C． D．‎ ‎【答案】C ‎【解析】先对函数求导，根据函数的极值点为，可得，进而可求出结果.‎ ‎【详解】‎ 因为，所以；‎ 又的极值点为，所以，即.‎ 故选C ‎【点睛】‎ 本题主要考查导数的应用，已知极值点求参数的问题，属于基础题型.‎ ‎2．曲线在点处的切线方程是（ ）‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】先对函数求导，求出函数在处的切线斜率，进而可求出结果.‎ ‎【详解】‎ 令，则，‎ 故曲线在点处的切线斜率为，‎ 所以所求切线方程为，整理得.‎ 故选D ‎【点睛】‎ 本题主要考查曲线在某点处的斜线方程，熟记导数的几何意义即可，属于基础题型.‎ ‎3．已知关于两个变量的回归方程为，，则的值为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】先求出的平均值，根据回归直线过样本中心，即可求出结果.‎ ‎【详解】‎ 因为，所以，‎ 又关于两个变量的回归方程为，‎ 所以.‎ 故选B ‎【点睛】‎ 本题主要考查回归直线方程，熟记回归直线必过样本中心即可，属于基础题型.‎ ‎4．一个质点运动的路程与时间的关系，的单位是米（），的单位是秒（），则该质点在时的速度是（ ）／。‎ A． B． C． D．‎ ‎【答案】C ‎【解析】对函数求导，求出，即可得出结果.‎ ‎【详解】‎ 因为，所以，因此.‎ 故选C ‎【点睛】‎ 本题主要考查瞬时变化率，求瞬时速度即是求该点处的导数，属于基础题型.‎ ‎5．已知，且，，则的值（ ）‎ A．一定是正数 B．一定是负数 C．可能是零 D．正、负不能确定 ‎【答案】B ‎【解析】试题分析：根据，可得中有个负数，有一个为正数，不妨设，且，所以，所以，而，所以，故选B.‎ ‎【考点】不等式的性质.‎ ‎【方法点晴】本题主要考查了不等式的性质及其应用，其中解答中涉及不等式的性质及化简，负数的性质以及绝对值的含义等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，试题比较基础，属于基础题，本题的解答中根据，可得中有个负数，有一个为正数是解答关键.‎ ‎6．（2013•浙江）已知函数y=f（x）的图象是下列四个图象之一，且其导函数y=f′（x）的图象如图所示，则该函数的图象是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由y＝f′(x)的图象知，y＝f(x)的图象为增函数，‎ 且在区间(－1,0)上增长速度越来越快，而在区间(0,1)上增长速度越来越慢．‎ ‎7．函数的单调递减区间为（ ）‎ A． B．‎ C． D．‎ ‎【答案】D ‎【解析】对函数求导，由即可求出结果.‎ ‎【详解】‎ 因为，所以，‎ 由，可得，解得.‎ 故选D ‎【点睛】‎ 本题主要考查函数的单调区间，根据导数的方法求解即可，属于基础题型.‎ ‎8．已知函数在上既存在极大值又存在极小值，则实数 的取值范围是（ ）‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】先对函数求导，根据函数在上既存在极大值又存在极小值，得到方程有两不等实根，进而可求出结果.‎ ‎【详解】‎ 因为，‎ 所以，‎ 因为函数在上既存在极大值又存在极小值，‎ 所以只需方程有两不等实根即可，‎ 即，解得或.‎ 故选C ‎【点睛】‎ 本题主要考查导数的应用，对函数求导，根据函数有极值求出参数即可，属于常考题型.‎ ‎9．设，则（ ）‎ A．8 B． C． D．‎ ‎【答案】A ‎【解析】利用导数定义即可得到结果.‎ ‎【详解】‎ ‎，‎ 故选A ‎【点睛】‎ 本题主要考查导数的概念，熟记导数概念以及运算法则即可，属于基础题型.‎ ‎10．设，，，那么、、的大小关系是（ ）‎ A． B．‎ C． D．‎ ‎【答案】B ‎【解析】本题考查不等式的应用.‎ 易知，则的大小关系与大小关系是一致的.‎ 因为 而所以，则； ①‎ 又 因为且 所以 所以 即，所以②‎ 由①②得 故正确答案为 ‎11．已知函数，若恒成立，则的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】先对函数求导，根据恒成立，得到恒成立；配方法求出的最小值即可.‎ ‎【详解】‎ 因为，所以，‎ 由恒成立，可得：恒成立，即恒成立；‎ 又，‎ 所以只需，即可使恒成立.‎ 故选C ‎【点睛】‎ 本题主要考查根据不等式恒成立求参数的问题，一般用分离参数的方法求解，属于常考题型.‎ ‎12．点是曲线上的一个动点，点是曲线上的一个动点，则的最小值为（ ）。‎ A． B．‎ C． D．‎ ‎【答案】A ‎【解析】先由与互为反函数，得到两函数图像关于直线对称；因此只需两点关于直线对称，点到直线距离最小时，最小；设，根据点到直线距离公式、以及导数的方法求解即可.‎ ‎【详解】‎ 因为与互为反函数，所以两函数图像关于直线对称；点是曲线上的一个动点，点是曲线上的一个动点，所以只需两点关于直线对称，点到直线距离最小时，最小；‎ 设，‎ 由点到直线的距离公式可得，‎ 点到直线距离，‎ 令，‎ 则，‎ 由可得：；由可得：，‎ 所以在上单调递减，在上单调递增；‎ 故,‎ 所以，因此的最小值为.‎ 故选A ‎【点睛】‎ 本题主要考查导数的应用、以及函数图像的对称性，熟记导数的方法求函数的最值，灵活掌握点到直线距离公式等，即可求解，属于常考题型.‎ 二、填空题 ‎13．已知，若，，则_________。‎ ‎【答案】‎ ‎【解析】由题意，先求出，，，…，归纳出的表达式，即可求出结果.‎ ‎【详解】‎ 因为，所以，‎ ‎，，…….，‎ 归纳可得，因此.‎ 故答案为 ‎【点睛】‎ 本题主要考查归纳推理，根据题中条件逐步递推即可，属于常考题型.‎ ‎14．在中，，，，则的外接圆半径为，将此结论类比到空间，得到类似的结论为:四面体中，，，，设，,，则四面体的外接球的半径为_____‎ ‎【答案】‎ ‎【解析】在由平面图形到空间图形的类比推理中，一般是由点的性质类比推理线的性质，由线的性质类比推理面的性质，由已知在平面几何中中，，，，则的外接圆半径为，我们可以类比这一性质，直接得出空间中有三条侧棱两两垂直的四面体中类似的结论.‎ ‎【详解】‎ 由已知在中，，，，则的外接圆半径为，‎ 我们可以类比这一性质，推理出：四面体中，，，，设，,，则四面体的外接球的半径为.‎ 故答案为 ‎【点睛】‎ 本题主要考查类比推理，熟记类比推理的概念即可，属于常考题型.‎ ‎15．某厂生产某种产品件的总成本（单位：万元），又知产品单价的平方与产品件数成反比，生产件这样的产品单价为万元，则产量定为______件时总利润最大。‎ ‎【答案】‎ ‎【解析】先设产品单价为，根据产品单价的平方与产品件数成反比，所以，由生产件这样的产品单价为万元，求出；再记生产件产品时，总利润为 ‎,‎ 可得，用导数的方法研究其单调性，即可求出结果.‎ ‎【详解】‎ 设产品单价为，因为产品单价的平方与产品件数成反比，所以,（其中为非零常数），‎ 又生产件这样的产品单价为万元，所以，故，‎ 记生产件产品时，总利润为,‎ 所以,‎ 则，‎ 由得：，‎ 由得：，‎ 故函数在上单调递增，在上单调递减，‎ 因此当时，取最大值.‎ 即产量定为件时，总利润最大。‎ 故答案为 ‎【点睛】‎ 本题主要考查函数的应用，根据题意建立等量关系，由导数方法研究函数单调性即可得出结果，属于常考题型.‎ ‎16．已知定义在的函数的导函数，且满足，，则的解集为__________。‎ ‎【答案】‎ ‎【解析】先由换元法令，得，将化为；再令，用导数方法结合题中条件判断单调性，再由，求出的范围，进而可得出原不等式 解集.‎ ‎【详解】‎ 令，得，所以不等式可化为，即；‎ 令，则，‎ 因为定义在的函数的导函数，且满足，‎ 所以，‎ 因此函数在上单调递增；‎ 又，所以，‎ 因此由得，，所以，‎ 故，解得.‎ 故答案为 ‎【点睛】‎ 本题主要考查导数的应用，通常需用换元法将原式变形，再构造函数，用导数方法研究新函数的单调性等，即可求解，属于常考题型.‎ 三、解答题 ‎17．有人记录了某种设备的保养和维修费用（万元）与使用年数（年）的前年的数据如下表所示。‎ 使用年数 保养和维修费用 ‎⑴由与的散点图分析可知，与具有线性相关，求回归直线方程。‎ ‎⑵根据⑴所得的方程，如果这台设备要使用年，问这台设备第年大约需要多少保养和维修费用？（参考公式：）‎ ‎【答案】(1) (2) 万元 ‎【解析】（1）根据题中数据求出，，根据求出，再得到，即可得出结果；‎ ‎（2）将代入（1）的结果即可求出预测值.‎ ‎【详解】‎ ‎⑴由题意可得：，‎ 所以，‎ 因此回归直线的方程为：；‎ ‎⑵根据⑴所得的方程，当时，（万元）。‎ 这台设备第年大约需要保养和维修费大约为万元。‎ ‎【点睛】‎ 本题主要考查线性回归分析，熟记最小二乘法求，即可，属于常考题型.‎ ‎18．某大型活动即将举行，为了做好接待工作，组委会招募了名男志愿者和名女志愿者，调查发现，男、女志愿者中分别有人和人喜爱运动，其余人不喜爱运动。‎ ‎⑴根据以上数据完成以下列联表：‎ 喜爱运动 不喜爱运动 总计 男志愿者 女志愿者 总计 ‎⑵根据列联表判断能否有℅的把握认为性别与喜爱运动有关？‎ 下面的临界值表供参考：‎ ‎ ‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ K ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎(参考公式： ，其中)‎ ‎【答案】(1)见解析；(2)见解析 ‎【解析】（1）根据题中数据可直接完善列联表；‎ ‎（2）先由，求出，再由临界值表，即可得出结果.‎ ‎【详解】‎ ‎⑴完成以下列联表：‎ 喜爱运动 不喜爱运动 总计 男志愿者 女志愿者 总计 ‎⑵‎ 所以我们没有℅的把握认为性别与喜爱运动有关。‎ ‎【点睛】‎ 本题主要考查独立性检验，完善列联表以及求的值，是常考内容，属于基础题型.‎ ‎19．设, 且，求证：‎ ‎⑴；‎ ‎⑵。‎ ‎【答案】(1) 见证明；(2) 见证明 ‎【解析】(1)根据，得到；由基本不等式可得，进而可证明结论成立；‎ ‎(2)先由基本不等式得到，进而可得，再由题中条件，即可求出结果.‎ ‎【详解】‎ ‎⑴因为, 且，‎ 所以，即，‎ 又，‎ 所以，‎ 因此。‎ ‎⑵由基本不等式可得，‎ ‎，所以 又，‎ 所以.‎ ‎【点睛】‎ 本题主要考查不等式的证明，灵活运用基本不等式即可，属于常考题型.‎ ‎20．设，且，，，用反证法证明：至少有一个大于。‎ ‎【答案】见证明 ‎【解析】用反证法，先假设结论不成立，即，得到，再由题中条件求出的范围，推出矛盾，即可得结论成立.‎ ‎【详解】‎ 证明：（反证法） 假设结论不成立，即 ，‎ 而 这与相矛盾 故至少有一个大于。‎ ‎【点睛】‎ 本题主要考查反证法，熟记反证的思想，即可求解，属于常考题型.‎ ‎21．已知函数。‎ ‎⑴若有极值，求的取值范围；‎ ‎⑵当在处取得极值时，对于内的任意两个值，都有。‎ ‎【答案】(1) (2)见证明 ‎【解析】（1）先对函数求导，根据函数有极值可得，有两不等实根，即，求解即可得出结果；‎ ‎（2）先由在处取得极值，求出，进而判断函数单调性，求出函数最值，即可得出结论成立.‎ ‎【详解】‎ ‎⑴‎ 又有极值 或。‎ 所以的取值范围为。‎ ‎⑵由于在处取得极值，所以 令，则或；‎ 令，则。‎ 所以的最大值为和中的一个，‎ 的最小值为和中的一个，‎ ‎【点睛】‎ 本题主要考查导数的应用，通常需要对函数求导，根据函数有极值求参数，熟记导数的方法研究函数的单调性、极值等即可，属于常考题型.‎ ‎22．已知函数，，其中都是常数。‎ ‎⑴曲线和曲线在它们交点处具有公共切线，求的值；‎ ‎⑵当时，求函数的单调区间。‎ ‎【答案】(1) (2)见解析 ‎【解析】（1）由题意得到，分别对与求导，根据题意列出方程组，即可求出结果；‎ ‎（2）当时，令，‎ 对求导，分别讨论，，即可得出结果.‎ ‎【详解】‎ ‎⑴ ，‎ ‎ ，‎ 依题意有 ‎ ‎⑵当时，令 ‎ ，则 若，则 在上是增函数； ‎ 若，令 或 令 ‎ 即的单调递增区间是，，单调递减区间为； ‎ 若，令 或 令 ‎ 即的单调递增区间是，，单调递减区间为。‎ 故当时，的单调递增区间是；‎ 当时，的单调递增区间是，，单调递减区间为；‎ 当时，的单调递增区间是，，单调递减区间为。‎ ‎【点睛】‎ 本题主要考查导数的应用，熟记导数的几何意义以及导数的方法求函数单调区间即可，属于常考题型.‎