- 2021-02-26 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018年重庆市九校联盟高考数学一模试卷(文科)
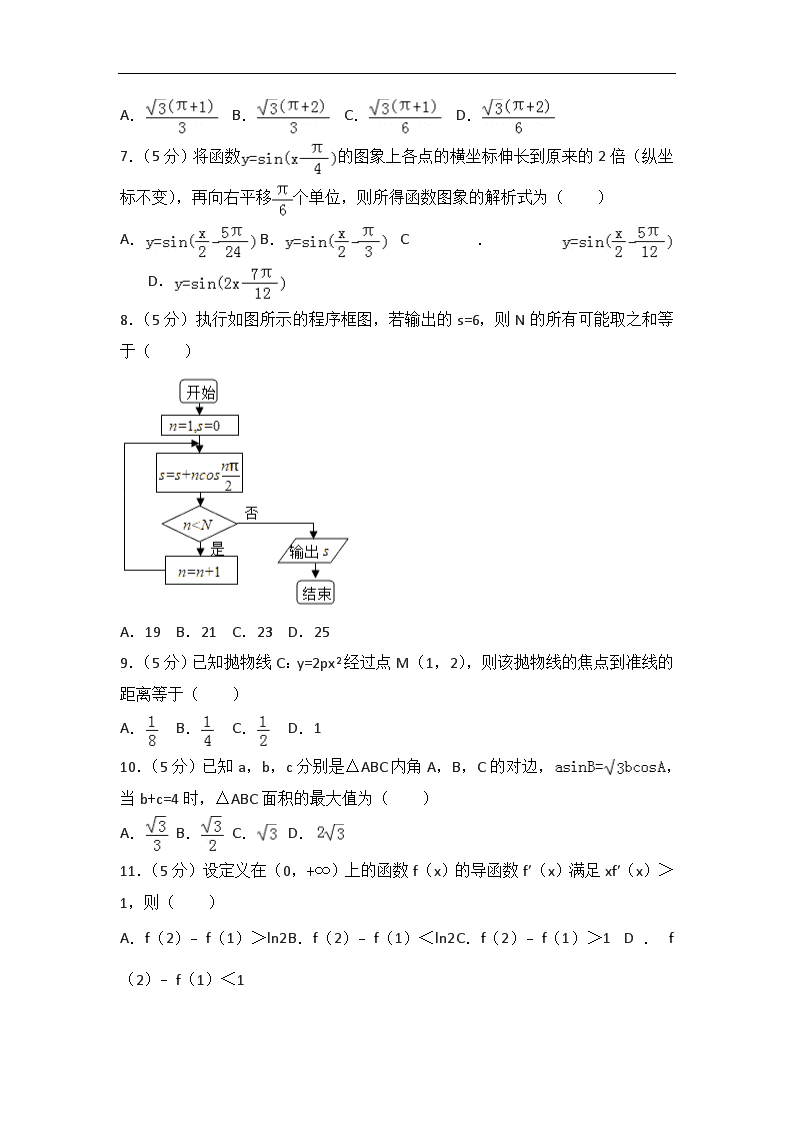
2018年重庆市九校联盟高考数学一模试卷(文科) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)已知集合A={﹣1,0,1,2},,则A∩B=( ) A.{0,1} B.{1,2} C.{﹣1,0} D.{﹣1,2} 2.(5分)已知i为虚数单位,且(1+i)z=﹣1,则复数z对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.(5分)的值为( ) A.﹣1 B. C. D. 4.(5分)已知随机事件A,B发生的概率满足条件,某人猜测事件发生,则此人猜测正确的概率为( ) A.1 B. C. D.0 5.(5分)双曲线的一个焦点为F,过点F作双曲线C的渐近线的垂线,垂足为A,且交y轴于B,若A为BF的中点,则双曲线的离心率为( ) A. B. C.2 D. 6.(5分)某几何体的三视图如图所示,其正视图和侧视图是全等的正三角形,其俯视图中,半圆的直径是等腰直角三角形的斜边,若半圆的直径为2,则该几何体的体积等于( ) A. B. C. D. 7.(5分)将函数的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位,则所得函数图象的解析式为( ) A. B. C. D. 8.(5分)执行如图所示的程序框图,若输出的s=6,则N的所有可能取之和等于( ) A.19 B.21 C.23 D.25 9.(5分)已知抛物线C:y=2px2经过点M(1,2),则该抛物线的焦点到准线的距离等于( ) A. B. C. D.1 10.(5分)已知a,b,c分别是△ABC内角A,B,C的对边,,当b+c=4时,△ABC面积的最大值为( ) A. B. C. D. 11.(5分)设定义在(0,+∞)上的函数f(x)的导函数f′(x)满足xf′(x)>1,则( ) A.f(2)﹣f(1)>ln2 B.f(2)﹣f(1)<ln2 C.f(2)﹣f(1)>1 D.f(2)﹣f(1)<1 12.(5分)设m,θ∈R,则的最小值为( ) A.3 B.4 C.9 D.16 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.(5分)已知向量,,且,则= . 14.(5分)已知实数x,y满足,则目标函数z=3x+y的最大值为 . 15.(5分)已知奇函数f(x)的图象关于直线x=3对称,当x∈[0,3]时,f(x)=﹣x,则f(﹣16)= . 16.(5分)半径为R的球O放置在水平平面α上,点P位于球O的正上方,且到球O表面的最小距离为R,则从点P发出的光线在平面α上形成的球O的中心投影的面积等于 . 三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(12分)已知Sn是公差不为0的等差数列{an}的前n项和,S5=35,a1,a4,a13成等比数列. (1)求数列{an}的通项公式; (2)求数列的前n项和Tn. 18.(12分)某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”,从辖区住户的离退休老人中随机抽取了100位老人进行调查,获得了每人每天的平均户外“活动时间”(单位:小时),活动时间按照[0,0.5)、[0.5,1)、…、[4,4.5] 从少到多分成9组,制成样本的频率分布直方图如图所示. (1)求图中a的值; (2)估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数; (3)在[1,1.5)、[1.5,2)这两组中采用分层抽样抽取7人,再从这7人中随机抽取2人,求抽取的两人恰好都在同一个组的概率. 19.(12分)如图,直三棱柱ABC﹣A1B1C1中,侧面ABB1A1是正方形,A1B1⊥A1C1. (1)证明:AB1⊥BC1; (2)当三棱锥A﹣A1B1C1的体积为2,AA1=2时,求点C到平面AB1C1的距离. 20.(12分)如图,A,B是椭圆长轴的两个端点,P,Q是椭圆C上都不与A,B重合的两点,记直线BQ,AQ,AP的斜率分别是kBQ,kAQ,kAP. (1)求证:; (2)若kAP=4kBQ,求证:直线PQ恒过定点,并求出定点坐标. 21.(12分)设函数f(x)=ex﹣asinx. (1)当a=1时,证明:∀x∈(0,+∞),f(x)>1; (2)若∀x∈[0,+∞),f(x)≥0都成立,求实数a的取值范围. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程] 22.(10分)已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程为ρ=4cosθ,直线l的参数方程为(t为参数). (1)求直线l和圆C的直角坐标方程; (2)设点P(2,1),直线l与圆C交于A,B两点,求|PA|•|PB|的值. [选修4-5:不等式选讲] 23.已知函数f(x)=|2x+1|. (1)解不等式f(x)>x+5; (2)若对于任意x,y∈R,有,,求证:f(x)<1. 2018年重庆市九校联盟高考数学一模试卷(文科) 参考答案与试题解析 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)已知集合A={﹣1,0,1,2},,则A∩B=( ) A.{0,1} B.{1,2} C.{﹣1,0} D.{﹣1,2} 【解答】解:由或x<0, 即B={x|x>1或x<0}, ∵A={﹣1,0,1,2}, ∴A∩B={﹣1,2}, 故选D. 2.(5分)已知i为虚数单位,且(1+i)z=﹣1,则复数z对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【解答】解:由(1+i)z=﹣1,得z=﹣, ∴复数z对应的点的坐标为(),位于第二象限, 故选:B. 3.(5分)的值为( ) A.﹣1 B. C. D. 【解答】解:∵, 故选:B. 4.(5分)已知随机事件A,B发生的概率满足条件,某人猜测事件发生,则此人猜测正确的概率为( ) A.1 B. C. D.0 【解答】解:∵事件与事件A∪B是对立事件, 随机事件A,B发生的概率满足条件, ∴某人猜测事件发生,则此人猜测正确的概率为: . 故选:C. 5.(5分)双曲线的一个焦点为F,过点F作双曲线C的渐近线的垂线,垂足为A,且交y轴于B,若A为BF的中点,则双曲线的离心率为( ) A. B. C.2 D. 【解答】解:根据题意,双曲线的焦点在x轴上, 过点F作双曲线C的渐近线的垂线,垂足为A, 且交y轴于B,如图 若A为BF的中点,则OA垂直平分BF, 则双曲线C的渐近线与x轴的夹角为, 即双曲线的渐近线方程为y=±x, 则有a=b, 则c==a, 则双曲线的离心率e==; 故选A. 6.(5分)某几何体的三视图如图所示,其正视图和侧视图是全等的正三角形,其俯视图中,半圆的直径是等腰直角三角形的斜边,若半圆的直径为2,则该几何体的体积等于( ) A. B. C. D. 【解答】解:解:由已知中的三视图可得该几何体是一个半圆锥和三棱锥的组合体, 其体积为, 故选D. 7.(5分)将函数的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位,则所得函数图象的解析式为( ) A. B. C. D. 【解答】解:把函数经伸长到原来的2倍(纵坐标不变), 可得,再向右平移个单位,得=的图象, 故选:B. 8.(5分)执行如图所示的程序框图,若输出的s=6,则N的所有可能取之和等于( ) A.19 B.21 C.23 D.25 【解答】解:模拟程序的运行,可得程序框图的功能是计算并输出S=cos+2cos+3cos+…得值, 由题意,S=cos+2cos+3cos+…=6, 可得:0﹣2+4﹣6+8﹣10…=6, 可得:S=cos+2cos+3cos+…+12cos, 或S=cos+2cos+3cos+…+12cos+13cos, 可得:N的可取值有且只有12,13,其和为25, 故选:D. 9.(5分)已知抛物线C:y=2px2 经过点M(1,2),则该抛物线的焦点到准线的距离等于( ) A. B. C. D.1 【解答】解:根据题意,抛物线C:y=2px2经过点M(1,2), 则有2=2p×12,解可得p=1, 则抛物线的方程为y=2x2,其标准方程为x2=y, 其焦点坐标为(0,),准线方程为y=﹣, 该抛物线的焦点到准线的距离等于; 故选:B. 10.(5分)已知a,b,c分别是△ABC内角A,B,C的对边,,当b+c=4时,△ABC面积的最大值为( ) A. B. C. D. 【解答】解:由:,利用正弦定理可得:sinAsinB=sinBcosA, 又sinB≠0,可得:tanA=, 因为:A∈(0,π), 所以:A=. 故,(当且仅当b=c=2时取等号), 故选:C. 11.(5分)设定义在(0,+∞)上的函数f(x)的导函数f′(x)满足xf′(x)>1,则( ) A.f(2)﹣f(1)>ln2 B.f(2)﹣f(1)<ln2 C.f(2)﹣f(1)>1 D.f(2)﹣f(1)<1 【解答】解:根据题意,函数f(x)的定义域为(0,+∞), 即x>0,则, 故,即f(2)﹣f(1)>ln2, 故选A. 12.(5分)设m,θ∈R,则的最小值为( ) A.3 B.4 C.9 D.16 【解答】解:令点P(2﹣m,2+m),Q(cosθ,sinθ). 点P在直线上,点Q的轨迹为单位圆:x2+y2=1. 因此的最小值为:单位圆上的点到直线的距离的平方, 故其最小值==(4﹣1)2=9. 故选:C. 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.(5分)已知向量,,且,则= 10 . 【解答】解:向量,,且, ∴1×m﹣(﹣2)×2=0, 解得m=﹣4, ∴=1×2+(﹣2)×(﹣4)=10. 故答案为:10. 14.(5分)已知实数x,y满足,则目标函数z=3x+y的最大值为 . 【解答】解:实数x,y满足作出可行域,目标函数z=3x+y,由解得A, 的最优解对应的点为, 故. 故答案为:. 15.(5分)已知奇函数f(x)的图象关于直线x=3对称,当x∈[0,3]时,f(x)=﹣x,则f(﹣16)= 2 . 【解答】解:根据题意,函数f(x)的图象关于直线x=3对称, 则有f(x)=f(6﹣x), 又由函数为奇函数,则f(﹣x)=﹣f(x), 则有f(x)=﹣f(6﹣x)=f(x﹣12), 则f(x)的最小正周期是12, 故f(﹣16)=f(﹣4)=﹣f(4)=﹣f(2), 即f(﹣16)=﹣(﹣2)=2; 故答案为:2. 16.(5分)半径为R的球O放置在水平平面α上,点P位于球O的正上方,且到球O表面的最小距离为R,则从点P发出的光线在平面α上形成的球O的中心投影的面积等于 3πR2 . 【解答】解:∵半径为R的球O放置在水平平面α上,点P位于球O的正上方,且到球O表面的最小距离为R, ∴轴截面如下图所示, , ∴从点P发出的光线在平面α上形成的球O的中心投影的面积为: S=3πR2. 故答案为:3πR2. 三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(12分)已知Sn是公差不为0的等差数列{an}的前n项和,S5=35,a1,a4,a13成等比数列. (1)求数列{an}的通项公式; (2)求数列的前n项和Tn. 【解答】解:(1)S5=35⇒5a3=35⇒a3=7, 设公差为d,a1,a4,a13成等比数列 (舍去d=0). ∴an=2n+1. (2), ∴. ∴, =. 18.(12分)某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”,从辖区住户的离退休老人中随机抽取了100位老人进行调查,获得了每人每天的平均户外“活动时间”(单位:小时),活动时间按照[0,0.5)、[0.5,1)、…、[4,4.5]从少到多分成9组,制成样本的频率分布直方图如图所示. (1)求图中a的值; (2)估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数; (3)在[1,1.5)、[1.5,2)这两组中采用分层抽样抽取7人,再从这7人中随机抽取2人,求抽取的两人恰好都在同一个组的概率. 【解答】(本小题满分12分) 解:(1)由频率分布直方图,可知,平均户外“活动时间”在[0,0.5)的频率为0.08×0.5=0.04. 同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5)等组的频率分别为0.08,0.20,0.25,0.07,0.04,0.02, 由1﹣(0.04+0.08+0.20+0.25+0.07+0.04+0.02)=0.5×a+0.5×a. 解得a=0.30. (2)设中位数为m小时. 因为前5组的频率之和为0.04+0.08+0.15+0.20+0.25=0.72>0.5, 而前4组的频率之和为0.04+0.08+0.15+0.20=0.47<0.5,所以2≤m<2.5. 由0.50×(m﹣2)=0.5﹣0.47,解得m=2.06. 故可估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数为2.06小时. (3)由题意得平均户外活动时间在[1,1.5),[1.5,2)中的人数分别有15人、20人, 按分层抽样的方法分别抽取3人、4人,记作A,B,C及a,b,c,d, 从7人中随机抽取2人,共有21种,分别为: (A,B),(A,C),(A,a),(A,b),(A,c),(A,d),(B,C),(B,a),(B,b),(B,c),(B,d), (C,a),(C,b),(C,c),(C,d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d), 同时在同一组的有: (A,B),(A,C),(B,C),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d).共9种, 故抽取的两人恰好都在同一个组的概率. 19.(12分)如图,直三棱柱ABC﹣A1B1C1中,侧面ABB1A1是正方形,A1B1⊥A1C1. (1)证明:AB1⊥BC1; (2)当三棱锥A﹣A1B1C1的体积为2,AA1=2时,求点C到平面AB1C1的距离. 【解答】(1)证明:如图,由ABB1A1是正方形得AB1⊥BA1, 在直三棱柱ABC﹣A1B1C1中,AA1⊥A1C1,又AA1∩A1B1=A1, ∴A1C1⊥平面ABB1A1,且AB1⊂平面ABB1A1, 故AB1⊥A1C1,且BA1∩A1C1=A1, 故AB1⊥平面BA1C1,且BC1⊂平面BA1C1, ∴AB1⊥BC1. (2)解:∵三棱锥A﹣A1B1C1的体积为2,得. 如图,设AB1∩BA1=O,连接OC1,则, 设点A1到平面AB1C1的距离为d, 则, 由对称性知:点C到平面AB1C1的距离为. 20.(12分)如图,A,B是椭圆长轴的两个端点,P,Q是椭圆C上都不与A,B重合的两点,记直线BQ,AQ,AP的斜率分别是kBQ,kAQ,kAP. (1)求证:; (2)若kAP=4kBQ,求证:直线PQ恒过定点,并求出定点坐标. 【解答】证明:(1)设Q(x1,y1), 由椭圆,得B(﹣2,0),A(2,0), ∴; (2)由(1)知:. 设P(x2,y2),直线PQ:x=ty+m, 代入x2+4y2=4,得(t2+4)y2+2mty+m2﹣4=0, ∴,, 由kAP•kAQ=﹣1得:(x1﹣2)(x2﹣2)+y1y2=0, ∴, ∴(t2+1)(m2﹣4)+(m﹣2)t(﹣2mt)+(m﹣2)2(t2+4)=0, ∴5m2﹣16m+12=0,解得m=2或m=. ∵m≠2,∴, ∴直线PQ:,恒过定点. 21.(12分)设函数f(x)=ex﹣asinx. (1)当a=1时,证明:∀x∈(0,+∞),f(x)>1; (2)若∀x∈[0,+∞),f(x)≥0都成立,求实数a的取值范围. 【解答】(1)证明:由a=1知f(x)=ex﹣sinx, 当x∈[0,+∞)时,f'(x)=ex﹣cosx≥0(当且仅当x=0时取等号), 故f(x)在[0,+∞)上是增函数, 又f(0)=1,故∀x∈(0,+∞),f(x)>f(0)=1, 即:当a=1时,∀x∈(0,+∞),f(x)>1. (2)解:当a=0时,f(x)=ex,符合条件; 当a>0时,设与y2=asinx在点(x0,y0)处有公切线, 则, 故; 当a<0时,设与y2=asinx在点(x0,y0)处有公切线, 同法可得; 综上所述,实数a的取值范围是. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程] 22.(10分)已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程为ρ=4cosθ,直线l的参数方程为(t为参数). (1)求直线l和圆C的直角坐标方程; (2)设点P(2,1),直线l与圆C交于A,B两点,求|PA|•|PB|的值. 【解答】(本小题满分10分)【选修4﹣4:坐标系与参数方程】 解:(1)∵直线l的参数方程为(t为参数). ∴直线l的直角坐标方程为, ∵圆C的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ, ∴圆C的直角坐标方程为x2+y2﹣4x=0. (2)将代入x2+y2﹣4x=0, 整理得:, ∴|PA|•|PB|=|t1|•|t2|=|t1•t2|=3. [选修4-5:不等式选讲] 23.已知函数f(x)=|2x+1|. (1)解不等式f(x)>x+5; (2)若对于任意x,y∈R,有,,求证:f(x)<1. 【解答】(Ⅰ)解:f(x)>x+5⇒|2x+1|>x+5 ⇒2x+1>x+5或2x+1<﹣x﹣5, ∴解集为{x|x>4或x<﹣2}. (Ⅱ)证明:. 查看更多