2014届高三理科数学一轮复习试题选编8：三角函数的图象与性质（教师版）

2014届高三理科数学一轮复习试题选编8：三角函数的图象与性质（教师版）

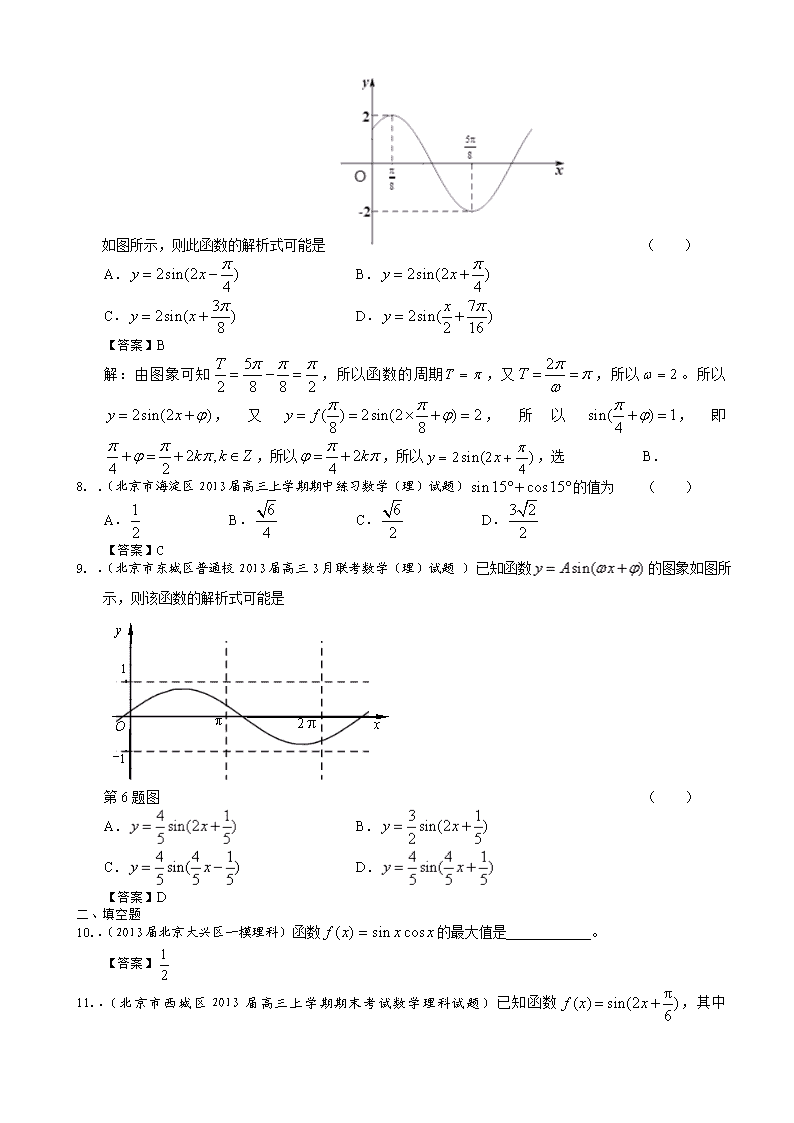
‎2014届高三理科数学一轮复习试题选编8：三角函数的图象与性质 一、选择题 ．（北京北师特学校203届高三第二次月考理科数学）把函数的图像上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,再把图像向左平移个单位,这时对应于这个图像的解析式是 （　　）‎ A． B． C．D．‎ ‎【答案】A【解析】把函数的图像上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,得到的图象,再把图像向左平移个单位,得到,所以选A． ‎ ．（北京市海淀区2013届高三5月查缺补漏数学（理））函数图象的两条相邻对称轴间的距离为 （　　）‎ A． B． C． D． ‎ ‎【答案】 B．‎ ．（2013届北京大兴区一模理科）函数 （　　）‎ A．在上递增 B．在上递增，在上递减 ‎ C．在上递减 D．在上递减，在上递增 ‎【答案】D ．（2013北京丰台二模数学理科试题及答案）下列四个函数中,最小正周期为,且图象关于直线对称的是 （　　）‎ A． B． ‎ C． D．‎ ‎【答案】 C．‎ ．（北京北师特学校203届高三第二次月考理科数学）函数的最小正周期等于 （　　）‎ A． B．‎2‎ C． D．‎ ‎【答案】A【解析】,所以函数的周期,选A． ‎ ．（2013北京高考数学（理））“φ=π”是“曲线y=sin(2x+φ)过坐标原点的” （　　）‎ A．充分而不必要条件 B．必要而不充分条件 ‎ C．充分必要条件 D．既不充分也不必要条件 ‎【答案】A 时,,过原点,便是函数过原点的时候可以取其他值,故选A答案. ‎ ．（北京市丰台区2013届高三上学期期末考试 数学理试题 ）函数 在一个周期内的图象如图所示，则此函数的解析式可能是 （　　）‎ A． B． ‎ C． D．‎ ‎【答案】B 解：由图象可知，所以函数的周期，又，所以。所以，又，所以，即，所以，所以，选 B．‎ ．（北京市海淀区2013届高三上学期期中练习数学（理）试题）的值为 （　　）‎ A． B． C． D．‎ ‎【答案】C ‎ ．（北京市东城区普通校2013届高三3月联考数学（理）试题 ）已知函数的图象如图所示，则该函数的解析式可能是 ‎ x y O ‎2‎ ‎1‎ ‎-1‎ 第6题图 （　　）‎ A． B．‎ C． D．‎ ‎【答案】D 二、填空题 ．（2013届北京大兴区一模理科）函数的最大值是 。‎ ‎【答案】 ‎ ．（北京市西城区2013届高三上学期期末考试数学理科试题）已知函数，其中．当 时，的值域是______；若的值域是，则的取值范围是______． ‎ ‎【答案】，‎ 解：若，则，，此时，即的值域是。‎ 若，则，。因为当或时，，所以要使的值域是，则有，即，所以，即的取值范围是。‎ ．（北京四中2013届高三上学期期中测验数学(理)试题）定义一种运算,令,且,‎ 则函数的最大值是______‎ ‎【答案】 【解析】令,则 ‎ ‎∴由运算定义可知, ‎ ‎∴当,即时,该函数取得最大值. 由图象变换可知, ‎ 所求函数的最大值与函数在区间上的最大值相同. ‎ ．（北京北师特学校203届高三第二次月考理科数学）把函数的图象沿 x轴向左平移个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数图象,对于函数有以下四个判断:‎ ‎①该函数的解析式为; ②该函数图象关于点对称; ③该函数在上是增函数;④函数在上的最小值为,则.‎ 其中,正确判断的序号是________________________‎ ‎【答案】②④【解析】将函数向左平移得到 ‎,然后纵坐标伸长到原来的2倍得到,即.所以①不正确.,所以函数图象关于点对称,所以②正确.由,得,即函数的单调增区间为,当时,增区间为,所以③不正确.,当时,,所以当时,函数值最小为,所以.所以④正确.所以正确的命题为②④. ‎ 三、解答题 ．（北京市朝阳区2013届高三第一次综合练习理科数学）已知函数()的最小正周期为.‎ ‎(Ⅰ)求的值及函数的单调递增区间;‎ ‎(Ⅱ)当时,求函数的取值范围.‎ ‎【答案】本小题满分13分) ‎ 解:(Ⅰ) ‎ ‎ ‎ ‎ ‎ 因为最小正周期为,所以 ‎ 所以. ‎ 由,,得. ‎ 所以函数的单调递增区间为[], ‎ ‎(Ⅱ)因为,所以, ‎ 所以 ‎ 所以函数在上的取值范围是[] ‎ ．（北京北师特学校203届高三第二次月考理科数学）已知函数.‎ ‎(I)求的最小正周期; (II)求在区间上的取值范围.‎ ‎【答案】解: ‎ ‎ ‎ ‎(1) ‎ ‎(2) ‎ ‎, ‎ ．（北京四中2013届高三上学期期中测验数学(理)试题）已知函数.‎ ‎(1)求函数图象的对称轴方程;‎ ‎(2)求的单调增区间.‎ ‎(3)当时,求函数的最大值,最小值.‎ ‎【答案】解: ‎ ‎(I) ‎ 令. ‎ ‎∴函数图象的对称轴方程是 ‎ ‎(II) ‎ ‎ ‎ 故的单调增区间为 ‎ ‎(III) , ‎ ‎ ‎ 当时,函数的最大值为1,最小值为 ‎ ．（北京市海淀区2013届高三5月查缺补漏数学（理））已知函数,且 ‎(Ⅰ)求的值.‎ ‎(Ⅱ)求函数在区间 上的最大和最小值.‎ ‎【答案】解:(I) ‎ ‎(II)因为 ‎ 设因为所以 ‎ 所以有 ‎ 由二次函数的性质知道,的对称轴为 ‎ 所以当 ,即,时,函数取得最小值 ‎ ‎ 当,即,时,函数取得最大小值 ‎ ．（北京市东城区2013届高三上学期期末考试数学理科试题）已知函数．‎ ‎（Ⅰ）求的最小正周期及单调递减区间；‎ ‎（Ⅱ）若在区间上的最大值与最小值的和为，求的值．‎ ‎【答案】解：（Ⅰ）‎ ‎.……………………………………………3分 所以．……………………………………………………………4分 由，‎ 得．‎ 故函数的单调递减区间是（）．…………………7分 ‎（Ⅱ）因为，‎ 所以．‎ 所以．…………………………………………………………10分 因为函数在上的最大值与最小值的和，‎ 所以．…………………………………………………………………………13分 ．（北京市顺义区2013届高三第一次统练数学理科试卷（解析））已知函数的最小正周期为.‎ ‎(I)求的值;‎ ‎(II)求函数在区间上的最大值和最小值.‎ ‎【答案】解:(I) ‎ ‎ ‎ ‎ ‎ ‎ ‎ 因为是最小正周期为, ‎ 所以, ‎ 因此 ‎ ‎(II)由(I)可知,, ‎ 因为, ‎ 所以 ‎ 于是当,即时,取得最大值; ‎ 当,即时,取得最小值 ‎ ．（北京市昌平区2013届高三上学期期末考试数学理试题 ）（本小题满分13分）已知函数.‎ ‎（Ⅰ）求的定义域及最小正周期； ‎ ‎（Ⅱ）求在区间上的最值.‎ ‎【答案】解：（Ⅰ）由得(Z)，‎ 故的定义域为RZ}．…………………2分 因为 ‎，………………………………6分 所以的最小正周期．…………………7分 ‎（II）由 …………..9分 当，…………….11分 当.……………….13分 ．（2013北京海淀二模数学理科试题及答案）已知函数.‎ ‎(Ⅰ)求函数的定义域;‎ ‎(Ⅱ) 求函数的单调递增区间.‎ ‎【答案】解:(I)因为所以 所以函数的定义域为 ‎ ‎(II)因为 ‎ 又的单调递增区间为 , ‎ 令 解得 又注意到 ‎ 所以的单调递增区间为, ‎ ．（北京市石景山区2013届高三上学期期末考试数学理试题 ）已知函数．‎ ‎（Ⅰ）求的定义域及最小正周期；‎ ‎（Ⅱ）求在区间上的最大值和最小值．‎ ‎【答案】（Ⅰ）因为，所以.‎ 所以函数的定义域为 ……………2分 ‎ ‎ ‎ ……………5分 ‎ ……………7分 ‎ ‎（Ⅱ）因为，所以 ……………9分 当时，即时，的最大值为； ……………11分 当时，即时，的最小值为. ………13分 ．（北京市海淀区2013届高三上学期期中练习数学（理）试题）已知函数.‎ ‎(Ⅰ)求的值;‎ ‎(Ⅱ)求函数的最小正周期及单调递减区间.‎ ‎【答案】解:(Ⅰ)因为 ‎ ‎ ‎ ‎ ‎ ‎ ‎ 所以 ‎ ‎(Ⅱ)因为 ‎ 所以 ‎ 又的单调递减区间为, ‎ 所以令 ‎ 解得 ‎ 所以函数的单调减区间为, ‎ ．（2013北京昌平二模数学理科试题及答案）已知函数.‎ ‎(Ⅰ)求;‎ ‎(Ⅱ)求的最小正周期及单调递增区间.‎ ‎【答案】解:(Ⅰ) ‎ ‎ ‎ ‎(Ⅱ)的最小正周期 ‎ 又由可得 ‎ 函数的单调递增区间为 ‎ ．（2013届北京市延庆县一模数学理）已知.‎ ‎（Ⅰ）求的最小正周期和单调递增区间；‎ ‎（Ⅱ）若，求的最小值及取得最小值时对应的的取值．‎ ‎【答案】解：（Ⅰ）‎ ‎ …………4分 ‎，最小正周期为. …………5分 由，得 …………6分 ‎ …………7分 ‎ …………8分 单调递增区间为. …………9分 ‎（Ⅱ）当时，， …………10分 在区间单调递增， …………11分 ‎，对应的的取值为. …………13分 ．（北京市东城区普通高中示范校2013届高三3月联考综合练习（二）数学（理）试题 ）(本小题满分13分) 已知函数 ‎ 其中 ,.‎ ‎（1）求函数的值域；‎ ‎（2）若函数的图象与直线的两个相邻交点间的距离为，求函数的单调增区间.‎ ‎【答案】解：（1） = …………………………………5分 所以函数的值域为 …………………………………………………7分 ‎（2）由 得 …………………………………………………9分 ‎ 所以 由 ………………………………………11分 得 ‎ 所以函数的单调增区间为. ………13分 ．（北京市海淀区北师特学校2013届高三第四次月考理科数学）已知，．‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）求函数的值域．‎ ‎【答案】解：（Ⅰ）因为，且，‎ 所以，．‎ 因为 ‎．‎ 所以． ……………………6分 ‎（Ⅱ）由（Ⅰ）可得．‎ 所以 ‎，．‎ 因为，所以，当时，取最大值；‎ 当时，取最小值．‎ 所以函数的值域为． ……………………13分 ．（北京市朝阳区2013届高三上学期期末考试数学理试题 ）（本小题满分13分）‎ 已知函数. ‎ ‎（Ⅰ）求函数的最小正周期及单调递减区间；‎ ‎（Ⅱ）求函数在上的最小值.‎ ‎【答案】解：（Ⅰ） ‎ ‎ …………………………………………2分 ‎ ‎ ……………………………………………4分 所以函数的最小正周期为. …………………………………………6分 由，，则.‎ 函数单调递减区间是，. ………………………9分 ‎(Ⅱ)由，得. ………………………………………11分 则当，即时，取得最小值. …………………13分 ．（2013届北京丰台区一模理科）已知函数 ‎（Ⅰ）求函数的最小正周期和单调递增区间；‎ ‎（Ⅱ）求函数在上的值域.‎ ‎【答案】解：（Ⅰ），…………………3分 最小正周期T=, …………………………………………………4分 单调增区间, …………………………………7分 ‎（Ⅱ），‎ ‎， ……………………………………………10分 在上的值域是. …………………………………13分 ．（2013北京顺义二模数学理科试题及答案）已知函数.‎ ‎(I)求的值;‎ ‎(II)求函数的最小正周期及单调递减区间.‎ ‎【答案】解:(I) ‎ ‎ ‎ ‎(II),得 ‎ 故的定义域为. ‎ 因为 ‎ ‎ ‎ ‎, ‎ 所以的最小正周期为. ‎ 因为函数的单调递减区间为, ‎ 由, ‎ 得, ‎ 所以的单调递减区间为 ‎ ．（2013届北京海滨一模理科）已知函数.‎ ‎（Ⅰ）求的值和的最小正周期；‎ ‎（Ⅱ）求函数在区间上的最大值和最小值.‎ ‎【答案】解：（I）因为 ‎………………2分 ‎………………4分 ‎………………6分所以………………7分 所以 的周期为………………9分 ‎（II）当时，，‎ 所以当时，函数取得最小值………………11分 当时，函数取得最大值………………13分 ．（北京市通州区2013届高三上学期期末考试理科数学试题 ）已知函数．‎ ‎（Ⅰ）求的最小正周期； ‎ ‎（Ⅱ）求函数在的最大值和最小值．‎ ‎【答案】解：（Ⅰ）由已知，得 ‎ ……………………2分 ‎， ……………………4分 所以　，‎ 即　　的最小正周期为； ……………………6分 ‎（Ⅱ）因为　，所以　． ……………… 7分 于是，当时，即时，取得最大值；…… 10分 当时，即时，取得最小值．……………13分 ．（2013届北京市高考压轴卷理科数学）已知向量,记函数.求:‎ ‎(I)函数的最小值及取得小值时的集合; ‎ ‎(II)函数的单调递增区间.‎ ‎【答案】解:(Ⅰ) ‎ ‎ ‎ ‎=, ‎ 当且仅当,即时,, ‎ 此时的集合是 ‎ ‎(Ⅱ)由,所以, ‎ 所以函数的单调递增区间为 ‎ ．（北京市东城区普通高中示范校2013届高三12月综合练习(一)数学理试题）已知函数 ‎(1)求函数的最小正周期和单调递增区间;‎ ‎(2)函数的图象经过怎样的变换可以得到的图象?‎ ‎【答案】解:(1) ‎ ‎= ‎ ‎= ‎ ‎= ‎ 最小正周期 ‎ 单调递增区间 , ‎ ‎(2) 向左平移个单位;向下平移个单位 ‎ ．（2013北京东城高三二模数学理科）已知函数. ‎ ‎(Ⅰ)求的最小正周期;‎ ‎(Ⅱ)当时,求的取值范围. ‎ ‎【答案】(共13分)解:(Ⅰ)因为 ‎ ‎= . ‎ 所以的最小正周期. ‎ ‎(Ⅱ) 因为,所以. ‎ 所以的取值范围是 ‎ ．（北京市朝阳区2013届高三上学期期中考试数学（理）试题）函数部分图象如图所示.‎ ‎(Ⅰ)求函数的解析式,并写出其单调递增区间;‎ ‎(Ⅱ)设函数,求函数在区间 ‎ 上的最大值和最小值.‎ ‎【答案】解:(Ⅰ)由图可得,, ‎ 所以,所以 ‎ 当时,,可得 , ‎ 因为,所以. ‎ 所以函数的解析式为. ‎ 函数的单调递增区间为 ‎ ‎(Ⅱ)因为 ‎ ‎ ‎ ‎ ‎ 因为,所以. ‎ 当,即时,函数有最大值为; ‎ 当,即时,函数有最小值 ‎ ．（2013届北京西城区一模理科）已知函数的一个零点是． ‎ ‎（Ⅰ）求实数的值； ‎ ‎（Ⅱ）设，求的单调递增区间． ‎ ‎【答案】（Ⅰ）解：依题意，得， ………………1分 即 ， ………………3分 解得 ． ………………5分 ‎（Ⅱ）解：由（Ⅰ）得 ． ………………6分 ‎ ………………7分 ‎ ………………8分 ‎ ………………9分 ‎． ………………10分 由 ，‎ 得 ，． ……………12分 所以 的单调递增区间为，． ……13分 ．（2013北京房山二模数学理科试题及答案）已知函数的最小正周期为,且图象过点.‎ ‎(Ⅰ)求的值;‎ ‎(Ⅱ)设,求函数的单调递增区间.‎ ‎【答案】(Ⅰ)由最小正周期为可知 , ‎ 由得 , ‎ 又, 所以 ,, ‎ ‎(Ⅱ)由(Ⅰ)知 ‎ 所以 ‎ 解得 ‎ 所以函数的单调增区间为 ‎ ．（2011年高考（北京理））已知函数 ‎(Ⅰ)求的最小正周期;‎ ‎(Ⅱ)求在区间上的最大值和最小值.‎ ‎【答案】【命题立意】本题考查了两角和差的三角函数公式和二倍角公式以及三角函数的图象和性质,会根据角的范围利用三角函数的图象求得三角函数的最值. ‎ ‎【解析】(Ⅰ)因为 ‎ ‎ ‎ 所以函数的最小正周期为 ‎ ‎(Ⅱ)因为,所以 ‎ 于是当,即时,取得最大值2; ‎ 当,即时,取得最小值-1 ‎