- 2021-02-26 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习函数的表示法课件(28张)(全国通用)
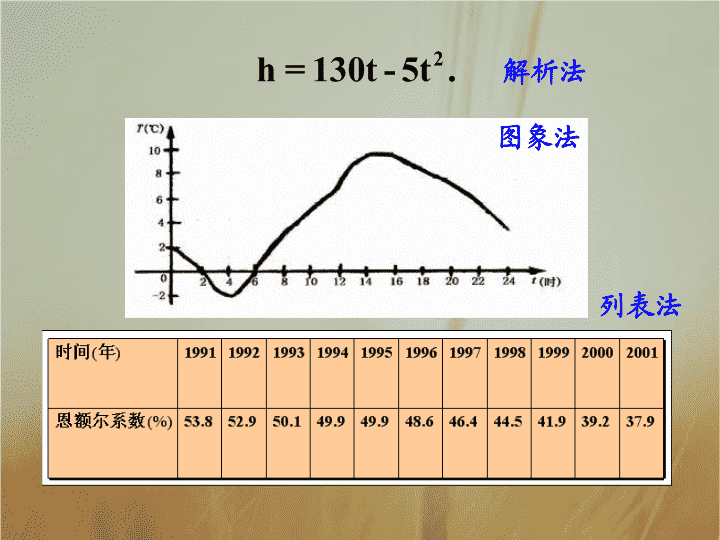
函数的表示法 解析法,列表法,图象法 . 回想函数的表示方法有哪几种? 用数学表达式表示两个变量之间的对应关系 列出表格来表示两个变量之间的对应关系 用图象表示两个变量之 间的对应关系 解析法 图象法 列表法 那么这三种表示方法各自有什么优点呢?面对实际问题时怎么样选用恰当方法来表示函数呢? 解:这个函数的定义域是数集{1,2,3,4,5}; 用解析法可将函数y=f(x)表示为 例 在礼品盒的专卖店里, 某种包装盒的单价是 3 元,买 x 个包装盒需要 y 元 , 试用函数的三种表示法表示函数 . 用解析法表示函数是否一定要写出自变量的取值范围? 用列表法可将函数表示为 : 笔记本数 x 1 2 3 4 5 钱数 y 3 6 9 12 15 函数的定义域是函数存在的前提,再写函数解析式的时候,一定要写出函数的定义域 . 用图象法可将函数表示为下图 : . . . . . 0 1 2 3 4 5 3 6 9 12 15 x y y 用描点法画函数图象的一般步骤是什么?本题中的图象为什么不是一条直线? 列表、描点、连线(视其定义域决定是否连线) . 函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等 . 思考 注意 是连续的直线,但 却是 5 个离散的点 . 所以说在函数概念中,对应关系,定义域,值域是一个整体 . 解析法 图象法 列表法 ① 函数关系清楚、精确; ② 容易从自变量的值求出其对应的函数值;③便于研究函数的性质 . 能形象直观的表示出函数的变化趋势,是今后利用数形结合思想解题的基础 . 不必通过计算就知道当自变量取某些值时函数的对应值,当自变量的值的个数较少时使用 . 三种表示方法的特点 解析法是中学研究函数的主要表达方法 . 列表法在实际生产和生活中有广泛的应用 . 所有的函数都能用解析法表示吗? 例 : 下表是某校高一( 1 )班三名同学在高一学年度六次数学测试的成绩及班级平均分表 . 第一次 第二次 第三次 第三次 第五次 第六次 王伟 98 87 91 92 88 95 张城 90 76 88 75 86 80 赵磊 68 65 73 72 75 82 班级平均分 88.2 78.3 85.4 80.3 75.7 82.6 对这三位同学在高一学年度的数学学习情况做一个分析 . 成绩 测试序号 姓名 解:从表中可以知道每位同学在每次测试中的成绩,但是不容易看出每位同学的成绩的变化情况 . 可以将 “ 成绩 ” 与 “ 测试序号 ” 之间的关系用函数图像表示出来,如图 1 ,那么就能比较直观地看到成绩变化的情况 . 1 3 2 4 x 0 5 6 60 y 70 80 90 100 王伟 张城 赵磊 班级平均分 图 1 1 3 2 4 x 0 5 6 60 y 70 80 90 100 王伟 张城 赵磊 班级平均分 图 2 为了更容易的看出学生的学习情况,将离散的点用虚线连接。 在图 2 中看到,王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且比较优秀 . 张诚同学的数学成绩不稳定,总是在班级平均水平上下波动,而且幅度较大 . 赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高 . 例 画出函数 y=|x| 的图象 . -2 -3 0 1 2 3 x y 1 2 3 4 5 -1 解: 图象如下: y= x, x ≥0 -x, x<0 变式 1 :作函数 y=|x - 1| 的图像 . y 2 3 4 5 -2 -3 0 1 2 3 x 1 -1 y=|x| y=|x - 1| 变式 2 :作函数 y=|x - 1| + 1 的图像 . -2 -3 1 2 3 x 0 y 1 2 3 4 -1 y=|x - 1| y=|x - 1| + 1 1. 有些函数在它的定义域中,对于自变量 x 的不同取值范围,对应关系不同,这种函数通常称为 分段函数 . 分段函数的表达式虽然不止一个,但它不是几个函数,而是一个函数 . 2. 函数图象不一定是光滑的曲线(直线),还可以是一些 孤立的点,一些线段,一段曲线 等 . 注意 函数是两个数集之间的一种确定关系,那么现在将数集扩展到任意集合,那又会得到什么呢? 思考 常见的对应关系: 1. 对于坐标平面内任何一个点 A ,都有唯一的有序实数对( x, y) 和它对应; 2. 某影院的某场电影的每一张电影票有唯一确定的座位与它对应; 3. 长途汽车上的每位乘客都有唯一确定的座位相对应; 4. 对于任何一个实数,数轴上都有唯一的点和它对应; 我们把它们称作什么呢? 称对应 f: A→B 为从集合 A 到集合 B 的一个 映射 . 函数是从非空数集 A 到非空数集 B 的映射 . 映射是从集合 A 到集合 B 的一种对应关系,这里的集合 A 、 B 可以是数集,也可以是其他集合 . 函数是一种特殊的映射 . 设 A,B 是两个非空的集合,如果按某一个确定的对应关系 f ,使对于集合 A 中的任意一个元素 x ,在集合 B 中都有惟一确定的元素 y 与之对应,那么就称对应 f:A→B 为从集合 A 到集合 B 的一个 映射 . 函数概念与映射概念之间有怎样的关系?有什么异同? 判断下面对应关系是不是映射? 9 4 1 3 -3 2 -2 1 -1 √ √ 1 2 3 4 5 6 1 2 3 9 4 1 3 -3 2 -2 1 -1 × √ B A 2 乘以 映射 f:A→B ,可理解为以下几点 : 2 、 A 中每个元素在 B 中必有惟一的元素和它对应 ; 3 、 A 中元素与 B 中元素的对应关系,可以是:一 对一,多对一,但不能一对多 . 1 、映射有三个要素:两个集合、一个对应法则, 三者缺一不可 ; 例 以下给出的对应是不是从集合 A 到 B 的映射? ( 1 )集合 A={P︱P 是数轴上的点 } ,集合 B=R ,对应关系 f :数轴上的点与它所代表的实数对应; ( 2 )集合 A={P︱P 是平面直角坐标系中的点 } ,集合 B={(x , y)︱ } ,对应关系 f :平面直角坐标系中的点与它的坐标对应; ( 3 )集合 A={x︱x 是三角形 } ,集合 B={x︱x 是圆 } ,对应关系 f :每一个三角形都对应它的内切圆; ( 4 )集合 A={x︱x 是新华中学班级 } ,集合 B={x︱x 是新华中学的学生 } ,对应关系 f :每一班级都对应班里的学生 . 解 :( 1 )按照建立数轴的方法可知,数轴上的任意一个点,都与唯一的实数与之对应,所以这个对应 f : A→B 是从集合 A 到 B 的一个映射 . ( 2 )按照建立平面直角坐标系的方法可知,平面直角坐标系中的任意一个点,都有唯一的一个实数对与之对应,所以这个对应 f : A→B 是从集合 A 到 B 的一个映射 . ( 3 )由于每一个三角形只有一个内切圆与之对应,所以这个对应 f : A→B 是从集合 A 到 B 的一个映 . ( 4 )新华中学的每一班级里的学生都不止一个,即与一个班级对应的学生不止一个,所以这个对应 f : A→B 不是从集合 A 到 B 的一个映射 . 对应关系 f 改为:每个学生都对应它的班级,那么 f : B→A 是集合从 B 到 A 的映射吗? ( 1 )理解函数的三种表示方法; ( 2 )在具体的实际问题中能够选用恰当的表 示法来表示函数; ( 3 )注意分段函数的表示方法及其图象的画法 ; ( 4 )映射的概念 . 课堂小结 1. 函数 若 f(x)=3, 则 x 的值 是 ( ) A. 1 B. 1 或 3/2 C. ± D. D 课堂练习 2 . 设 A={1,2,3} , B={3,4,5,6,7,8,9} ,集合 A 中的元素 x 按照对应法则“乘 2 加 1” 和集合 B 中的元素 2x+1 对应.这个对应是不是映射? 解:是 . 1 2 3 3 4 5 6 7 8 9 A B 2x+1查看更多