人教版高三数学总复习课时作业4

人教版高三数学总复习课时作业4

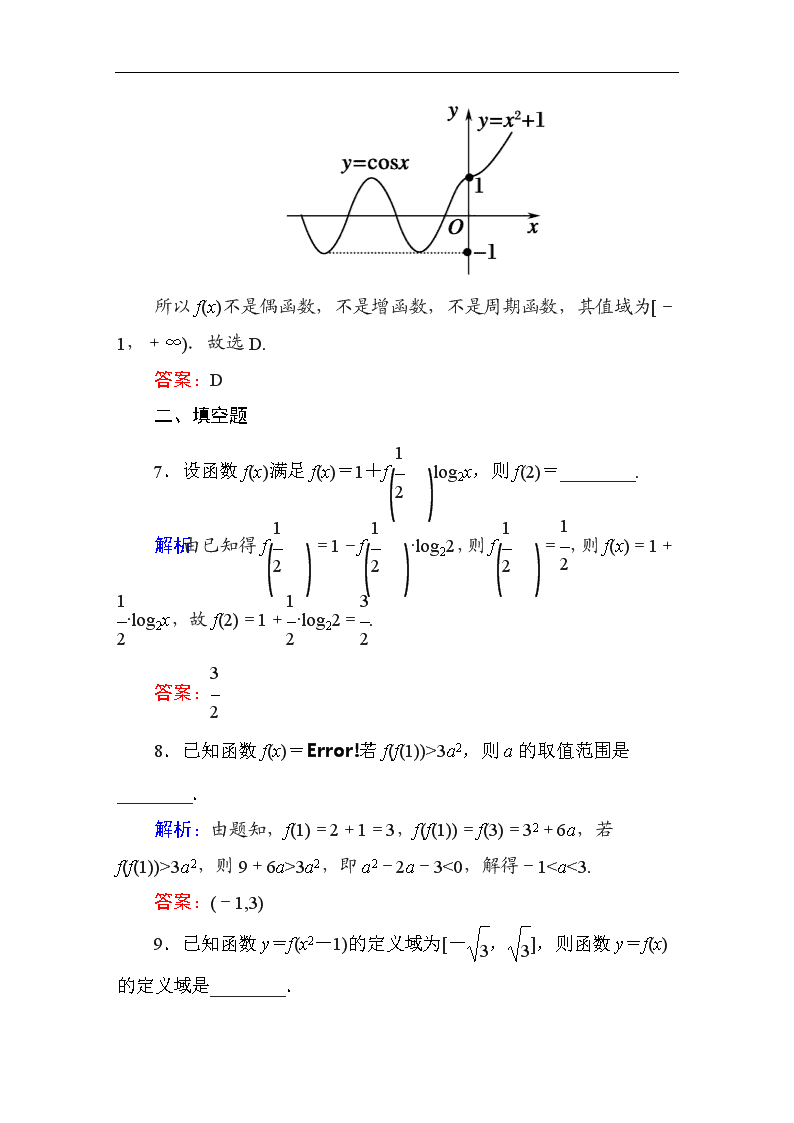
第二章　函数、导数及其应用 课时作业4　函数及其表示 一、选择题 ‎1．(2014·江西卷)函数f(x)＝ln(x2－x)的定义域为(　　)‎ A．(0,1)‎ B．[0,1]‎ C．(－∞，0)∪(1，＋∞)‎ D．(－∞，0]∪[1，＋∞)‎ 解析：由题意可知x2－x>0，解得x<0或x>1.‎ 故函数f(x)的定义域为(－∞，0)∪(1，＋∞)．‎ 答案：C ‎2．已知函数f(x)＝若f(f(1))＝4a，则实数a等于(　　)‎ A. B. C．2 D．4‎ 解析：∵f(1)＝2，∴f(f(1))＝f(2)＝4＋2a＝4a，解得a＝2.故选C.‎ 答案：C ‎3．设函数f(x)＝那么f(2 013)＝(　　)‎ A．27 B．9‎ C．3 D．1‎ 解析：根据题意，当x≥5时，f(x)＝f(x－5)，‎ ‎∴f(2 013)＝f(3)，而当0≤x<5时，f(x)＝x3，‎ ‎∴f(3)＝33＝27，故选A.‎ 答案：A ‎4．(2014·江西卷)已知函数f(x)＝5|x|，g(x)＝ax2－x(a∈R)，若f(g(1))＝1，则a＝(　　)‎ A．1 B．2‎ C．3 D．－1‎ 解析：由题意可知f(g(1))＝1＝50，得g(1)＝0，‎ 则a－1＝0，即a＝1.故选A.‎ 答案：A ‎5．若函数f(x)＝的定义域为R，则实数a的取值范围是(　　)‎ A．(－2,2)‎ B．(－∞，－2)∪(2，＋∞)‎ C．(－∞，－2]∪[2，＋∞)‎ D．[－2,2]‎ 解析：由题意知，对于任意x∈R，x2＋ax＋1≥0恒成立，则Δ＝a2－4×1×1＝a2－4≤0，解得－2≤a≤2，故选D.‎ 答案：D ‎6．(2014·福建卷)已知函数f(x)＝则下列结论正确的是(　　)‎ A．f(x)是偶函数 B．f(x)是增函数 C．f(x)是周期函数 D．f(x)的值域为[－1，＋∞)‎ 解析：由题意，可得函数图象如下：‎ 所以f(x)不是偶函数，不是增函数，不是周期函数，其值域为[－1，＋∞)．故选D.‎ 答案：D 二、填空题 ‎7．设函数f(x)满足f(x)＝1＋flog2x，则f(2)＝________.‎ 解析：由已知得f＝1－f·log22，则f＝，则f(x)＝1＋·log2x，故f(2)＝1＋·log22＝.‎ 答案： ‎8．已知函数f(x)＝若f(f(1))>3a2，则a的取值范围是________．‎ 解析：由题知，f(1)＝2＋1＝3，f(f(1))＝f(3)＝32＋6a，若f(f(1))>3a2，则9＋6a>3a2，即a2－2a－3<0，解得－12x＋5.‎ 解：(1)设二次函数f(x)＝ax2＋bx＋c(a≠0)．‎ ‎∵f(0)＝1，∴c＝1.‎ 把f(x)的表达式代入f(x＋1)－f(x)＝2x，有 a(x＋1)2＋b(x＋1)＋1－(ax2＋bx＋1)＝2x.‎ ‎∴2ax＋a＋b＝2x.∴a＝1，b＝－1.∴f(x)＝x2－x＋1.‎ ‎(2)由x2－x＋1>2x＋5，即x2－3x－4>0，‎ 解得x>4或x<－1.‎ 故原不等式解集为{x|x>4或x<－1}．‎ ‎11．运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100，单位：千米/小时)．假设汽油的价格是每升2元，而汽车每小时耗油升，司机的工资是每小时14元．‎ ‎(1)求这次行车总费用y关于x的表达式；‎ ‎(2)当x为何值时，这次行车的总费用最低，并求出最低费用的值．‎ 解：(1)行车所用时间为t＝(h)，‎ y＝×2×＋，x∈[50,100]．‎ 所以，这次行车总费用y关于x的表达式是 y＝＋x，x∈[50,100]．‎ ‎(2)y＝＋x≥26，‎ 当且仅当＝x，‎ 即x＝18时，上述不等式中等号成立．‎ 当x＝18时，这次行车的总费用最低，最低费用为26元．‎ ‎1．(2014·浙江卷)已知函数f(x)＝x3＋ax2＋bx＋c，且09‎ 解析：由f(－1)＝f(－2)＝f(－3)得 解得 所以f(x)＝x3＋6x2＋11x＋c，由0

查看更多