苏教版数学七年级上册教案《2-2 有理数与无理数》教案

苏教版数学七年级上册教案《2-2 有理数与无理数》教案

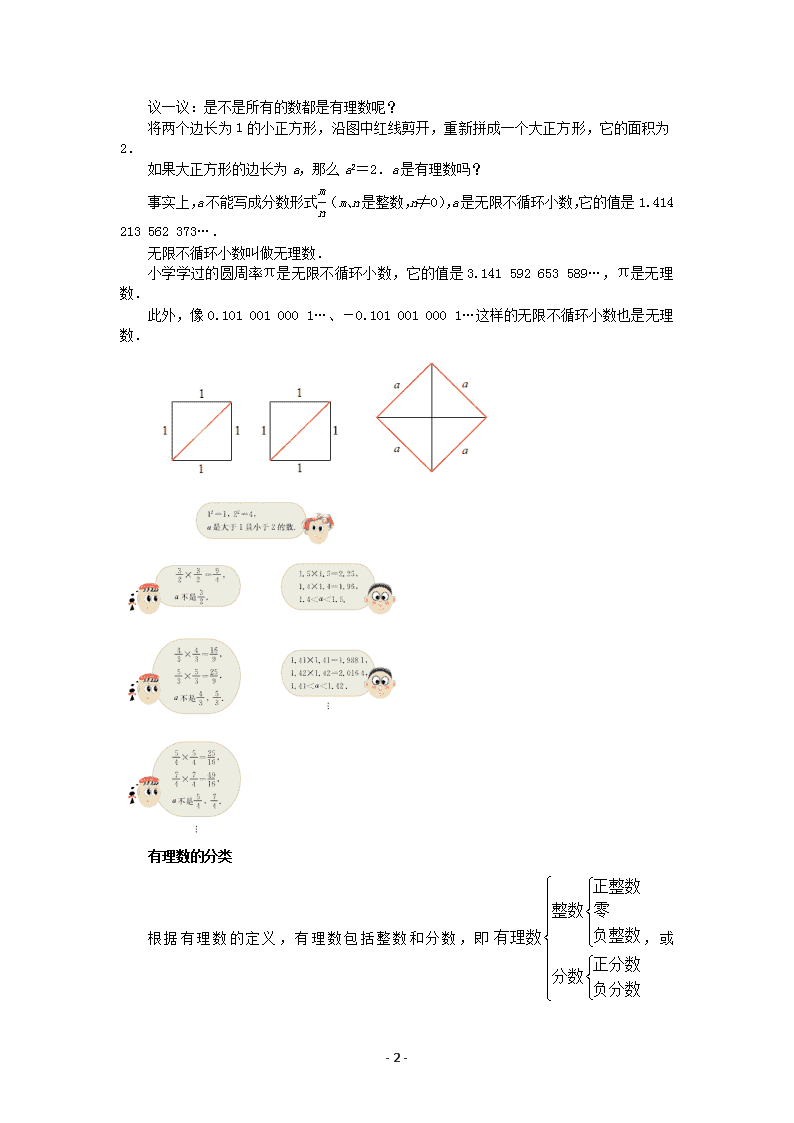
- 1 - 2.2 有理数与无理数 教学目标 1．理解有理数的意义和会对有理数进行分类； 2．了解无理数的意义. 教学重难点 【教学重点】 1．有理数的意义和分类； 2．无理数的意义． 【教学难点】 有理数的分类，区分有理数和无理数. 课前准备 课件. 教学过程 有理数 我们学过整数（正整数、负整数、零）和分数（正分数、负分数）．实际上，所有整数 都可以写成分母为 1 的分数的形式．如 55= ,1 44= ,1   00= .1 我们把能写成分数形式 m n （m、n 是整数，n≠0）的数叫做有理数． 想一想： 小学里学过的有限小数和无限循环小数是有理数吗？ 根据有理数的定义，有理数可以进行如下的分类：           正整数 整数 零 负整数有理数 正分数分数 负分数 ，或         正整数正有理数 正分数 有理数 零 负整数负有理数 负分数 结合 55= ,1 44= ,1   00= ,1 体会整数可化成分母为 1 的分数形式． 30.3 10  ， 3113.11 100    ， 10.333 3  ， 40.2666 15  ． 有限小数和无限循环小数都可以化为分数，它们都是有理数． 无理数 - 2 - 议一议：是不是所有的数都是有理数呢？ 将两个边长为 1 的小正方形，沿图中红线剪开，重新拼成一个大正方形，它的面积为 2． 如果大正方形的边长为 a，那么 a2＝2．a 是有理数吗？ 事实上，a 不能写成分数形式m n （m、n 是整数，n≠0），a 是无限不循环小数，它的值是 1.414 213 562 373…． 无限不循环小数叫做无理数． 小学学过的圆周率π是无限不循环小数，它的值是 3.141 592 653 589…，π是无理数． 此外，像 0.101 001 000 1…、－0.101 001 000 1…这样的无限不循环小数也是无理 数． 有理数的分类 根 据 有 理 数 的 定 义 ， 有 理 数 包 括 整 数 和 分 数 ， 即           正整数 整数 零 负整数有理数 正分数分数 负分数 ， 或 - 3 -          正整数正有理数 正分数 有理数 零 负整数负有理数 负分数 课堂练习： 将 下 列 各 数 填 入 相 应 括 号 内 ： 16 9.3 6  ， ， ，42 ， 0，-0.33 ， 0.333 ， 1.414 213 56 ，－2π， 3.303 003 000 3 ， -3.141 592 6 ． 正数集合：{ …}； 负数集合：{ …}； 正有理数集合：{ …}； 负有理数集合：{ …}． 正数集合：{9.3 ，42，0.333 ，1.414 213 56， 3.303 003 000 3 ，…}； 负数集合：{ 16 6  ， ，-0.33， 2π－ ，-3.141 592 6，…}； 正有理数集合：{9.3 ，42，0.333 ，1.414 213 56，…}； 负有理数集合：{ 16 6  ， ，-0.33，-3.141 592 6, …}． 课堂小结： 谈谈你这一节课有哪些收获． 回顾本节的教学内容，从知识和方法两个层面进行总结． 归纳知识体系，提炼思想和方法．