苏科版七年级上数学教学课件：有理数的加法与减法（1）

苏科版七年级上数学教学课件：有理数的加法与减法（1）

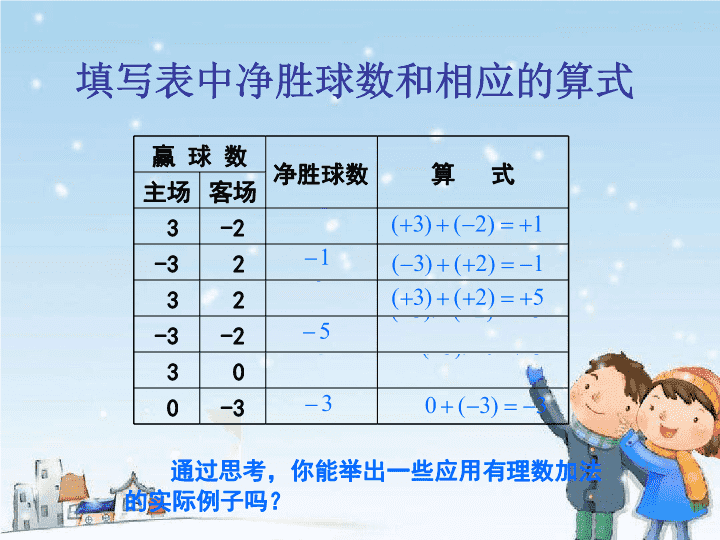
2.5 有理数的加法与减法（ 1 ） 创设情境 - 问题 　　甲、乙两队进行足球比赛．如果甲队在主场赢了 3 球，在客场输了 2 球，那么两场比赛后甲队净胜 1 球． 　　你能把上面比赛的过程及结果用有理数的算式表示出来吗？ 　　如果把赢球记为 “＋ ” ，输球记为 “－ ” ，可得算式： 填写表中净胜球数和相应的算式 赢 球 数 净胜球数 算 式 主场 客场 3 -2 -3 2 3 2 -3 -2 3 0 0 -3 通过思考，你能举出一些应用有理数加法的实际例子吗？ 数学实验室 1 ． 把笔尖放在数轴的原点，沿数轴先向左移动 5 个单位长度，再向右移动 3 个单位长度，这时笔尖停在“－ 2” 的位置上，请用数轴和算式分别表示以上过程及结果． 数学实验室 2 ． 把笔尖放在数轴的原点，沿数轴先向右移动 3 个单位长度再向左移动 2 个单位长度，这时笔尖停在“ 1” 的位置上． 请用数轴和算式分别表示以上过程及结果． 数学实验室 3 ．把笔尖放在数轴的原点，沿数轴先向左移动 3 个单位长度，再向左移动 2 个单位长度，这时笔尖的位置表示什么数，请用数轴和算式分别表示以上过程及结果 ． 数学实验室 仿照上面的做法，请在数轴上呈现下面的算式所表示的笔尖运动的过程和结果． （＋ 3 ）＋（＋ 3 ）＝ （＋ 3 ）＋（－ 5 ）＝ （＋ 4 ）＋（－ 4 ）＝ （－ 5 ）＋ 0 ＝ 探究归纳 任意两个有理数相加，和是多少？ 你能找到有理数相加的一般方法吗？ 议一议 （＋ 3 ）＋（＋ 2 ）＝ ＋ 5 （－ 1 ）＋（－ 2 ）＝ － 3 （＋ 3 ）＋（－ 2 ）＝ ＋ 1 （＋ 3 ）＋（－ 5 ）＝ － 2 （－ 4 ）＋（＋ 4 ）＝ 0 0 ＋（－ 3 ）＝ － 3 探究归纳 同号相加 异号相加 一个数与０相加 从加数的符号入手， 有理数加法可以分成三种情况． 探究归纳 和的符号与两个加数的符号一致， 和的绝对值等于两个加数绝对值之和． 从符号与绝对值两方面观察“和”与“两个加数”的联系． 同号相加 探究归纳 　　 在加数为异号时，和可能为正数、负数或零，观察“和”与“两个加数”在符号、绝对值上的关系． 　　 当两个加数绝对值不等时，和的符号与绝对值较大的加数的符号相同，和的绝对值等于加数中较大的绝对值减去较小的绝对值． 　　 当两个加数绝对值相等时，两个加数互为相反数，和为零． 异 号 相 加 探究归纳 　　一个数同零相加，仍得这个数 ． 探索总结 有理数加法法则： (1) 同号两数相加，取相同的符号，并把绝对值相加； (2) 异号两数相加，绝对值相等时，和为 0 ；绝对值不等时，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值； (3) 一个数与 0 相加，仍得这个数 ． 小试牛刀 解：原式 =+ （ 8+5 ） =+13 解：原式 =- （ 8+5 ） =-13 解：原式 =+ （ 8-5 ） =+3 解：原式 =- （ 8-5 ） =-3 解：原式 =0 解：原式 =+8 例 1 计算 （ 1 ）（＋ 8 ）＋ ( ＋ 5) （ 2 ）（－ 8) ＋ ( － 5) （ 3 ）（＋ 8) ＋ ( － 5) （ 4 ） ( － 8) ＋ ( ＋ 5) （ 5 ） ( － 8) ＋ ( ＋ 8) （ 6 ） ( ＋ 8) ＋ 0 ； 做一做 计算 （ 1 ）（ +10 ） + （ -4 ） ; （ 2 ）（ -15 ） + （ -32 ） ; （ 3 ）（ -9 ） + 0; （ 4 ） 43+ （ -34 ） ; （ 5 ）（ -10.5 ） + （ +1.3 ） ; （ 6 ）（ -1/2 ） +1/3. 请同学们再来试一试，完成下列填空 ： ( ＋ 5) ＋ ( － 3) ＝ ( 　 ) ； ( ＋ 4) ＋ ( － 10) ＝ ( 　 ) ； ( － 3) ＋ ( ＋ 8) ＝ ( 　 ) ； ( － 8) ＋ 3 ＝ ( 　 ) ． ＋ 2 － 6 ＋ 5 － 5 实践应用 － 160 － 18 0 － 2 例 2 　计算并注明相应的运算法则： 例 3 某公司三年的盈利情况如下表所示，规定盈利为 “ +” （单位：万元） （ 1 ）该公司前两年盈利了多少万元？ （ 2 ）该公司三年共盈利多少万元？ 第一年 第二年 第三年 -24 +15.6 +42 -24+15.6=-8.4 -24+15.6+42 =-8.4+42 =33.6 试一试 × √ 例 3 判断 （ 1 ）两个有理数相加，和一定比加数大 . （ ） （ 2 ）绝对值相等的两个数的和为 0. （ ） （ 3 ）若两个有理数的和为负数，则这两个数中 至少有一个是负数 . ( ) × 练一练： 1. 计算 ： （ 1 ） （ 2 ） （ 3 ） （ 4 ） 练一练： 2. 某仓库原有粮食 80 吨，第一天运进粮食 54 吨，第二天又运出粮食 32 吨，现在仓库共有粮食多少吨？ 3. 一个正数与一个负数的和是（ ） A 、正数 B 、负数 C 、零 D 、以上三种情况都有可能 4. 两个有理数的和（ ） A 、一定大于其中的一个加数 B 、一定小于其中的一个加数 C 、大小由两个加数符号决定 D 、大小由两个加数的符号及绝对值而决定 D D 80+54+(-32)=102 小学的加法是 有理数加法中的一种特例 ，即两个正数相加或正数与 0 相加 ． 与小学不同的是，有理数由符号与绝对值两部分组成，运算时 既要考虑符号，也要考虑绝对值． 小　结 （ 1 ）分类型；（ 2 ）确定和的符号； （ 3 ）确定和的绝对值． 2 ．有理数加法运算的 一般步骤 ： 1 ．有理数的加法与小学学的加法有什么 联系与区别？