初中数学中考复习课件章节考点专题突破：第五章 图形的性质(一)自我测试

初中数学中考复习课件章节考点专题突破：第五章 图形的性质(一)自我测试

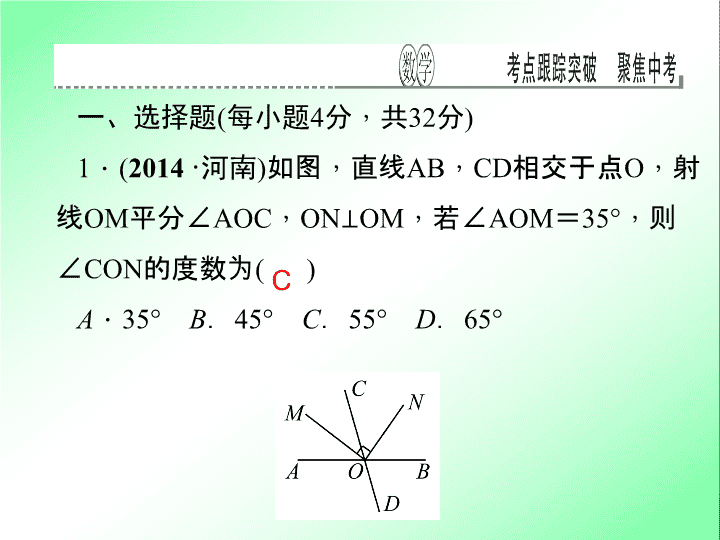
第五章　图形的性质 ( 一 ) 自我测试 一、选择题 ( 每小题 4 分 ， 共 32 分 ) 1 ． ( 2014 · 河南 ) 如图 ， 直线 AB ， CD 相交于点 O ， 射线 OM 平分 ∠ AOC ， ON ⊥ OM ， 若 ∠ AOM ＝ 35° ， 则 ∠ CON 的度数为 ( ) A ． 35° B ． 45° C ． 55° D ． 65° C 2 ． ( 2014 · 河北 ) 如图 ， 平面上直线 a ， b 分别过线段 OK 两端点 ( 数据如图 ) ， 则 a ， b 相交所成的锐角是 ( ) A ． 20° B ． 30° C ． 70° D ． 80° B 3 ． ( 2014· 达州 ) 如图 ， 在四边形 ABCD 中 ， ∠ A ＋ ∠ D ＝ α ， ∠ ABC 的平分线与 ∠ BCD 的平分线交于点 P ， 则 ∠ P ＝ ( ) A ． 90 ° － 1 2 α B ． 90 ° ＋ 1 2 α C . 1 2 α D ． 360 ° － α C 4 ． ( 2014 · 黄石 ) 以下命题是真命题的是 ( ) A ． 梯形是轴对称图形 B ． 对角线相等的四边形是矩形 C ． 四边相等的四边形是正方形 D ． 菱形有两条相互垂直的对称轴 D 5 ． ( 2013 · 安顺 ) 如图 ， 有两棵树 ， 一棵高 10 米 ， 另一棵高 4 米 ， 两树相距 8 米 ， 一只鸟从一棵树的树梢飞到另一棵树的树梢 ， 问小鸟至少飞行 ( ) A ． 8 米 B ． 10 米 C ． 12 米 D ． 14 米 B 6 ． ( 2014· 十堰 ) 如图 ， 在四边形 ABCD 中 ， AD ∥ BC ， DE ⊥ BC ， 垂足为点 E ， 连接 AC 交 DE 于点 F ， 点 G 为 AF 的中点 ， ∠ ACD ＝ 2 ∠ ACB. 若 DG ＝ 3 ， EC ＝ 1 ， 则 DE 的 长为 ( ) A ． 2 3 B . 10 C ． 2 2 D . 6 C 7 ． ( 2013· 深圳 ) 如图 ， 有一张一个角为 30° ， 最小边长为 2 的直角三角形纸片 ， 沿图中所示的中位线剪开后 ， 将两部 分拼成一个四边形 ， 所得四边形的周长是 ( ) A ． 8 或 2 3 B ． 10 或 4 ＋ 2 3 C ． 10 或 2 3 D ． 8 或 4 ＋ 2 3 D 8 ． ( 2014 · 黑龙江 ) 如图 ， 正方形 ABCD 中 ， AB ＝ 6 ， 点 E 在边 CD 上 ， 且 CD ＝ 3 DE . 将 △ ADE 沿 AE 对折至 △ AFE ， 延长 EF 交边 BC 于点 G ， 连接 AG ， CF . 则下列结论： ①△ ABG ≌△ AFG ； ② BG ＝ CG ； ③ AG ∥ CF ； ④ S △ EGC ＝ S △ AFE ； ⑤∠ AGB ＋ ∠ AED ＝ 145°. 其中正确的个数有 ( ) A ． 2 个 B ． 3 个 C ． 4 个 D ． 5 个 C 二、填空题 ( 每小题 6 分 ， 共 24 分 ) 9 ． ( 2014 · 广州 ) 已知 OC 是 ∠ AOB 的平分线 ， 点 P 在 OC 上 ， PD ⊥ OA ， PE ⊥ OB ， 垂足分别为点 D ， E ， PD ＝ 10 ， 则 PE 的长度为 ____ ． 10 10 ． ( 2014· 苏州 ) 如图 ， 在矩形 ABCD 中 ， AB BC ＝ 3 5 ， 以点 B 为圆心 ， BC 长为半径画弧 ， 交边 AD 于点 E. 若 AE·ED ＝ 4 3 ， 则矩形 ABCD 的面积为 __ __ ． 5 11 ． ( 2014 · 十堰 ) 如图 ， 在 △ ABC 中 ， 点 D 是 BC 的中点 ， 点 E ， F 分别在线段 AD 及其延长线上 ， 且 DE ＝ DF. 给出下列条件： ① BE ⊥ EC ； ② BF ∥ CE ； ③ AB ＝ AC. 从中选择一个条件使四边形 BECF 是菱形 ， 你认为这个条件是 ____ ． ( 只填写序号 ) ③ 12 ． ( 2014 · 陕西 ) 如图 ， 在正方形 ABCD 中 ， AD ＝ 1 ， 将 △ ABD 绕点 B 顺时针旋转 45° 得到 △ A′BD′ ， 此时 A′D′ 与 CD 交于点 E ， 则 DE 的长度为 ． 三、解答题 ( 共 44 分 ) 13 ． (8 分 ) ( 2013 · 湖州 ) 如图 ， 在 ▱ ABCD 中 ， E 是 CA 延长线上的点 ， F 是 AC 延长线上的点 ， 且 AE ＝ CF. 求证： (1) △ ABE ≌△ CDF ； (2)BE ∥ DF. 解： (1) ∵ 四边形 ABCD 是平行四边形 ， ∴ AB ∥ CD ， AB ＝ CD ， ∴∠ BAC ＝ ∠ DCA ， ∵∠ BAC ＋ ∠ BAE ＝ ∠ DCA ＋ ∠ DCF ＝ 180° ， ∴∠ BAE ＝ ∠ DCF ， ∵ AE ＝ CF ， ∴△ ABE ≌△ CDF (2) ∵△ ABE ≌△ CDF ， ∴∠ E ＝ ∠ F ， ∴ BE ∥ DF 14 ． (8 分 ) ( 2014 · 泰州 ) 如图 ， BD 是 △ ABC 的角平分线 ， 点 E ， F 分别在 BC ， AB 上 ， 且 DE ∥ AB ， EF ∥ AC. (1) 求证： BE ＝ AF ； 解： (1) ∵ DE ∥ AB ， EF ∥ AC ， ∴ 四边形 ADEF 是平行四边形 ， ∠ ABD ＝ ∠ BDE ， ∴ AF ＝ DE ， ∵ BD 是 △ ABC 的角平分线 ， ∴∠ ABD ＝ ∠ DBE ， ∴∠ DBE ＝ ∠ BDE ， ∴ BE ＝ DE ， ∴ BE ＝ AF (2) 若 ∠ ABC ＝ 60° ， BD ＝ 6 ， 求四边形 ADEF 的面积． 15 ． (8 分 ) ( 2013 · 荆门 ) 如图 ① ， 在 △ ABC 中 ， AB ＝ AC ， 点 D 是 BC 的中点 ， 点 E 在 AD 上． (1) 求证： BE ＝ CE ； (2) 如图 ② ， 若 BE 的延长线交 AC 于点 F ， 且 BF ⊥ AC ， 垂足为点 F ， ∠ BAC ＝ 45° ， 原题设其他条件不变．求证： △ AEF ≌△ BCF. 解： (1) ∵ AB ＝ AC ， D 是 BC 的中点 ， ∴∠ BAE ＝ ∠ EAC ， 在 △ ABE 和 △ ACE 中 ， ∵ AB ＝ AC ， ∠ BAE ＝ ∠ EAC ， AE ＝ AE ， ∴△ ABE ≌△ ACE ， ∴ BE ＝ CE 　 (2) ∵∠ BAC ＝ 45° ， BF ⊥ AF ， ∴△ ABF 为等腰直角三角形 ， ∴ AF ＝ BF ， 由 (1) 知 AD ⊥ BC ， ∴∠ EAF ＝ ∠ CBF ， 在 △ AEF 和 △ BCF 中 ， AF ＝ BF ， ∠ AFE ＝ ∠ BFC ＝ 90° ， ∠ EAF ＝ ∠ CBF ， ∴△ AEF ≌△ BCF 16 ． (10 分 ) ( 2013 · 黔东南州 ) 如图 ， 在正方形 ABCD 中 ， 点 M 是对角线 BD 上的一点 ， 过点 M 作 ME ∥ CD 交 BC 于点 E ， 作 MF ∥ BC 交 CD 于点 F. 求证： AM ＝ EF. 解： 过 M 点作 MQ ⊥ AD ， 垂足为点 Q ， 作 MP ⊥ AB ， 垂足为点 P ， ∵ 四边形 ABCD 是正方形 ， ∴ 四边形 MFDQ 和四边形 PBEM 是正方 形 ， 四边形 APMQ 是矩形 ， ∴ AP ＝ QM ＝ DF ＝ MF ， PM ＝ PB ＝ ME ， ∵ 在 △ APM 和 △ FME 中 ， î ï í ï ì AP ＝ MF ， ∠ APM ＝ ∠ FME ， PM ＝ ME ， ∴△ APM ≌△ FME ( SAS ) ， ∴ AM ＝ EF 17 ． (10 分 ) ( 2014 · 河南 ) 如图 ， CD 是 ⊙ O 的直径 ， 且 CD ＝ 2 cm ， 点 P 为 CD 的延长线上一点 ， 过点 P 作 ⊙ O 的切线 PA ， PB ， 切点分别为点 A ， B. (1) 连接 AC ， 若 ∠ APO ＝ 30° ， 试证明 △ ACP 是等腰三角形； (2) 填空： ① 当 DP ＝ ____ cm 时 ， 四边形 AOBD 是菱形； ②当 DP ＝ cm 时 ， 四边形 AOBP 是正方形 1