2020届高考数学大二轮复习 第1部分 专题1 集合、常用逻辑用语等 第3讲 不等式及线性规划练习
第一部分 专题一 第三讲 不等式及线性规划
A组
1.若a>b>0,c
B.<
C.> D.<
[解析] 令a=3,b=2,c=-3,d=-2,
则=-1,=-1,
所以A,B错误;
=-,=-,
所以<,
所以C错误.故选D.
2.下列不等式一定成立的是( C )
A.lg(x2+)>lgx(x>0)
B.sinx+≥2(x≠kπ,k∈Z)
C.x2+1≥2|x|(x∈R)
D.>1(x∈R)
[解析] 应用基本不等式:x,y>0,≥(当且仅当x=y时取等号)逐个分析,注意基本不等式的应用条件及取等号的条件.
当x>0时,x2+≥2·x·=x,
所以lg(x2+)≥lgx(x>0),故选项A不正确;
运用基本不等式时需保证一正二定三相等,
而当x≠kπ,k∈Z时,sinx的正负不定,故选项B不正确;
由基本不等式可知,选项C正确;
当x=0时,有=1,故选项D不正确.
3.关于x的不等式x2-2ax-8a2<0(a>0)的解集为(x1,
11
x2),且x2-x1=15,则a等于( A )
A. B.
C. D.
[解析] 由x2-2ax-8a2<0,得(x+2a)(x-4a)<0,因a>0,所以不等式的解集为(-2a,4a),即x2=4a,x1=-2a,由x2-x1=15,得4a-(-2a)=15,解得a=.
4.(2017·长春一模)已知一元二次不等式f(x)<0的解集为{x|x<-1或x>},则f(ex)>0的解集为( D )
A.{x|x<-1或x>-ln3}
B.{x|-1-ln3}
C.{x|x>-ln3}
D.{x|x<-ln3}
[解析] f(x)>0的解集为{x|-10得-10的解集为{x|x<-ln3}.
5.若变量x,y满足则x2+y2的最大值是( C )
A.4 B.9
C.10 D.12
[解析] 作出不等式组所表示的平面区域如图中阴影部分所示,设P(x,y)为平面区域内任意一点,则x2+y2表示|OP|2.显然,当点P与点A重合时,|OP|2取得最大值.由,解得,故A(3,-1).所以x2+y2的最大值为32+(-1)2=10.故选C.
6.(文)若实数x、y满足不等式组则w=的取值范围是( D )
A.[-1,] B.[-,]
C.[-,+∞) D.[-,1)
11
[解析] 作出不等式组表示的平面区域如图所示.据题意,即求点M(x,y)与点P(-1,1)连线斜率的取值范围.
由图可知wmin==-,wmax<1,
∴w∈[-,1).
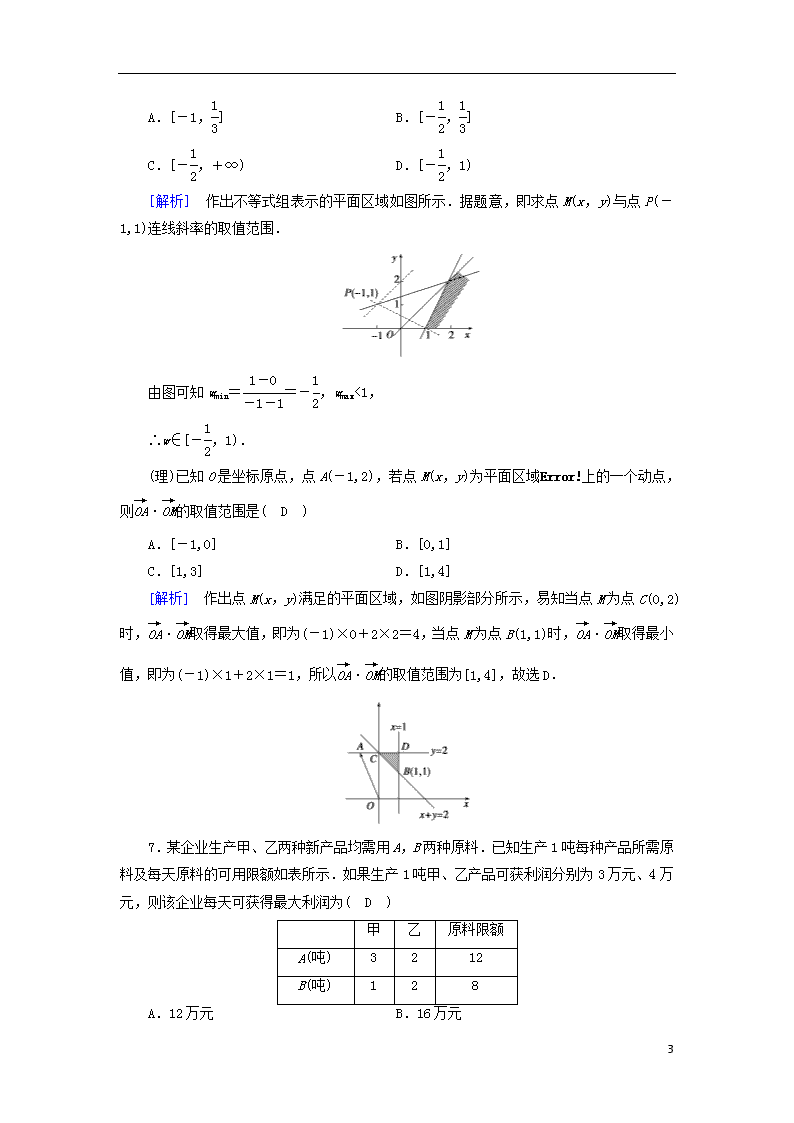
(理)已知O是坐标原点,点A(-1,2),若点M(x,y)为平面区域上的一个动点,则·的取值范围是( D )
A.[-1,0] B.[0,1]
C.[1,3] D.[1,4]
[解析] 作出点M(x,y)满足的平面区域,如图阴影部分所示,易知当点M为点C(0,2)时,·取得最大值,即为(-1)×0+2×2=4,当点M为点B(1,1)时,·取得最小值,即为(-1)×1+2×1=1,所以·的取值范围为[1,4],故选D.
7.某企业生产甲、乙两种新产品均需用A,B两种原料.已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( D )
甲
乙
原料限额
A(吨)
3
2
12
B(吨)
1
2
8
A.12万元 B.16万元
C.17万元 D.18万元
[解析] 设企业每天生产甲产品x吨、乙产品y吨,每天获得的利润为z万元,则有z=3x+4y,由题意得x,y满足:不等式组表示的可行域是以O(0,0),
11
A(4,0),B(2,3),C(0,4)为顶点的四边形及其内部.根据线性规划的有关知识,知当直线3x+4y-z=0过点B(2,3)时,z取最大值18,故该企业每天可获得最大利润为18万元.
8.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数a满足f(log2a)+f(loga)≤2f(1),则a的取值范围是( C )
A.[1,2] B.(0,]
C.[,2] D.(0,2]
[解析] 因为loga=-log2a,所以f(log2a)+f(loga)=f(log2a)+f(-log2a)=2f(log2a),原不等式变为2f(log2a)≤2f(1),即f(log2a)≤f(1),又因为f(x)是定义在R上的偶函数,且在[0,+∞)上递增,所以|log2a|≤1,即-1≤log2a≤1,解得≤a≤2,故选C.
9.已知a>0,x,y满足约束条件若z=2x+y的最小值为1,则a=( B )
A. B.
C.1 D.2
[解析] 画出可行域,如图所示,
由
得A(1,-2a),则直线y=z-2x过点A(1,-2a)时,z=2x+y取最小值1,故2×1-2a=1,解得a=.
10.已知x∈(0,+∞)时,不等式9x-m·3x+m+1>0恒成立,则m的取值范围是( C )
A.2-21),则由已知得函数f(t)=t2-mt+m+1的图象在t∈(1,+∞)上恒在x轴的上方,
则对于方程f(t)=0,有Δ=(-m)2-4(m+1)<0或
解得m<2+2.
11
11.已知AC,BD为圆O:x2+y2=4的两条互相垂直的弦,且垂足为M(1,),则四边形ABCD面积的最大值为( A )
A.5 B.10
C.15 D.20
[解析] 如图,作OP⊥AC于P,OQ⊥BD于Q,则OP2+OQ2=OM2=3,∴AC2+BD2=4(4-OP2)+4(4-OQ2)=20.又AC2+BD2≥2AC·BD,则AC·BD≤10,
∴S四边形ABCD=AC·BD≤×10=5,
当且仅当AC=BD=时等号成立.
12.函数f(x)=若f(x0)≤,则x0的取值范围是( C )
A.(log2,) B.(0,log2]∪[,+∞)
C.[0,log2]∪[,2] D.(log2,1)∪[,2]
[解析] ①当0≤x0<1时,2x0≤,x0≤log2,
∴0≤x0≤log2.
②当1≤x0≤2时,4-2x0≤,x0≥,
∴≤x0≤2,故选C.
13.(2018·衡水中学高三调研)已知f(x)是R上的减函数,A(3,-1),B(0,1)是其图象上两点,则不等式|f(1+lnx)|<1的解集是(,e2).
[解析] ∵|f(1+lnx)|<1,∴-10,则+的最小值为+.
[解析] ∵点A(1,1)在直线2mx+ny-2=0上,
∴2m+n=2,
∵+=(+)=(2+++1)≥(3+2=+,
当且仅当=,即n=m时取等号,
∴+的最小值为+.
16.已知函数f(x)=若对任意的x∈R,不等式f(x)≤m2-m恒成立,则实数m的取值范围是(-∞,-)∪[1,+∞).
[解析] 对于函数
f(x)=
当x≤1时,f(x)=-(x-)2+≤;
当x>1时,f(x)=logx<0.
则函数f(x)的最大值为.
则要使不等式f(x)≤m2-m恒成立,
则m2-m≥恒成立,即m≤-或m≥1.
B组
1.(2018·山东菏泽一模)已知直线ax+by+c-1=0(b,c>0)经过圆x2+y2-2y-5=0的圆心,则+的最小值是( A )
A.9 B.8
C.4 D.2
11
[解析] 圆x2+y2-2y-5=0化成标准方程,得x2+(y-1)2=6,
所以圆心为C(0,1).
因为直线ax+by+c-1=0经过圆心C,
所以a×0+b×1+c-1=0,即b+c=1.
因此+=(b+c)(+)=++5.
因为b,c>0,
所以+≥2=4.
当且仅当=时等号成立.
由此可得b=2c,且b+c=1,即b=,
c=时,+取得最小值9.
2.(2018·天津二模)已知函数f(x)=,则不等式f(1-x2)>f(2x)的解集是( D )
A.{x|-1-1+}
C.{x|-1--1}
[解析] 由f(x)=可得当x≤1时,函数f(x)为减函数,则由f(1-x2)>f(2x)可得或解得x<-1-或-1,所以不等式f(1-x2)>f(2x)的解集是{x|x<-1-或x>-1}.
3.已知x,y满足约束条件 若z=ax+y的最大值为4,则a=( B )
A. 3 B. 2
C. -2 D. -3
[解析] 由约束条件可画可行域如图,解得A(2,0),B(1,1).若过点A(2,0)时取最大值4,则a=2,验证符合条件;若过点B(1,1)时取最大值4,则a=3,而若a=3,则z=3x+y最大值为6(此时A(2,0)是最大值点),不符合题意. (也可直接代入排除)
4.(2018·德州模拟)若a=,b=,c=,则( C )
11
A.a1,所以b>a,
===log2532>1,
所以a>c,
故b>a>c.
5.已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得=4a1,则+的最小值为( A )
A. B.
C. D.不存在
[解析] 由an>0,a7=a6+2a5,设{an}的公比为q,
则a6q=a6+,所以q2-q-2=0.
因为q>0,所以q=2,
因为=4a1,所以a·qm+n-2=16a,
所以m+n-2=4,
所以m+n=6,
所以+=(m+n)(+)=(5++)≥(5+2)=,等号在=,即n=2m=4时成立.
6.若变量x,y满足则点P(2x-y,x+y)表示区域的面积为( D )
A. B.
C. D.1
[解析] 令2x-y=a,x+y=b,
解得
代入x,y的关系式得
画出不等式组表示的平面区域如图.
11
易得阴影区域面积S=×2×1=1.
7.(2018·临沂模拟)若不等式组表示的平面区域是一个三角形,则a的取值范围是( D )
A.[,+∞) B.(0,1]
C.[1,) D.(0,1]∪[,+∞)
[解析] 不等式组表示区域如图.
由图可知,0},则f(10x)>0的解集为{x|x<-lg_2}.
[解析] 由题意知,一元二次不等式f(x)<0的解集为{x|x<-1或x>},因为f(10x)>0,所以-1<10x<,即x0时,f(x)=x+≥2,若f(0)是f(x)的最小值,则f(0)=a≤2.
11.已知f(x)是定义在[-1,1]上的奇函数且f(1)=2,当x1、x2∈[-1,1],且x1+x2≠0时,有>0,若f(x)≥m2-2am-5对所有x∈[-1,1]、a∈[-1,1]恒成立,则实数m的取值范围是[-1,1].
[解析] ∵f(x)是定义在[-1,1]上的奇函数,
∴当x1、x2∈[-1,1]且x1+x2≠0时,
>0等价于>0,
∴f(x)在[-1,1]上单调递增.
∵f(1)=2,∴f(x)min=f(-1)=-f(1)=-2.
要使f(x)≥m2-2am-5对所有x∈[-1,1],a∈[-1,1]恒成立,
即-2≥m2-2am-5对所有a∈[-1,1]恒成立,
∴m2-2am-3≤0,设g(a)=m2-2am-3,
则即∴-1≤m≤1.
∴实数m的取值范围是[-1,1].
12.(2017·天津卷,16)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放
时长(分钟)
广告播放时
长(分钟)
收视人次(万)
甲
70
5
60
乙
60
5
25
11
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.
(1)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?
[解析] (1)由已知x,y满足的数学关系式为
即
该二元一次不等式组所表示的平面区域为图①中的阴影部分中的整数点.
(2)设总收视人次为z万,则目标函数为z=60x+25y.
考虑z=60x+25y,将它变形为y=-x+,这是斜率为-,随z变化的一族平行直线.为直线在y轴上的截距,
当取得最大值时,z的值就最大.
又因为x,y满足约束条件,所以由图②可知,当直线z=60x+25y经过可行域上的点M时,截距最大,即z最大.
解方程组
得
则点M的坐标为(6,3).
所以,电视台每周播出甲连续剧6次、乙连续剧3次时,才能使总收视人次最多.
11