- 2021-02-26 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
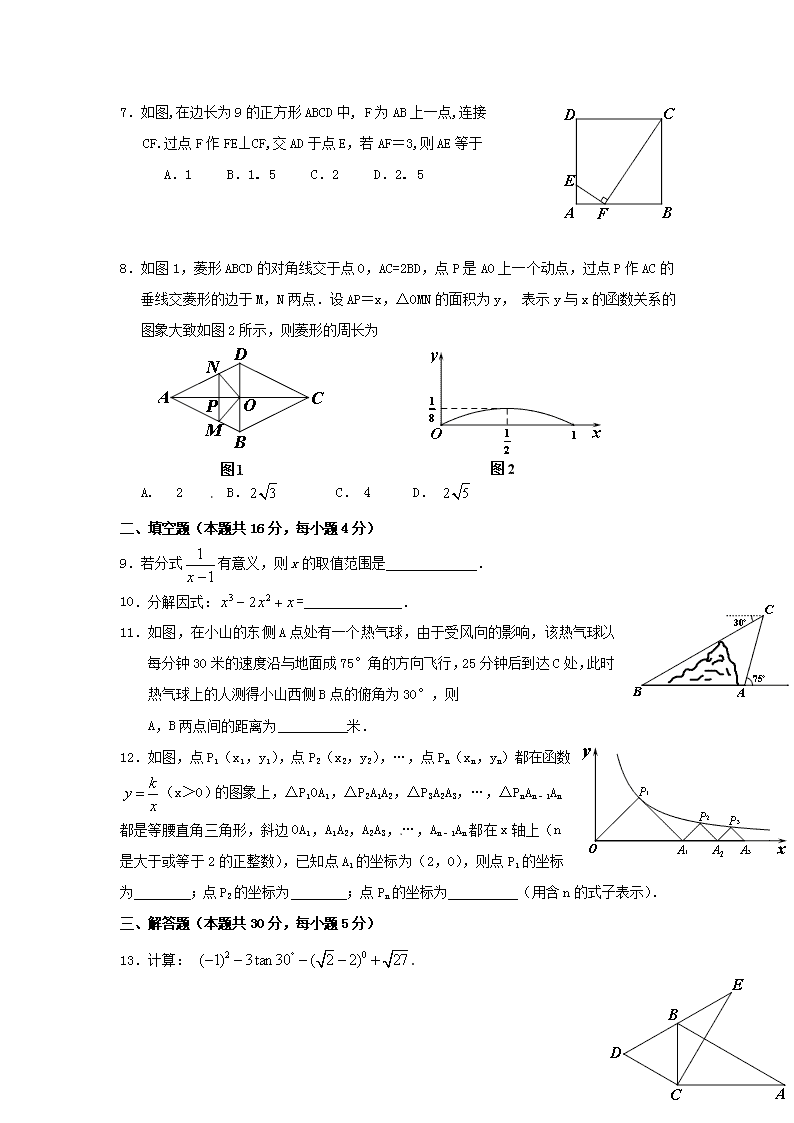
北京房山区2014年中考数学一模试题目
2014年房山区初三毕业会考(一模)试卷 数 学 一、选择题(本题共32分,每小题4分)下列各题均有四个选项,其中只有一个是符合题意的.用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑. 1.的绝对值是 A. B. C. D. 2.转基因作物是利用基因工程将原有作物基因加入其它生物的遗传物质,并将不良基因移除,从而造成品质更好的作物.我国现有转基因作物种植面积约为4 200 000公顷,将4 200 000用科学记数法表示为 A. B. C. D. 3.某班共有学生31名,其中男生11名.老师随机请一名同学回答问题,则男生被选中的概率是 A. B. C. D. 4.如图,直线m∥n,将含有45°角的三角板ABC的 直角顶点C放在直线n上,则∠1+∠2等于 A.30° B. 40° C.45° D.60° 5.将二次函数化为的形式,下列结果正确的是 A. B. C. D. 6.国家统计局公布了2014年1月的居民消费价格指数(CPI),16个省市CPI同比涨幅超过全国平均水平,其中7个省市的涨幅如下表: 地区 北京 广东 上海 浙江 福建 云南 湖北 同比涨幅(﹪) 3.3 3.3 3.0 2.8 2.8 2.8 2.3 则这组数据的众数和中位数分别是 A. 2.8,2.8 B.2.8,2.9 C.3.3,2.8 D.2.8,3.0 7.如图,在边长为9的正方形ABCD中, F为AB上一点,连接 CF.过点F作FE⊥CF,交AD于点E,若AF=3,则AE等于 A.1 B.1. 5 C.2 D.2. 5 图1 图2 8.如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为 A. 2 B. C. 4 D. 二、填空题(本题共16分,每小题4分) 9.若分式有意义,则x的取值范围是 . 10.分解因式:= . 11.如图,在小山的东侧A点处有一个热气球,由于受风向的影响,该热气球以每分钟30米的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则 A,B两点间的距离为 米. 12.如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)都在函数(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示). 三、解答题(本题共30分,每小题5分) 13.计算: . 14.已知:如图,在△DBC中,BC=DC,过点C作CE⊥DC交DB的延长线于点E,过点C作且AC=EC,连结AB. 求证:AB=ED. 15.求不等式组的解集,并求它的整数解. 16. 已知,求代数式的值. 17.如图,点A在反比例函数的图象上. (1) 求反比例函数的解析式; (2)在y轴上是否存在点P,使得△AOP是直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由. 18.列方程或方程组解应用题: 为保证“燕房线”轻轨建设,我区对一条长2 500米的道路进行改造.在改造了1 000米后,为了减少施工对交通造成的影响,采用了新的施工工艺,使每天的工作效率是原来的1.5倍,结果提前5天完成任务.求原来每天改造道路多少米? 四、解答题(本题共20分,每小题5分) 19.已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC, BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F, DF=6. (1) 求AE的长; (2) 求 的值. 20.某校开展“我运动、我健康、我阳光、我快乐”的寒假体育锻炼活动,要求学生每天体育锻炼一小时.开学后小明对本年级学生是否参加体育锻炼的情况进行了调查,并对参加锻炼的学生进行了身体健康测试,绘制成如下统计图. 学生是否参加体育锻炼情况统计图 参加体育锻炼的学生身体健康测试情况统计图 根据以上信息,解答下列问题: (1)小明本次共调查了多少名学生? (2)参加体育锻炼的学生中,有多少人身体健康指数提升? (3)若该校有1 000名学生,请你估计有多少人假期参加体育锻炼?要使两年后参加体育锻炼的人数增加到968人,假设平均每年的增长率相同,求这个增长率. 21.如图, AE是⊙O直径,D是⊙O上一点,连结AD并延长使AD=DC,连结CE交⊙O于点B,连结AB.过点E的直线与AC的延长线交于点F,且∠F=∠CED. (1)求证:EF是⊙O切线; (2)若CD=CF=2,求BE的长. 22. 阅读下列材料: 小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为、、 ,求△ABC的面积. 小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积. 他把这种解决问题的方法称为构图法. 请回答: (1)图1中△ABC的面积为 ; 参考小明解决问题的方法,完成下列问题: (2)图2是一个6×6的正方形网格(每个小正方形的边长为1) . ①利用构图法在答题卡的图2中画出三边长分别为、、的格点△DEF; ②计算△DEF的面积为 . (3)如图3,已知△PQR,以PQ,PR为边向外作正方形PQAF,PRDE,连接EF.若 ,则六边形AQRDEF的面积为__________. 图3 图2 图1 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 如图,抛物线经过、两点,与轴的另一交点是. (1)求抛物线的解析式; (2)若点在第一象限的抛物线上,求点关于直线的对称点的坐标; (3)在(2)的条件下,过点D作于点E,反比例函数的图象经过点E,点在此反比例函数图象上,求的值. 24. 将等腰Rt△ABC和等腰Rt△ADE按图1方式放置,∠A=90°, AD边与AB边重合, AB=2AD=4.将△ADE绕点A逆时针方向旋转一个角度α(0°≤α≤180°),BD的延长线交直线CE于点P. (1)如图2,BD与CE的数量关系是 , 位置关系是 ; (2)在旋转的过程中,当AD⊥BD时,求出CP的长; (3)在此旋转过程中,求点P运动的路线长. 备用图 图2 图1 25. 我们规定:形如 的函数叫做“奇特函数”.当时,“奇特函数”就是反比例函数. (1) 若矩形的两边长分别是2和3,当这两边长分别增加x和y后,得到的新矩形的面积为8 ,求y与x之间的函数关系式,并判断这个函数是否为“奇特函数”; (2) 如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A,C的坐标分别为(9,0)、(0,3). 点D是OA的中点,连结OB,CD交于点E,“奇特函数”的图象经过B,E两点. ① 求这个“奇特函数”的解析式; ② 把反比例函数的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为16,请直接写出点P的坐标. 查看更多