- 2024-04-15 发布 |
- 37.5 KB |
- 4页
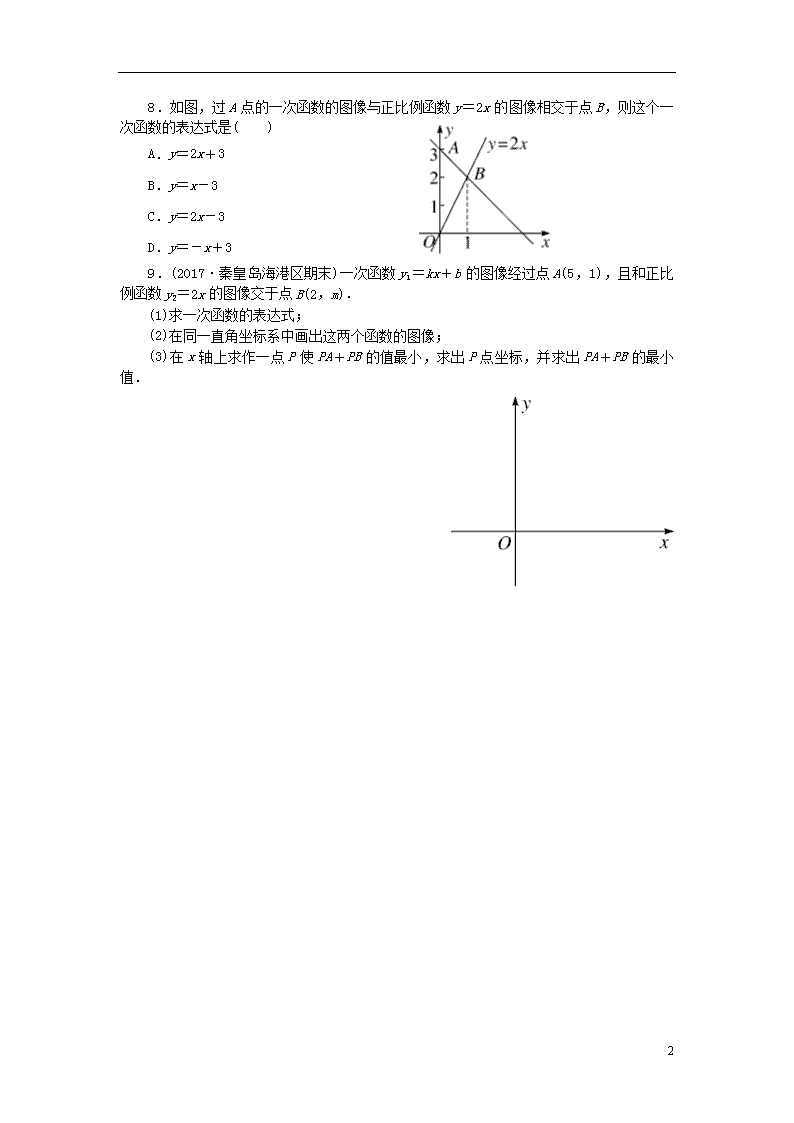

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年八年级数学下册6微专题确定一次函数表达式的方法习题(新版)冀教版
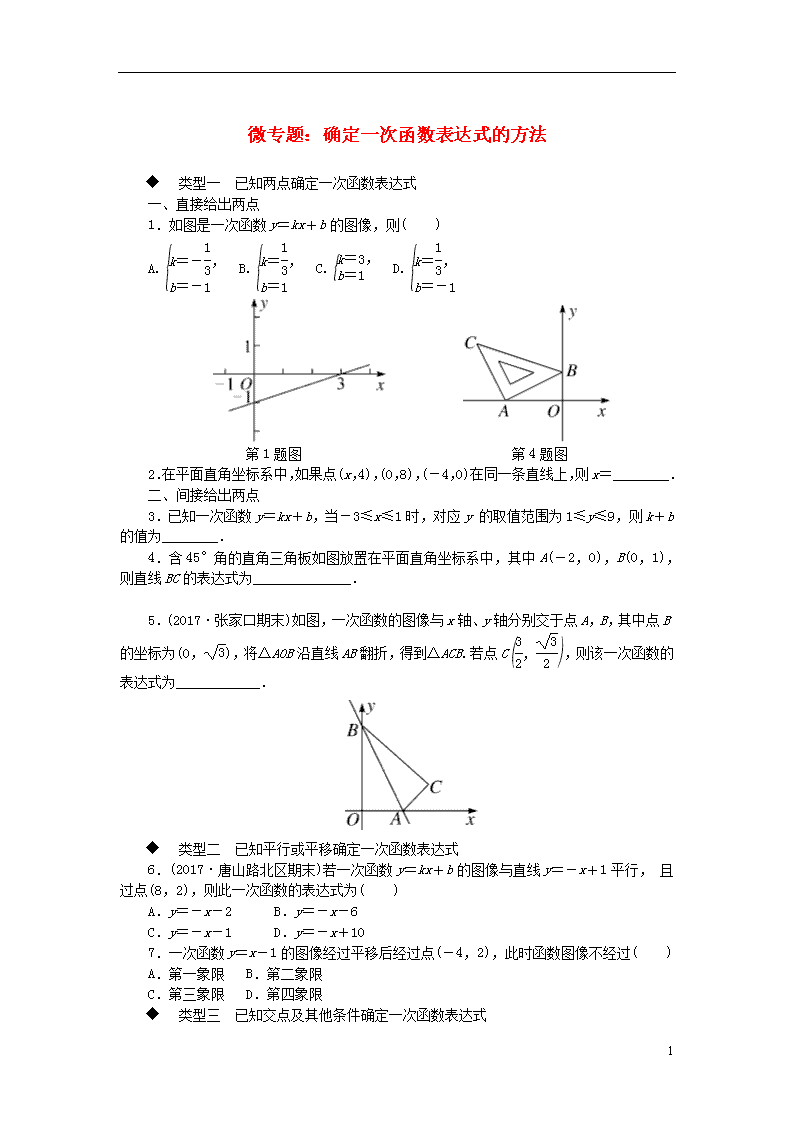
微专题:确定一次函数表达式的方法 类型一 已知两点确定一次函数表达式 一、直接给出两点 1.如图是一次函数y=kx+b的图像,则( ) A. B. C. D. 第1题图 第4题图 2.在平面直角坐标系中,如果点(x,4),(0,8),(-4,0)在同一条直线上,则x=________. 二、间接给出两点 3.已知一次函数y=kx+b,当-3≤x≤1时,对应y 的取值范围为1≤y≤9,则k+b的值为________. 4.含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的表达式为______________. 5.(2017·张家口期末)如图,一次函数的图像与x轴、y轴分别交于点A,B,其中点B的坐标为(0,),将△AOB沿直线AB翻折,得到△ACB.若点C,则该一次函数的表达式为____________. 类型二 已知平行或平移确定一次函数表达式 6.(2017·唐山路北区期末)若一次函数y=kx+b的图像与直线y=-x+1平行, 且过点(8,2),则此一次函数的表达式为( ) A.y=-x-2 B.y=-x-6 C.y=-x-1 D.y=-x+10 7.一次函数y=x-1的图像经过平移后经过点(-4,2),此时函数图像不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 类型三 已知交点及其他条件确定一次函数表达式 4 8.如图,过A点的一次函数的图像与正比例函数y=2x的图像相交于点B,则这个一次函数的表达式是( ) A.y=2x+3 B.y=x-3 C.y=2x-3 D.y=-x+3 9.(2017·秦皇岛海港区期末)一次函数y1=kx+b的图像经过点A(5,1),且和正比例函数y2=2x的图像交于点B(2,m). (1)求一次函数的表达式; (2)在同一直角坐标系中画出这两个函数的图像; (3)在x轴上求作一点P使PA+PB的值最小,求出P点坐标,并求出PA+PB的最小值. 4 参考答案与解析 1.D 2.-2 3. 9或1 解析:①当x=-3时,y=1;当x=1时,y=9,则解得所以k+b=9;②当x=-3时,y=9;当x=1时,y=1,则解得所以k+b=1.故答案为9或1. 4.y=x+1 解析:如图,过C作CD⊥x轴于点D.∵∠CAB=90°,∴∠DAC+∠BAO=∠BAO+∠ABO=90°,∴∠DAC=∠ABO.在△AOB和△CDA中,∴△AOB≌△CDA(AAS),∴AD=BO=1,CD=AO=2,∴C(-3,2).设直线BC表达式为y=kx+b,∴解得∴直线BC表达式为y=-x+1. 5.y=-x+ 解析:过点C作CD⊥x轴于点D.设点A的坐标为(a,0),则OA=a.∵将△AOB沿直线AB翻折得△ACB,C,∴AC=OA=a,CD=,OD=,∴AD=OD-OA=-a.在Rt△ACD中,根据勾股定理得AD2+CD2=AC2,即+=a2,解得a=1,∴点A的坐标为(1,0).设一次函数的表达式为y=kx+b,将A(1,0),B(0,)代入y=kx+b得解得∴该一次函数的表达式为y=-x+. 6.D 7.D 8.D 9.解:(1)∵点B(2,m)在直线y2=2x上,∴m=2×2=4,∴点B的坐标为(2,4).由直线y1=kx+b过点A(5,1),B(2,4),得解得∴一次函数的表达式为y1=-x+6. (2)如图所示. (3)如图,作点A关于x轴的对称点A′,连接BA′交x轴于点P 4 ,此点即为所求.∵A(5,1),∴A′(5,-1).易求得直线BA′的表达式为y=-x+.令y=0,得-x+=0,解得x=,∴P.此时PA+PB=BA′==. 4查看更多