2017-2018学年山西省长治市第二中学高二下学期期末考试数学（文）试题（Word版）

2017-2018学年山西省长治市第二中学高二下学期期末考试数学（文）试题（Word版）

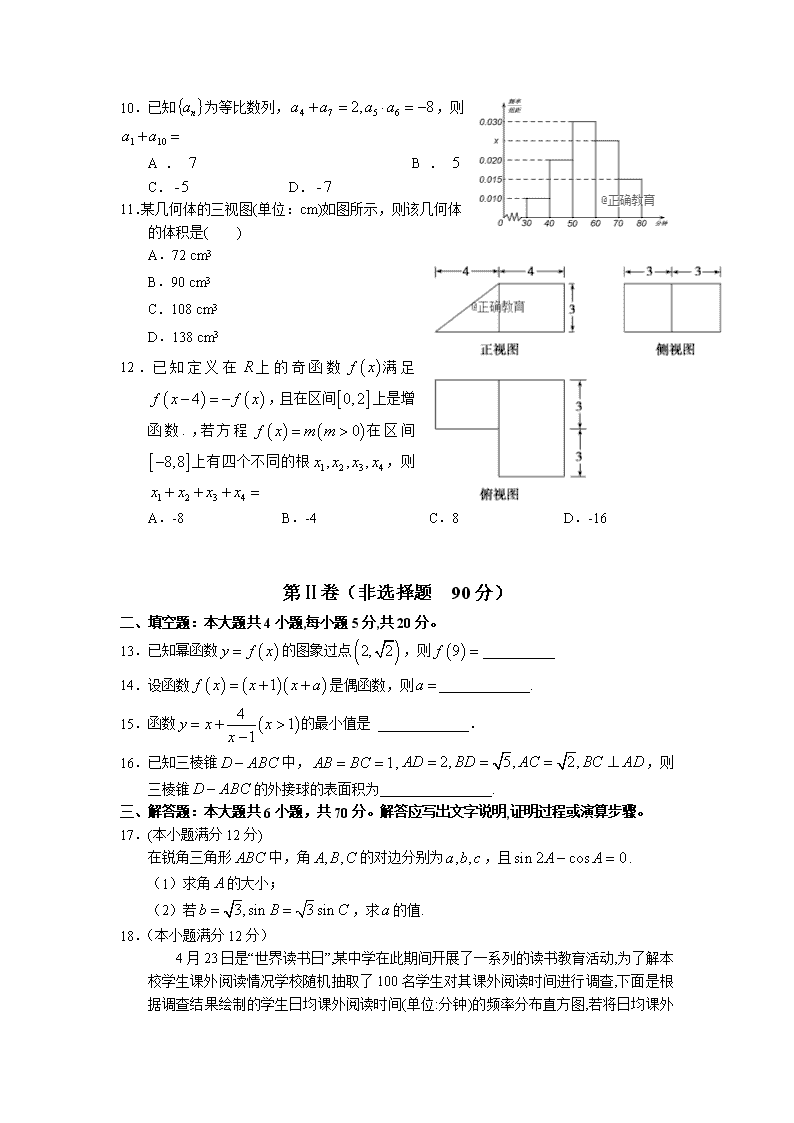
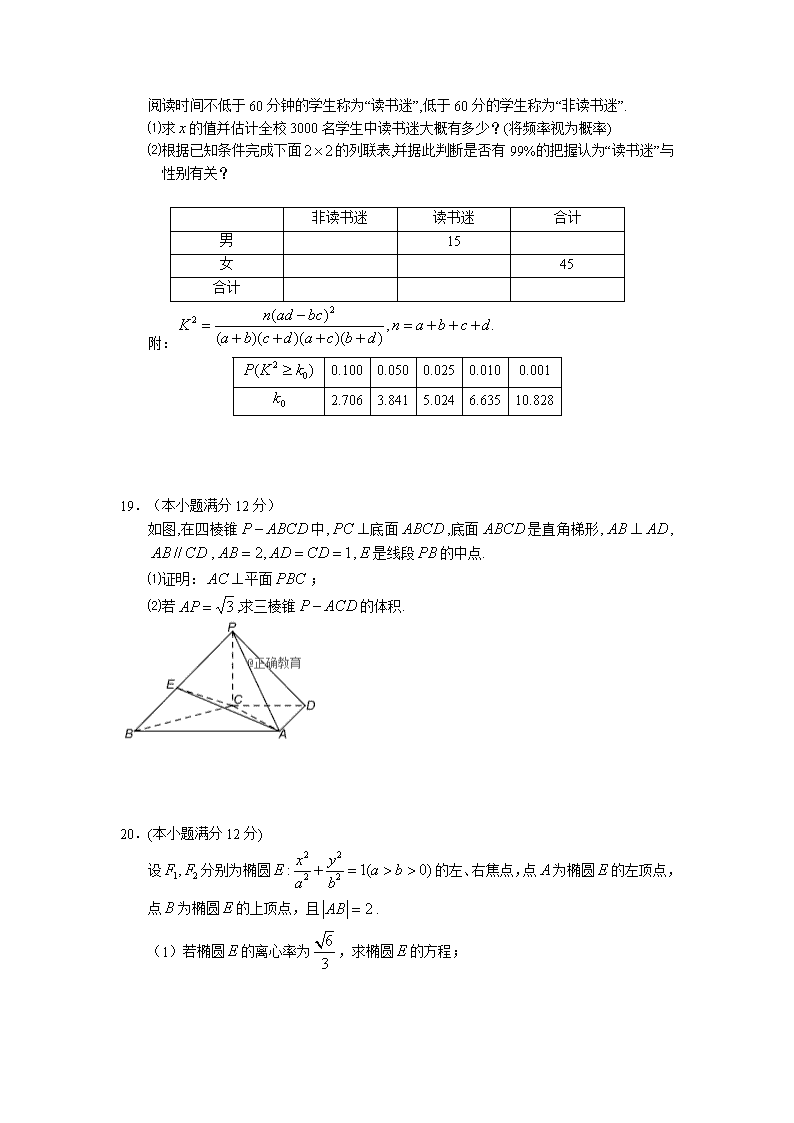
‎2017-2018学年山西省长治市第二中学高二下学期期末考试文科数学试题 命题人：王凤霞 审题人：王宏伟 ‎【考试时间120分钟 满分150分】‎ 第Ⅰ卷（选择题 60分）‎ 一、选择题：本大题共12小题，每小题5分,共60分。在每小题给出的四个选项中，选出符合题目要求的一项。‎ ‎1．已知集合，，则 A． B． C． D．‎ ‎2．已知(为虚数单位) ，则 A． B． C． D． ‎ ‎3．函数是定义在上的奇函数，当时，，则 ‎ A． B． C． D． ‎ ‎4．下列命题中，真命题是 A．若，且，则中至少有一个大于1 ‎ B． ‎ C． 的充要条件是 ‎ D．‎ ‎5．已知抛物线方程为，则该抛物线的焦点坐标为 A． B． C． D． ‎ ‎6．因为对数函数是增函数，而是对数函数，所以是增函数，上面的推理错误的是 A．大前提 B．小前提 C．推理形式 D．以上都是 ‎ ‎7．设，，，则 A． B． C． D． ‎ ‎8．已知向量，，若∥，则 A． B． C． D．‎ ‎9．若则的值为 ．‎ A． B． C． D． ‎ ‎10．已知为等比数列，，则 A． B． C． D．‎ ‎11．某几何体的三视图(单位：cm)如图所示，则该几何体的体积是(　　)‎ A．72 cm3‎ B．90 cm3‎ C．108 cm3‎ D．138 cm3 ‎ ‎12．已知定义在上的奇函数满足，且在区间上是增函数.，若方程在区间上有四个不同的根，则 A．-8 B．-4 C．8 D．-16‎ 第Ⅱ卷（非选择题 90分）‎ 二、填空题：本大题共4小题,每小题5分,共20分。‎ ‎13．已知幂函数的图象过点，则 ‎ ‎14．设函数是偶函数，则_____________.‎ ‎15．函数的最小值是 _____________．‎ ‎16．已知三棱锥中，,，则三棱锥的外接球的表面积为________________.‎ 三、解答题：本大题共6小题，共70分。解答应写出文字说明,证明过程或演算步骤。‎ ‎17．(本小题满分12分)‎ 在锐角三角形中，角的对边分别为，且.‎ ‎（1）求角的大小；‎ ‎（2）若，求的值.‎ ‎18．（本小题满分12分）‎ ‎4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分的学生称为“非读书迷”.‎ ‎⑴求的值并估计全校3000名学生中读书迷大概有多少？(将频率视为概率)‎ ‎⑵根据已知条件完成下面的列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关？‎ 非读书迷 读书迷 合计 男 ‎15‎ 女 ‎45‎ 合计 附：‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.001‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ ‎19．（本小题满分12分）‎ 如图,在四棱锥中,底面,底面是直角梯形,,,,是线段的中点.‎ ‎⑴证明：平面；‎ ‎⑵若,求三棱锥的体积.‎ ‎20．(本小题满分12分) ‎ 设分别为椭圆的左、右焦点，点为椭圆的左顶点，点为椭圆的上顶点，且.‎ ‎（1）若椭圆的离心率为，求椭圆的方程；‎ ‎（2）设为椭圆上一点，且在第一象限内，直线与轴相交于点，若以为直径的圆经过点，证明：点在直线上.‎ ‎21．(本小题满分12分)‎ 设函数在点处的切线方程为.‎ ‎（1）求的值，并求的单调区间；‎ ‎（2）证明：当时，.‎ 请考生从第22、23题中任选一题做答，如果多做，则按所做的第一题计分.‎ ‎22．（本小题满分10分）选修4-4：坐标系与参数方程 已知直线的参数方程是 ，在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎（1）将曲线的极坐标方程化为直角坐标方程；‎ ‎（2）设直线与轴的交点是，是曲线上一动点，求的最大值.‎ ‎23．（本小题满分10分）选修4-5： 不等式选讲 设函数.‎ ‎（1）解不等式；‎ ‎（2）求函数的最大值.‎ ‎2017—2018学年第二学期高二期末考试文科数学试题答案 一、1—5 CBDAC 6—10 ACDCD 11—12 BA 二、13. 14. 15. 16. ‎ 三、17.⑴ , ‎ 又因为为锐角三角形， ， ， ；----------6分 ‎⑵， ， ， 。--------12分 ‎18. ⑴ ， -------------3分 ‎ ， ；--------------------6分 ‎⑵‎ 非读书迷 读书迷 合计 男 ‎40‎ ‎15‎ ‎55‎ 女 ‎20‎ ‎25‎ ‎45‎ 合计 ‎60‎ ‎40‎ ‎100‎ ‎--------------------------------------------------------------------------------------------------------9分 ‎ ， 有99%的把握认为“读书迷”与性别有关。---------------------------------------------------------------------------------------12分 ‎19. ⑴证明：取的中点，连接，,四边形为正方形，,‎ ‎;---------------------------------------(6分)‎ ‎⑵,,在中，,而,.-------(12分)‎ ‎20.（1）点为椭圆的左顶点，点为椭圆的上顶点，，又 ， ， 椭圆 的方程为： .-------------- ---------------------------------------4分 ‎（2）证明：由题意知，从而椭圆的方程为：，则：‎ ‎，，‎ 设，由题意知，则直线的斜率，直线的斜率， 直线的方程为：，当时， ，‎ 即点，直线的斜率 ，以为直径的圆经过点，‎ ‎ ---------------------------------------8分 化简得： ，①‎ 又为椭圆上一点，且在第一象限内， ，②‎ 由①②解得，，即点在直线上.‎ ‎--------------------------12分 ‎ 21.⑴，由已知，，故，‎ ‎，当时，，当时，，故在单调递减，在单调递减；------------（6分）‎ ‎⑵，即，设，‎ ‎，所以在递增，在递减，当。-------------------------------（12分）‎ ‎22.⑴；-------------------------------------5分 ‎⑵由题意知，‎ ‎，‎ 当时，。--------------------------------10分 ‎23.⑴①当，；‎ ‎②当，；‎ ‎③当时，，；‎ 综上，不等式的解集为；-----------------------------5分 ‎⑵，由其图知，。---------------10分