数学理卷·2018届湖南省长沙市一中高二上学期期末考试（2017-01）word版

数学理卷·2018届湖南省长沙市一中高二上学期期末考试（2017-01）word版

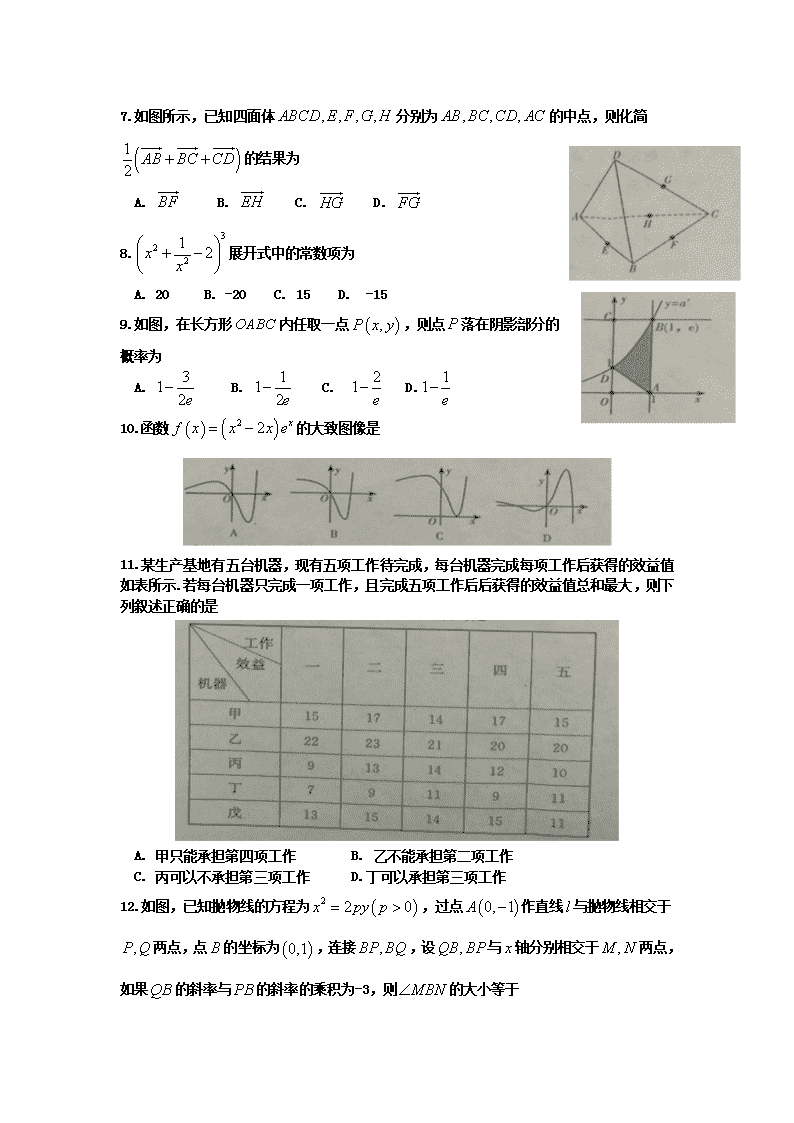
长沙市第一中学 2016——2017 学年度高二第一学期期末考试 理科数学 第Ⅰ卷（选择题 共 60 分） 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分.在每个小题给出的四个选项中，有 且只有一项符合题目要求. 1.命题 的否定形式是 A. B. C. D. 2.若复数 （其中 是实数），则复数 在复平面内所对应的点位于 A. 第一象限 B. 第二象限 C.第三象限 D.第四象限 3.设实数 实数 实数 满足 ，则 是 的 A.充分不必要条件 B. 必要不充分条件 C. 充要条件 D.既不充分也不必要条件 4.已知曲线 在点 处的切线与直线 垂直，则 的值是 A. B. C. D. 5.我们把平面内与直线的方向向量垂直的非零向量称为直线的法向量.在平面直角坐标系 中，利用求动点轨迹方程的方法，可以求出过点 ，且法向量为 的直线 （点法式）方程为： ，化简得 .类比以上方法， 在空间直角坐标系中，经过点 ，且法向量为 的平面的方程为 A. B. C. D. 6.将数字 排成三行两列，要求每行的数字互不相同，每列的数字也互不相同， 则不同的排列方法共有 A. 12 种 B. 18 种 C. 24 种 D. 36 种 ( ) ( )" , "n N f n N f n n∗ ∗∀ ∈ ∉ ≤且 ( ) ( ),n N f n N f n n∗ ∗∀ ∈ ∉ >且 ( ) ( ),n N f n N f n n∗ ∗∀ ∈ ∉ >或 ( ) ( )0 0 0 0,n N f n N f n n∗ ∗∃ ∈ ∉ >且 ( ) ( )0 0 0 0,n N f n N f n n∗ ∗∃ ∈ ∉ >或 2a i ib i + = −− ,a b a bi+ :p 1, 1, :x y q> > ,x y 2x y+ > p q 3y x= ( ),a b 3 1 0x y+ + = a 1− 1± 1 3± ( )3,4A − ( )1, 2n = − ( ) ( )( )1 3 2 4 0x y× + + − − = 2 11 0x y− + = ( )1,2,3A ( )1, 2,1n = − − 2 2 0x y z+ − − = 2 2 0x y z− − − = 2 2 0x y z+ + − = 2 2 0x y z+ + + = 1,1,2,2,3,3 7.如图所示，已知四面体 分别为 的中点，则化简 的结果为 A. B. C. D. 8. 展开式中的常数项为 A. 20 B. -20 C. 15 D. -15 9.如图，在长方形 内任取一点 ，则点 落在阴影部分的 概率为 A. B. C. D. 10.函数 的大致图像是 11.某生产基地有五台机器，现有五项工作待完成，每台机器完成每项工作后获得的效益值 如表所示.若每台机器只完成一项工作，且完成五项工作后后获得的效益值总和最大，则下 列叙述正确的是 A. 甲只能承担第四项工作 B. 乙不能承担第二项工作 C. 丙可以不承担第三项工作 D.丁可以承担第三项工作 12.如图，已知抛物线的方程为 ，过点 作直线 与抛物线相交于 两点，点 的坐标为 ，连接 ，设 与 轴分别相交于 两点， 如果 的斜率与 的斜率的乘积为-3，则 的大小等于 , , , ,ABCD E F G H , , ,AB BC CD AC ( )1 2 AB BC CD+ +   BF EH HG FG 3 2 2 1 2x x  + −   OABC ( ),P x y P 31 2e − 11 2e − 21 e − 11 e − ( ) ( )2 2 xf x x x e= − ( )2 2 0x py p= > ( )0, 1A − l ,P Q B ( )0,1 ,BP BQ ,QB BP x ,M N QB PB MBN∠ A. B. C. D. 第Ⅱ卷（非选择题 共 90 分） 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分. 13.为了研究某种细菌在特定环境下随时间变化的繁殖情况，得到如下实验数据： 由该五组数据解得 关于 的线性回归方程为 ，则实验数据中 的值 为 . 14.若双曲线 的右支上一点 到直线 的距离为 ，则 的值 为 . 15.在直角坐标系 中，曲线 上的点均在圆 外，且对 上任意一 点 ， 到直线 的距离等于该点与圆 上点的距离的最小值，则曲线 的方程 为 . 16.某商场从生产厂家以每件 20 元购进一批商品，若该商品的零售价为 元，销量 （单 位：件）与零售价 （单位：元）有如下关系： ，则该商品零售价 定为 元时利润最大. 三、解答题：本大题共 6 小题，共 70 分.解答应写出必要的文字说明或推理、验算过程. 17.（本题满分 10 分）设函数 ，其中 ，若有 都有成立. （1）求正整数 的最大值 ； （2）证明不等式 （其中 ）. 18.（本题满分 12 分）设 ，在 上 恒成立， 函数 在其定义域上存在极值. （1）若 为真命题，求实数 的取值范围； 6 π 4 π 3 π 5 12 π y t ˆ 0.85 0.25y t= − m 2 2 1x y− = ( ),P a b y x= 2 a b+ xoy 1C ( )2 2 2 : 5 9C x y− + = 1C M M 2x = − 2C 1C p Q p 28300 170Q p p= − = ( ) 1 1 1 1 2 3 1f n n n n = + + ++ + + n N ∗∈ ( ) 24 af n > a 0a ( ) 0 24 af n > n N ∗∈ ( ): 1p f x ax= + ( ]0,2 ( ) 0f x ≥ q ( ) 2lnag x ax xx = − + p a （2）如果“ ”为真命题，“ ”为假命题，求实数 的取值范围. 19.（本题满分 12 分） 根据某电子商务平台的调查统计显示，参与调查的 1000 位上网购物者的年龄情况如下 图： （1）已知 三个年龄段的上网购物者人数成等差数列，求 的值； （2）该电子商务平台将年龄在 之间的人 群定义为高消费人群，其他年龄段定义为潜在消费人 群，为了鼓励潜在消费人群的消费，该平台决定发放 代金券，高消费人群每人发放 50 元代金券，潜在消 费人群每人发放 80 元代金券.已经采用分层抽样的方 法从参与调查的 1000 位上网购物者中抽取了 10 人，现 在要在这 10 人中随机抽取 3 人进行回访，求此三人获 得代金券总和 的分布列. 20.（本题满分 12 分）如图，在斜三棱柱 中，侧面 与侧面 都是菱形， （1）求证： （2）若 ，求二面角 的余 弦值. 21.（本题满分 12 分） 已知椭圆 的离心率为 ，椭圆 和抛物线 交于 两点，且直线 恰好通过椭圆 的右焦点 . （1）求椭圆 的标准方程； （2）已知椭圆 的左焦点为 ，左、右顶点分别为 ，经过点 的直线 与椭圆 p q∨ p q∧ a [ ) [ ) [ )30,40 , 40,50 , 50,60 ,a b [ )30,50 X 1 1 1ABC A B C− 1 1ACC A 1 1BCC B 1 1 1 60 , 2.ACC CC B AC∠ = ∠ = = 1 6AB = 1 1C AB A− − ( )2 2 2 2: 1 0x yE a ba b + = > > 1 2 E 2 9 4y x= ,M N MN E 2F E E 1F ,A B 1F l E 交于 两点，记 与 的面积分别为 ，求 的最大值. 22.（本题满分 12 分）已知函数 为自然对数的底数. （1）讨论 的单调性； （2）若函数 的图象与直线 交于 两点，线段 中点的横坐标为 ，证明： （ 为函数 的导函数）. ,C D ABD∆ ABC∆ 1 2,S S 1 2S S− ( ) ( ) ( )2 ,a xf x xe a R e−= ∈ ( )g x ( ) ( ) 2lnf x g x ax= − ( )y m m R= ∈ ,A B AB 0x ( )0 0f x′ < ( )0f x′ ( )f x