- 2023-12-17 发布 |
- 37.5 KB |
- 17页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
辽宁省大连二十高2017届高三上学期月考物理试卷(12月份)
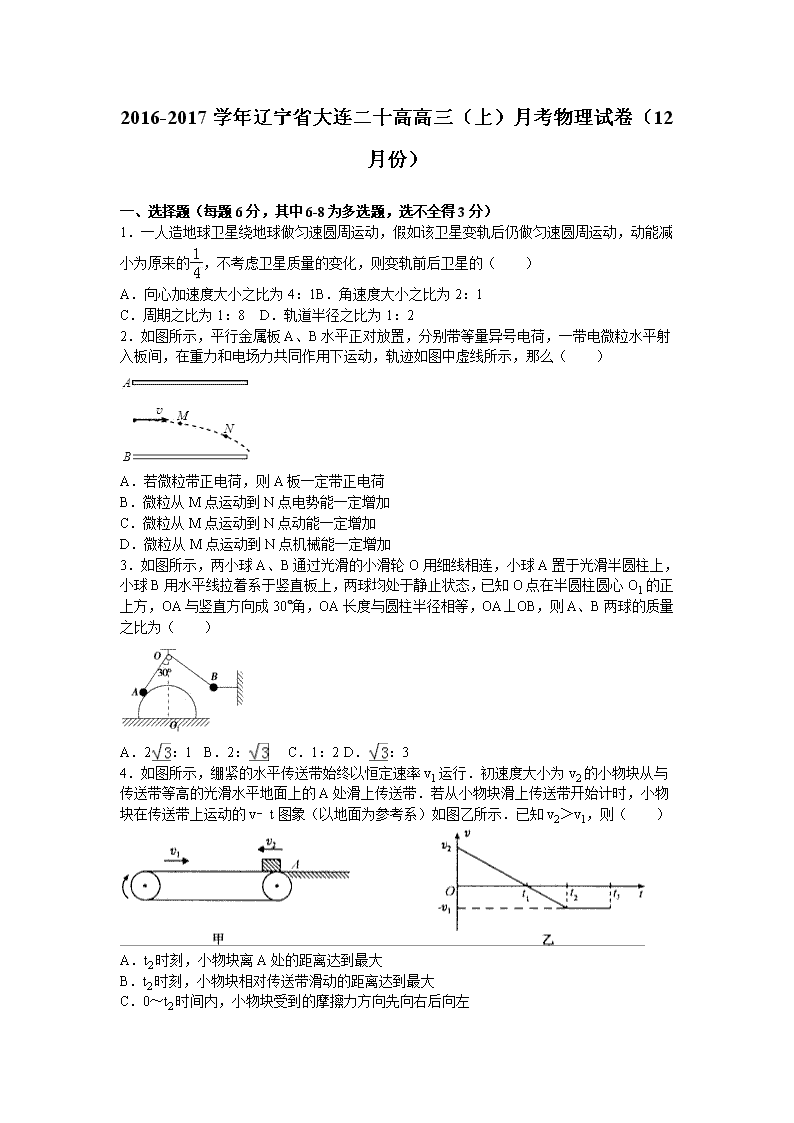
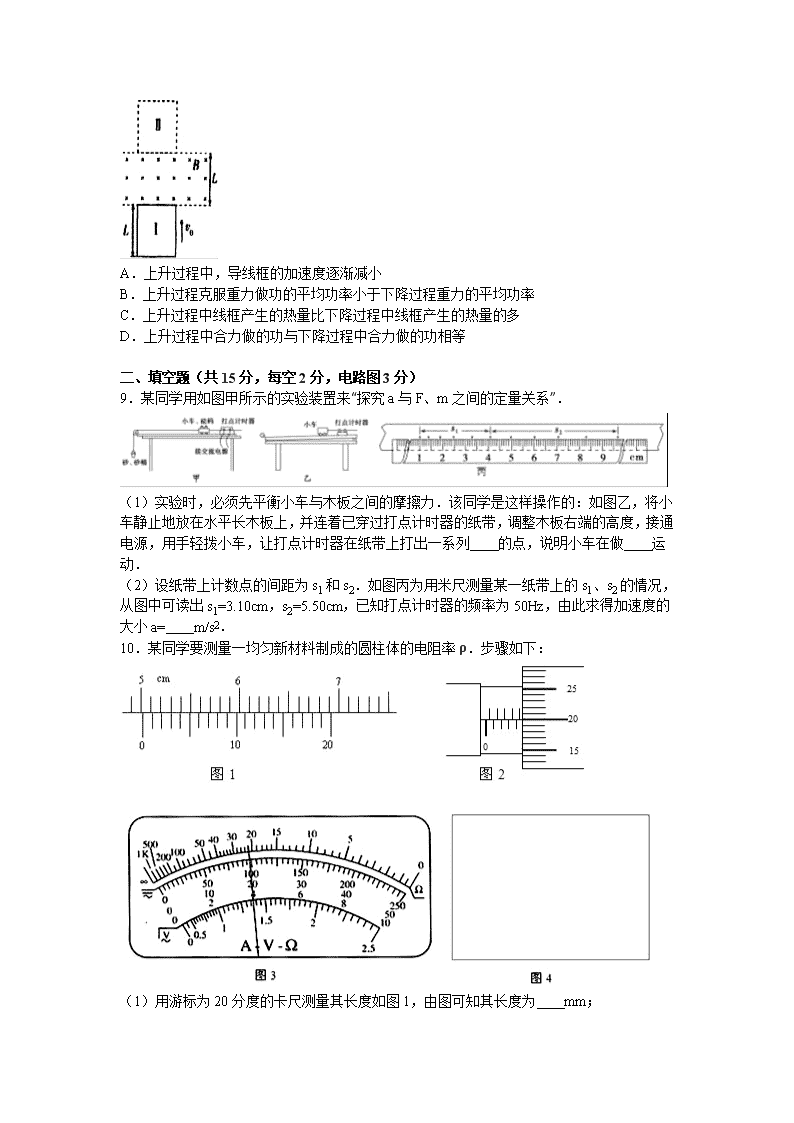
2016-2017学年辽宁省大连二十高高三(上)月考物理试卷(12月份) 一、选择题(每题6分,其中6-8为多选题,选不全得3分) 1.一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后仍做匀速圆周运动,动能减小为原来的,不考虑卫星质量的变化,则变轨前后卫星的( ) A.向心加速度大小之比为4:1 B.角速度大小之比为2:1 C.周期之比为1:8 D.轨道半径之比为1:2 2.如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( ) A.若微粒带正电荷,则A板一定带正电荷 B.微粒从M点运动到N点电势能一定增加 C.微粒从M点运动到N点动能一定增加 D.微粒从M点运动到N点机械能一定增加 3.如图所示,两小球A、B通过光滑的小滑轮O用细线相连,小球A置于光滑半圆柱上,小球B用水平线拉着系于竖直板上,两球均处于静止状态,已知O点在半圆柱圆心O1的正上方,OA与竖直方向成30°角,OA长度与圆柱半径相等,OA⊥OB,则A、B两球的质量之比为( ) A.2:1 B.2: C.1:2 D.:3 4.如图所示,绷紧的水平传送带始终以恒定速率v1运行.初速度大小为v2的小物块从与传送带等高的光滑水平地面上的A处滑上传送带.若从小物块滑上传送带开始计时,小物块在传送带上运动的v﹣t图象(以地面为参考系)如图乙所示.已知v2>v1,则( ) A.t2时刻,小物块离A处的距离达到最大 B.t2时刻,小物块相对传送带滑动的距离达到最大 C.0~t2时间内,小物块受到的摩擦力方向先向右后向左 D.0~t3时间内,小物块始终受到大小不变的摩擦力作用 5.如图所示,质量、初速度大小都相同的A、B、C三个小球,在同一水平面上,A球竖直上抛,B球以倾斜角θ斜向上抛,空气阻力不计,C球沿倾角为θ的光滑固定斜面上滑,它们上升的最大高度分别为hA、hB、hC,则( ) A.hA=hB=hC B.hA=hB<hC C.hA=hB>hC D.hA=hC>hB 6.1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖.若一束粒子由左端射入质谱仪后的运动轨迹如图所示,则下列说法中正确的是( ) A.该束带电粒子带负电 B.速度选择器的P1极板带正电 C.在B2磁场中运动半径越大的粒子,质量越大 D.在B2磁场中运动半径越大的粒子,荷质比越小 7.如图所示,电源电动势E=3V,小灯泡L标有“2V、0.4W”,开关S接l,当变阻器调到R=4Ω时,小灯泡L正常发光;现将开关S接2,小灯泡L和电动机M均正常工作.则( ) A.电源内阻为1Ω B.电动机的内阻为4Ω C.电动机正常工作电压为1V D.电源效率约为93.3% 8.如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平面(纸面)垂直,磁场边界的间距为L.一个质量为m、边长也为L的正方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直,且线框上、下边始终与磁场的边界平行.t=0时刻导线框的上边恰好与磁场的下边界重合(图中位置I),导线框的速度为v0.经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置Ⅱ),导线框的速度刚好为零.此后,导线框下落,经过一段时间回到初始位置I(不计空气阻力),则( ) A.上升过程中,导线框的加速度逐渐减小 B.上升过程克服重力做功的平均功率小于下降过程重力的平均功率 C.上升过程中线框产生的热量比下降过程中线框产生的热量的多 D.上升过程中合力做的功与下降过程中合力做的功相等 二、填空题(共15分,每空2分,电路图3分) 9.某同学用如图甲所示的实验装置来“探究a与F、m之间的定量关系”. (1)实验时,必须先平衡小车与木板之间的摩擦力.该同学是这样操作的:如图乙,将小车静止地放在水平长木板上,并连着已穿过打点计时器的纸带,调整木板右端的高度,接通电源,用手轻拨小车,让打点计时器在纸带上打出一系列 的点,说明小车在做 运动. (2)设纸带上计数点的间距为s1和s2.如图丙为用米尺测量某一纸带上的s1、s2的情况,从图中可读出s1=3.10cm,s2=5.50cm,已知打点计时器的频率为50Hz,由此求得加速度的大小a= m/s2. 10.某同学要测量一均匀新材料制成的圆柱体的电阻率ρ.步骤如下: (1)用游标为20分度的卡尺测量其长度如图1,由图可知其长度为 mm; (2)用螺旋测微器测量其直径如图2,由图可知其直径为 mm; (3)用多用电表的电阻“×10”挡,按正确的操作步骤测此圆柱体的电阻,表盘的示数如图3,则该电阻的阻值约为 Ω. (4)该同学想用伏安法更精确地测量其电阻R,现有的器材及其代号和规格如下: 待测圆柱体电阻R 直流电源E(电动势4V,内阻不计) 电流表A1(量程0~4mA,内阻约50Ω) 电流表A2(量程0~10mA,内阻约30Ω) 电压表V1(量程0~3V,内阻约10kΩ) 电压表V2(量程0~15V,内阻约25kΩ) 滑动变阻器R1(阻值范围0~15Ω,允许通过的最大电流2.0A) 滑动变阻器R2(阻值范围0~2kΩ,允许通过的最大电流0.5A) 开关S 导线若干 为使实验误差较小,要求测得多组数据进行分析,请在图4中画出测量的电路图,并标明所用器材的代号. 三、计算题(23题12分,24题15分,25题20分) 11.如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上.物体A被水平速度为v0的子弹射中并嵌在其中.已知物体A的质量是物体B的质量的,子弹的质量是物体B的质量的,求: (1)A物体获得的最大速度; (2)弹簧压缩到最短时B的速度. 12.如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB平齐,静止放于倾角为53°的光滑斜面上.一长为L=9cm的轻质细绳一端固定在O点,另一端系一质量为m=1kg的小球,将细绳拉至水平,使小球在位置C由静止释放,小球到达最低点D时,细绳刚好被拉断.之后小球在运动过程中恰好沿斜面方向将弹簧压缩,最大压缩量为x=5cm.(g=10m/s2,sin 53°=0.8,cos 53°=0.6)求: (1)细绳受到的拉力的最大值; (2)D点到水平线AB的高度h; (3)弹簧所获得的最大弹性势能Ep. 13.如图所示,质量M=0.2kg的长木板静止于水平地面上,与地面间的动摩擦因数μ1=0.1.一质量m=0.1kg、带电荷量q=+2×10﹣3C的滑块(可看作质点)在t=0时刻以v0=5m/s的初速度滑上长木板的同时加上一个水平向右的匀强电场,滑块与长木板间的动摩擦因数μ2=0.4,所加电场的电场强度E=100N/C,取g=10m/s2,设最大静摩擦力等于滑动摩擦力,最终滑块没有从长木板上滑下,求; (1)长木板的最小长度; (2)滑块从滑上长木板到静止经历的时间; (3)整个过程中产生的热量. 2016-2017学年辽宁省大连二十高高三(上)月考物理试卷(12月份) 参考答案与试题解析 一、选择题(每题6分,其中6-8为多选题,选不全得3分) 1.一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后仍做匀速圆周运动,动能减小为原来的,不考虑卫星质量的变化,则变轨前后卫星的( ) A.向心加速度大小之比为4:1 B.角速度大小之比为2:1 C.周期之比为1:8 D.轨道半径之比为1:2 【考点】人造卫星的加速度、周期和轨道的关系;万有引力定律及其应用. 【分析】根据万有引力提供向心力,通过线速度的变化得出轨道半径的变化,从而得出向心加速度、周期、角速度的变化. 【解答】解:根据得,v=,动能减小为原来的,则线速度减为原来的,则轨道半径变为原来的4倍.则轨道半径之比为1:4. 根据解得,,T=,则向心加速度变为原来的,角速度变为原来的,周期变为原来的8倍.故C正确,A、B、D错误. 故选C. 2.如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( ) A.若微粒带正电荷,则A板一定带正电荷 B.微粒从M点运动到N点电势能一定增加 C.微粒从M点运动到N点动能一定增加 D.微粒从M点运动到N点机械能一定增加 【考点】带电粒子在混合场中的运动;功能关系;机械能守恒定律. 【分析】微粒在平行金属板间受到重力与电场力的作用,根据微粒运动轨迹与微粒受到的重力与电场力间的关系分析答题. 【解答】解:微粒在极板间受到竖直向下的重力作用与电场力作用,由图示微粒运动轨迹可知,微粒向下运动,说明微粒受到的合力竖直向下,重力与电场力的合力竖直向下; A、如果微粒带正电,A板带正电荷,微粒受到的合力向下,微粒运动轨迹向下,A板带负电,但如果电场力小于重力,微粒受到的合力向下,微粒运动轨迹向下,则A板既可以带正电,也可能带负电,故A错误; B、如果微粒受到的电场力向下,微粒从M点运动到N点过程中电场力做正功,微粒电势能减小,如果微粒受到的电场力向上,则电势能增加,故B错误; C、微粒受到的合力向下,微粒从M点运动到N点过程中合外力做正功,微粒的动能增加,故C正确; D、微粒从M点运动到N点过程动能增加,重力势能减小,机械能不一定增加,故D错误. 故选:C. 3.如图所示,两小球A、B通过光滑的小滑轮O用细线相连,小球A置于光滑半圆柱上,小球B用水平线拉着系于竖直板上,两球均处于静止状态,已知O点在半圆柱圆心O1的正上方,OA与竖直方向成30°角,OA长度与圆柱半径相等,OA⊥OB,则A、B两球的质量之比为( ) A.2:1 B.2: C.1:2 D.:3 【考点】共点力平衡的条件及其应用;力的合成与分解的运用. 【分析】根据绳子上的拉力的特点可知绳子对A的拉力与对B的拉力大小相等,然后分别对A和B进行受力分析,结合共点力的平衡即可求出两个小球的质量关系. 【解答】解:对A分析,如图所示,由几何关系可知拉力T和支持力N与水平方向的夹角相等,夹角为60°, 则N和T相等,有:2Tsin60°=mAg, 解得T=, 再隔离对B分析,根据共点力平衡有:Tcos60°=mBg, 则, 可知: =, 故选:A 4.如图所示,绷紧的水平传送带始终以恒定速率v1运行.初速度大小为v2的小物块从与传送带等高的光滑水平地面上的A处滑上传送带.若从小物块滑上传送带开始计时,小物块在传送带上运动的v﹣t图象(以地面为参考系)如图乙所示.已知v2>v1,则( ) A.t2时刻,小物块离A处的距离达到最大 B.t2时刻,小物块相对传送带滑动的距离达到最大 C.0~t2时间内,小物块受到的摩擦力方向先向右后向左 D.0~t3时间内,小物块始终受到大小不变的摩擦力作用 【考点】牛顿第二定律;匀变速直线运动的图像. 【分析】0~t1时间内木块向左匀减速直线运动,受到向右的摩擦力,然后向右匀加速,当速度增加到与皮带相等时,一起向右匀速,摩擦力消失. 【解答】解:A、t1时刻小物块向左运动到速度为零,离A处的距离达到最大,故A错误; B、t2时刻前小物块相对传送带向左运动,之后相对静止,故B正确; C、0~t2时间内,小物块受到的摩擦力方向始终向右,故C错误; D、t2~t3时间内小物块不受摩擦力作用,故D错误; 故选:B. 5.如图所示,质量、初速度大小都相同的A、B、C三个小球,在同一水平面上,A球竖直上抛,B球以倾斜角θ斜向上抛,空气阻力不计,C球沿倾角为θ的光滑固定斜面上滑,它们上升的最大高度分别为hA、hB、hC,则( ) A.hA=hB=hC B.hA=hB<hC C.hA=hB>hC D.hA=hC>hB 【考点】机械能守恒定律. 【分析】三个球的机械能均守恒,根据球到达最高点时的速度关系和机械能守恒定律分析对比,即可得出结论. 【解答】解:对于A球,该球竖直上抛运动,根据机械能守恒定律可得: mghA=mv02; B球做斜抛运动,水平方向做匀速直线运动,到达最高点时的速度为v0cosθ 根据机械能守恒定律得: =mghB+ 对于C球:机械能守恒定律可得: mghC=mv02; 则有:hA=hC>hB; 故选:D. 6.1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖.若一束粒子由左端射入质谱仪后的运动轨迹如图所示,则下列说法中正确的是( ) A.该束带电粒子带负电 B.速度选择器的P1极板带正电 C.在B2磁场中运动半径越大的粒子,质量越大 D.在B2磁场中运动半径越大的粒子,荷质比越小 【考点】质谱仪和回旋加速器的工作原理;带电粒子在匀强磁场中的运动. 【分析】A、根据带电粒子在磁场中的偏转方向确定带电粒子的正负. B、根据在速度选择器中电场力和洛伦兹力平衡确定P1极板的带电情况. CD、在磁场中,根据洛伦兹力提供向心力,求出粒子的轨道半径,看与什么因素有关. 【解答】解:A、根据带电粒子在磁场中的偏转方向,磁场的方向垂直纸面向外,根据左手定则知,该粒子带正电.故A错误. B、根据左手定则知,带电粒子在P1P2区域所受的洛伦兹力方向竖直向上,则电场力的方向竖直向下,知电场强度的方向竖直向下,所以速度选择器的P1极板带正电.故B正确. C、根据得,,知r越大,荷质比越小.故C错误,D正确. 故选BD. 7.如图所示,电源电动势E=3V,小灯泡L标有“2V、0.4W”,开关S接l,当变阻器调到R=4Ω时,小灯泡L正常发光;现将开关S接2,小灯泡L和电动机M均正常工作.则( ) A.电源内阻为1Ω B.电动机的内阻为4Ω C.电动机正常工作电压为1V D.电源效率约为93.3% 【考点】电功、电功率;闭合电路的欧姆定律. 【分析】(1)小灯泡L正常发光,其电压为额定电压,功率为额定功率,由公式P=UI可求出电路中的电流.根据闭合电路欧姆定律求解电源的电阻. (2)电动机为非纯电阻电路,注意公式的应用与选取即可 【解答】解:小灯泡的额定电流为I= 电阻为RL= A、当接1时 E=I(RL+R+r) 代入数据解得r=1Ω,故A正确; B、当接2时灯泡正常发光,流过的电流为I=0.2A 电源内阻分的电压为U=Ir=0.2×1V=0.2V 故电动机分的电压为U动=E﹣UL﹣U=3﹣2﹣0.2V=0.8V 故电阻R<,故BC错误; D、电源的效率η= 故选:AD 8.如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平面(纸面)垂直,磁场边界的间距为L.一个质量为m、边长也为L的正方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直,且线框上、下边始终与磁场的边界平行.t=0时刻导线框的上边恰好与磁场的下边界重合(图中位置I),导线框的速度为v0.经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置Ⅱ),导线框的速度刚好为零.此后,导线框下落,经过一段时间回到初始位置I(不计空气阻力),则( ) A.上升过程中,导线框的加速度逐渐减小 B.上升过程克服重力做功的平均功率小于下降过程重力的平均功率 C.上升过程中线框产生的热量比下降过程中线框产生的热量的多 D.上升过程中合力做的功与下降过程中合力做的功相等 【考点】导体切割磁感线时的感应电动势;电磁感应中的能量转化. 【分析】解答本题应分析线框的受力,根据牛顿第二定律得到加速度与速度的关系,即可分析加速度的变化情况; 根据能量守恒分析线框返回原位置时速率关系,由动能定理判断上升和下降两过程合力做功关系. 根据安培力表达式FA=,分析线框克服安培力做功的关系. 【解答】解:A、上升过程中,线框所受的重力和安培力都向下,线框做减速运动.设加速度大小为a,根据牛顿第二定律得:mg+=ma,a=g+,由此可知,线框速度v减小时,加速度a也减小,故A正确. B、下降过程中,线框做加速运动,则有mg﹣=ma′,a′=g﹣,由此可知,下降过程加速度小于上升过程加速度,上升过程位移与下降过程位移相等,则上升时间短,下降时间长,上升过程与下降过程重力做功相同,则上升过程克服重力做功的平均功率大于下降过程重力的平均功率,故B错误; C、线框产生的焦耳热等于克服安培力做功,对应与同一位置,上升过程安培力大于下降过程安培力,上升与下降过程位移相等,则上升过程克服安培力做功大于下降过程克服安培力做功,上升过程中线框产生的热量比下降过程中线框产生的热量的多,故C正确; D、在电磁感应现象中,线框中产生电能,根据能量守恒定律可知,线框返回原位置时速率减小,则上升过程动能的变化量大小大于下降过程动能的变化量大小,根据动能定理得知,上升过程中合力做功较大,故D错误. 故选:AC. 二、填空题(共15分,每空2分,电路图3分) 9.某同学用如图甲所示的实验装置来“探究a与F、m之间的定量关系”. (1)实验时,必须先平衡小车与木板之间的摩擦力.该同学是这样操作的:如图乙,将小车静止地放在水平长木板上,并连着已穿过打点计时器的纸带,调整木板右端的高度,接通电源,用手轻拨小车,让打点计时器在纸带上打出一系列 点迹均匀 的点,说明小车在做 匀速 运动. (2)设纸带上计数点的间距为s1和s2.如图丙为用米尺测量某一纸带上的s1、s2的情况,从图中可读出s1=3.10cm,s2=5.50cm,已知打点计时器的频率为50Hz,由此求得加速度的大小a= 2.40 m/s2. 【考点】探究加速度与物体质量、物体受力的关系. 【分析】(1)平衡摩擦力时,调整木板右端的高度,接通电源,用手轻拨小车,当小车带动纸带匀速下滑时说明平衡摩擦力; (2)根据匀变速直线运动的特点,利用逐差法可以求出其加速度的大小. 【解答】解:(1)平衡摩擦力时,应将绳从小车上拿去,不要挂钩码,将长木板的右端垫高至合适位置,使小车重力沿斜面分力和摩擦力抵消,若小车做匀速直线运动,此时打点计时器在纸带上打出一系列点迹均匀的点, (2)根据图象可知,S2=5.50cm,打点计时器的频率为50Hz,每5个点取一个计数点,则T=0.1s,加速度的大小a= 故答案为:(1)点迹均匀 匀速 (2)2.40 10.某同学要测量一均匀新材料制成的圆柱体的电阻率ρ.步骤如下: (1)用游标为20分度的卡尺测量其长度如图1,由图可知其长度为 50.15 mm; (2)用螺旋测微器测量其直径如图2,由图可知其直径为 4.700 mm; (3)用多用电表的电阻“×10”挡,按正确的操作步骤测此圆柱体的电阻,表盘的示数如图3,则该电阻的阻值约为 220 Ω. (4)该同学想用伏安法更精确地测量其电阻R,现有的器材及其代号和规格如下: 待测圆柱体电阻R 直流电源E(电动势4V,内阻不计) 电流表A1(量程0~4mA,内阻约50Ω) 电流表A2(量程0~10mA,内阻约30Ω) 电压表V1(量程0~3V,内阻约10kΩ) 电压表V2(量程0~15V,内阻约25kΩ) 滑动变阻器R1(阻值范围0~15Ω,允许通过的最大电流2.0A) 滑动变阻器R2(阻值范围0~2kΩ,允许通过的最大电流0.5A) 开关S 导线若干 为使实验误差较小,要求测得多组数据进行分析,请在图4中画出测量的电路图,并标明所用器材的代号. 【考点】测定金属的电阻率. 【分析】(1)游标卡尺读数的方法是主尺读数加上游标读数,不需估读; (2)螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数; (3)欧姆表读数时要注意乘以倍率; (4)根据提供的电源选择电压表;根据电路中的电流选择电流表;根据实验器材确定滑动变阻器接法,根据待测电阻阻值与电表内阻关系确定电流表接法,作出电路图. 【解答】解:(1)20分度的游标卡尺最小分度是0.05mm,主尺读数是5.0cm=50mm;游标读数是0.05×3=0.15mm;总读数是:50mm+0.15mm=50.15mm (2)由图示螺旋测微器可知,螺旋测微器固定刻度示数为4.5mm,可动刻度示数为20.0×0.01mm=0.200mm,螺旋测微器示数为4.5mm+0.200m=4.700mm; (3)欧姆表读数:22×10=220Ω (4)电源的电动势是4V,所以要选择量程是3V的电压表V1; 电路中的电流约为:.所以要选择量程是10mA的电流表A2. 题目要求测得多组数据进行分析,所以需要采用分压式接法,滑动变阻器选择电阻值比较小的R 1. 由于,所以采用电流表外接法.电路图如图: 故答案为:(1)50.15;(2)4.700;(3)220;(4)如图 三、计算题(23题12分,24题15分,25题20分) 11.如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上.物体A被水平速度为v0的子弹射中并嵌在其中.已知物体A的质量是物体B的质量的,子弹的质量是物体B的质量的,求: (1)A物体获得的最大速度; (2)弹簧压缩到最短时B的速度. 【考点】动量守恒定律;功的计算. 【分析】(1)子弹刚射入物块A时,A具有最大速度v,此过程中子弹与A的动量守恒,根据动量守恒定律即可求解最大速度; (2)以子弹、滑块A、B和弹簧组成的系统为研究对象,当三者速度相等时,弹簧被压缩到最短,则弹性势能最大,根据动量守恒可正确解答. 【解答】解:(1)根据题意可知,B的质量为4m,A的质量为3m,子弹的质量为m,子弹刚射入物块A时,A具有最大速度v,此过程中子弹与A的动量守恒,以子弹的初速度方向为正,根据动量守恒定律得: mv0=(m+3m)v 解得:v= (2)对子弹、滑块A、B和弹簧组成的系统,A、B速度相等时弹簧被压缩到最短. 设B的质量为m, 根据动量守恒定律可得: mv0=(m+mA+mB)v 由此解得:v= 答:(1)A物体获得的最大速度为; (2)弹簧压缩到最短时B的速度为. 12.如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB平齐,静止放于倾角为53°的光滑斜面上.一长为L=9cm的轻质细绳一端固定在O点,另一端系一质量为m=1kg的小球,将细绳拉至水平,使小球在位置C由静止释放,小球到达最低点D时,细绳刚好被拉断.之后小球在运动过程中恰好沿斜面方向将弹簧压缩,最大压缩量为x=5cm.(g=10m/s2,sin 53°=0.8,cos 53°=0.6)求: (1)细绳受到的拉力的最大值; (2)D点到水平线AB的高度h; (3)弹簧所获得的最大弹性势能Ep. 【考点】机械能守恒定律;牛顿第二定律. 【分析】(1)根据机械能守恒定律求出小球在D点的速度,再根据竖直方向上的合力提供向心力,运用牛顿第二定律求出绳子的最大拉力. (2)球在运动过程中恰好沿斜面方向将弹簧压缩,知绳子断裂后,做平抛运动,由平抛运动的规律求h. (3)根据速度的合成求出A点的速度,根据系统机械能守恒求出弹簧的最大弹性势能. 【解答】解:(1)小球由C到D,由机械能守恒定律得:mgL=m 解得:v1=…① 在D点,由牛顿第二定律得:F﹣mg=m…② 由①②解得:F=30 N 由牛顿第三定律知细绳所能承受的最大拉力为 30 N. (2)由D到A,小球做平抛运动,则得 vy2=2gh…③ 由 tan53°=…④ 联立解得h=0.16m (3)小球从C点到将弹簧压缩至最短的过程中,小球与弹簧系统的机械能守恒,即: Ep=mg(L+h+xsin 53°) 代入数据得:Ep=2.9 J. 答:(1)细绳受到的拉力的最大值为30 N. (2)D点到水平线AB的高度h为0.16m. (3)弹簧所获得的最大弹性势能Ep为2.9 J 13.如图所示,质量M=0.2kg的长木板静止于水平地面上,与地面间的动摩擦因数μ1=0.1.一质量m=0.1kg、带电荷量q=+2×10﹣3C的滑块(可看作质点)在t=0时刻以v0=5m/s的初速度滑上长木板的同时加上一个水平向右的匀强电场,滑块与长木板间的动摩擦因数μ2=0.4,所加电场的电场强度E=100N/C,取g=10m/s2,设最大静摩擦力等于滑动摩擦力,最终滑块没有从长木板上滑下,求; (1)长木板的最小长度; (2)滑块从滑上长木板到静止经历的时间; (3)整个过程中产生的热量. 【考点】匀强电场中电势差和电场强度的关系;牛顿运动定律的综合应用;功能关系. 【分析】(1)根据牛顿第二定律分别求出滑块和木板的加速度,求出速度相等时经过的时间,根据位移关系求解相对位移即可; (2)根据牛顿第二定律求出二者减速运动的加速度,根据速度时间关系求解二者减速运动的时间,进而求出滑块从滑上长木板到静止经历的时间; (3)根据能量关系可得产生的总热量. 【解答】解:(1)滑块滑动过程中的加速度大小为a1,根据牛顿第二定律可得: μ2mg﹣qE=ma1, 解得:a1=2m/s2, 木板的加速度为a2,则:μ2mg﹣μ1(m+M)g=Ma2, 解得:a2=0.5m/s2, 当二者速度相同时经过的时间为t1,则: v0﹣a1t1=a2t1, 解得:t1=2s; 共同的速度为:v=a2t1=0.5×2m/s=1m/s; 所以木板的长度至少为:L==; (2)以后二者共同运动的加速度为a3,根据牛顿第二定律可得: μ1(m+M)g﹣qE=(m+M)a3, 解得:a3=, 二者减速运动的时间为t2,则: t2=, 所以滑块从滑上长木板到静止经历的时间t=t1+t2=5s; (3)物块减速的位移为:x=, 根据能量关系可得,整个过程中产生的热为Q=+qE() 即:Q==2.75 J. 答:(1)长木板的最小长度为5m; (2)滑块从滑上长木板到静止经历的时间为5s; (3)整个过程中产生的热量为2.75J. 2016年12月31日查看更多