高中数学必修2教案：3_2_2直线的两点式方程

高中数学必修2教案：3_2_2直线的两点式方程

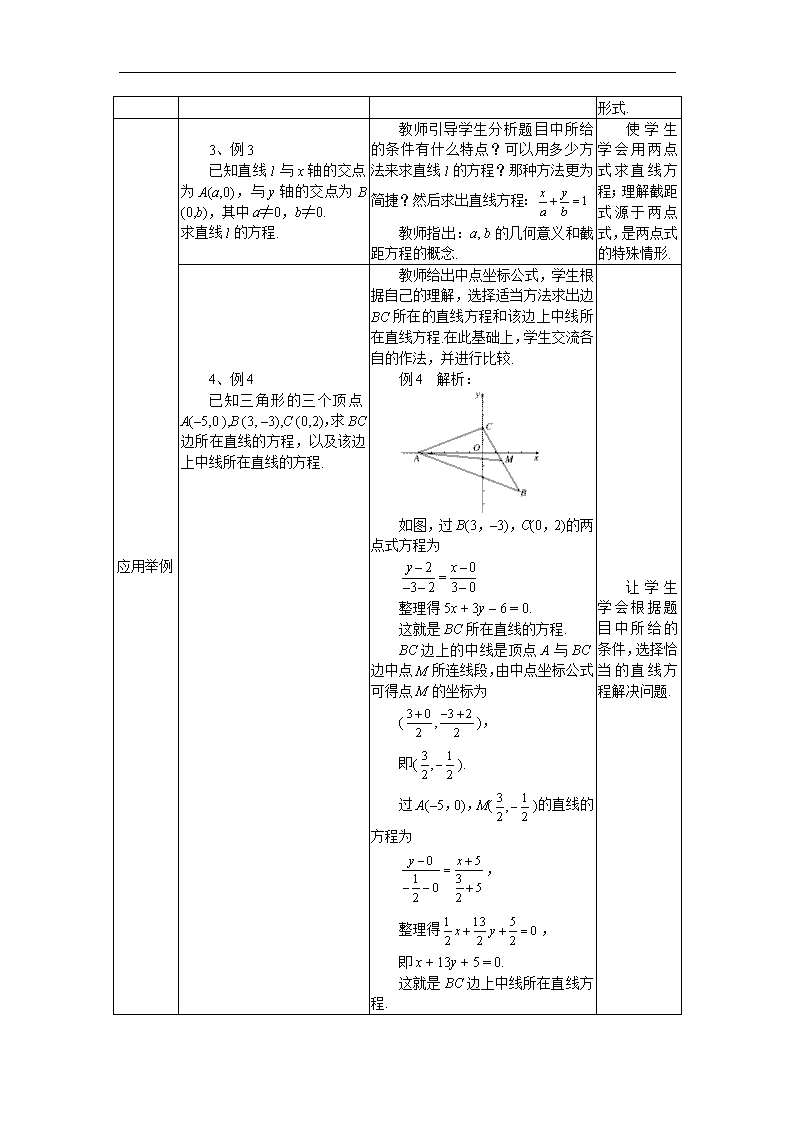
‎3.2.2 直线的两点式方程 ‎(一)教学目标 ‎1．知识与技能 ‎（1）掌握直线方程的两点式的形式特点及适用范围；‎ ‎（2）了解直线方程截距式的形式特点及适用范围。‎ ‎2．过程与方法 让学生在应用旧知识的探究过程中获得新的结论，并通过新旧知识的比较、分析、应用获得新知识的特点.‎ ‎3．情态与价值观 ‎（1）认识事物之间的普通联系与相互转化；‎ ‎（2）培养学生用联系的观点看问题。‎ ‎（二）教学重点、难点：‎ ‎1．重点：直线方程两点式。‎ ‎2．难点：两点式推导过程的理解。‎ ‎（三）教学设想 教学环节 教学内容 师生互动 设计意图 提出问题引入课题得出概念 ‎1．利用点斜式解答如下问题：‎ ‎（1）已知直线l经过两点P1 (1，2)，P2 (3，5)，求直线l的方程.‎ ‎（2）已知两点P1 (x1，x2)，P2 (x1，x2)其中(x1≠x2，y1≠y2). 求通过这两点的直线方程.‎ 教师引导学生：根据已有的知识，要求直线方程，应知道什么条件？能不能把问题转化已经解决的问题？在此基础上，学生根据已知两点的坐标，先判断是否存在斜率，然后求出直线的斜率，从而可求出直线方程：‎ ‎（1）y – 2 =(x–1)‎ ‎（2）y – y1 =‎ 教师指出：当y1≠y2时，方程可写成 由于这个直线方程由两点确定，所以我们把它叫直线的两点式方程，简称两点式（two-point form）.‎ ‎ 遵循由浅及深，由特殊到一般的认知规律。使学生在已有的知识基础上获得新结论，达到温故知新的目的。‎ 概念深入 ‎2．若点P1 (x1，x2)，P2 (x2，y2)中有x1 = x2，或y1 = y2，此时这两点的直线方程是什么？‎ ‎ 教师引导学生通过画图、观察和分析，发现x1 = x2时，直线与x轴垂直，所以直线方程为：x = x1；当y1 = y2时，直线与y轴垂直，直线方程为：y = y1.‎ ‎ ‎ ‎ 使学生懂得两点式的适用范围和当已知的两点不满足两点式的条件时它的方程形式.‎ 应用举例 ‎3、例3 ‎ 已知直线l与x轴的交点为A(a,0)，与y轴的交点为B (0,b)，其中a≠0，b≠0.‎ 求直线l的方程.‎ 教师引导学生分析题目中所给的条件有什么特点？可以用多少方法来求直线l的方程？那种方法更为简捷？然后求出直线方程：‎ 教师指出：a, b的几何意义和截距方程的概念.‎ 使学生学会用两点式求直线方程；理解截距式源于两点式，是两点式的特殊情形.‎ ‎4、例4 ‎ 已知三角形的三个顶点A(–5,0 ),B (3, –3),C (0,2)，求BC边所在直线的方程，以及该边上中线所在直线的方程.‎ 教师给出中点坐标公式，学生根据自己的理解，选择适当方法求出边BC所在的直线方程和该边上中线所在直线方程.在此基础上，学生交流各自的作法，并进行比较.‎ 例4 解析：‎ 如图，过B(3，–3)，C(0，2)的两点式方程为 整理得5x + 3y – 6 = 0.‎ 这就是BC所在直线的方程.‎ BC边上的中线是顶点A与BC边中点M所连线段，由中点坐标公式可得点M的坐标为 ‎()，‎ 即().‎ 过A(–5，0)，M()的直线的方程为 ‎，‎ 整理得，‎ 即x + 13y + 5 = 0.‎ 这就是BC边上中线所在直线方程.‎ 让学生学会根据题目中所给的条件，选择恰当的直线方程解决问题.‎ ‎5、课堂练习 第102页第1、2、3题 学生独立完成，教师检查、反馈.‎ 归纳总结 ‎6、小结 教师提出：（1）到目前为止，我们所学过的直线方程的表达形式有多少种？它们之间有什么关系？‎ ‎（2）要求一条直线的方程，必须知道多少个条件？‎ ‎ 增强学生对直线方种四种形式（点斜式、斜截式、两点式、截距式）互相之间的联系的理解.‎ 课后作业 布置作业 见习案3.2的第二课时.‎ 学生课后完成 ‎ 巩固深化，培养学生的独立解决问题的能力.‎ ‎ 备选例题 ‎ 例1 求经过点A (–3，4)，且在坐标轴上截距互为相反数的直线l的方程.‎ ‎【解析】当直线l在坐标轴上截距都不为零时，设其方程为.‎ 将A(–3，4)代入上式，有， 解得a = –7.‎ ‎∴所求直线方程为x – y + 7 = 0.‎ 当直线l在坐标轴上的截距都为零时，设其方程为y = kx.将A(–3，4)代入方程得4 = –3k，即k = .‎ ‎∴所求直线的方程为x，即4x + 3y = 0.故所求直线l的方程为x – y + 7 = 0或4x + 3y = 0.‎ ‎【评析】此题运用了直线方程的截距式，在用截距时，必须注意适用条件：a、b存在且都不为零，否则容易漏解.‎ 例2 如图，某地汽车客运公司规定旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李票费y（元）与行李重量x (kg)的关系用直线AB的方程表示，试求：‎ ‎（1）直线AB的方程；‎ ‎（2）旅客最多可免费携带多少行李？‎ ‎【解析】（1）由图知，A (60，6)，B (80，10)代入两点式可得AB方程为x – 5y – 30 =0‎ ‎（2）由题意令y = 0，得x = 30 即旅客最多可免费携带30kg行李.‎