- 2021-02-26 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学《1_2_2-2 分段函数及映射》课外演练 新人教A版必修1
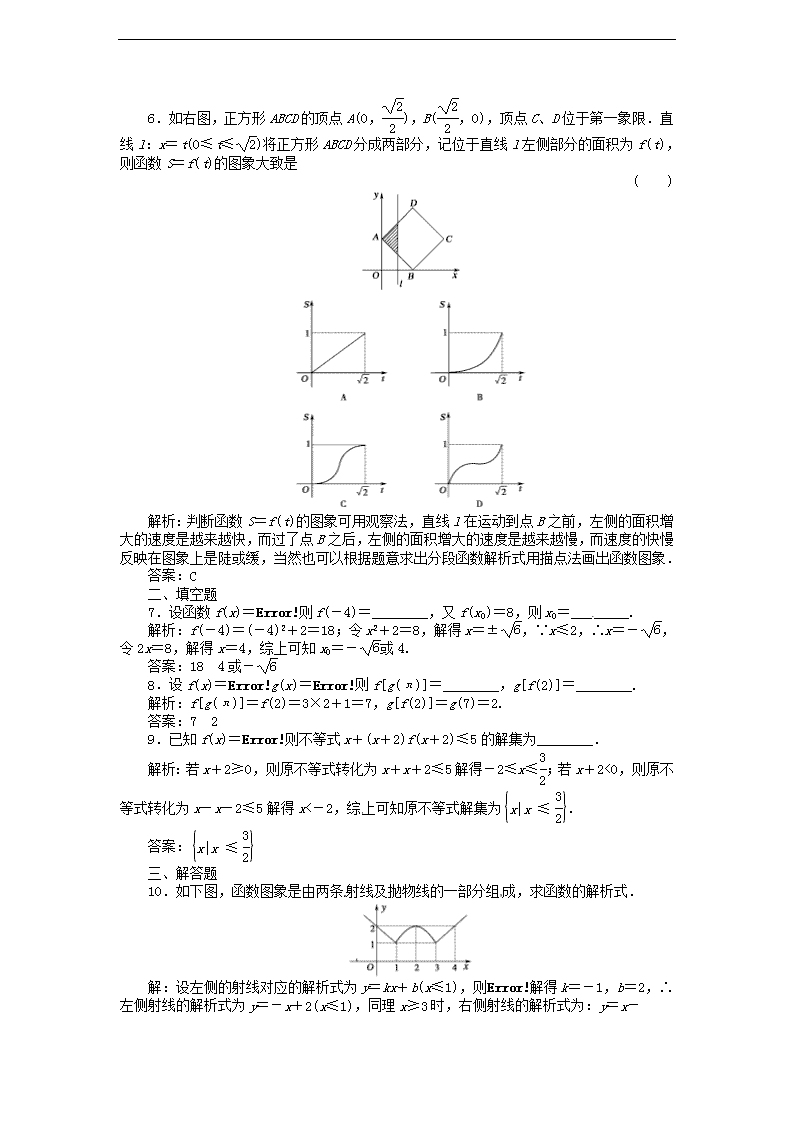
(新课程)高中数学《1.2.2-2 分段函数及映射》课外演练 新人教A版必修1 基础达标 一、选择题 1.已知f(x)=则f[f()]的值是 ( ) A.- B. C. D.- 解析:f()=-1=-;f(-)=-+1=. 答案:C 2.函数f(x)=的值域是 ( ) A.[0,+∞) B.R[来源:学&科&网Z&X&X&K] C.[0,3] D.[0,2]∪{3} 答案:D 3.已知集合A={x|0≤x≤4},B={y|0≤y≤2},按对应关系f不能成为从A至B的映射的一个是 ( ) A.f:x→y=x B.f:x→y=x-2 C.f:x→y= D.f:x→y=|x-2| 解析:取x=0代入y=x-2得y=-2,-2∉B,与映射定义不符. 答案:B 4.如下图,函数y=|x+1|的图象是 ( ) 解析:y=|x+1|= 答案:A 5.若f(x)=φ(x)=则当x<0时,f[φ(x)]为 ( )[来源:Z。xx。k.Com] A.-x B.-x2 C.x D.x2 解析:x<0时,φ(x)=-x2<0,∴f[φ(x)]=-x2. 答案:B 6.如右图,正方形ABCD的顶点A(0,),B(,0),顶点C、D位于第一象限.直线l:x=t(0≤t≤)将正方形ABCD分成两部分,记位于直线l左侧部分的面积为f(t),则函数 S=f(t)的图象大致是 ( ) 解析:判断函数S=f(t)的图象可用观察法,直线l在运动到点B之前,左侧的面积增大的速度是越来越快,而过了点B之后,左侧的面积增大的速度是越来越慢,而速度的快慢反映在图象上是陡或缓,当然也可以根据题意求出分段函数解析式用描点法画出函数图象. 答案:C 二、填空题 7.设函数f(x)=则f(-4)=________,又f(x0)=8,则x0=________. 解析:f(-4)=(-4)2+2=18;令x2+2=8,解得x=±,∵x≤2,∴x=-,令2x=8,解得x=4,综上可知x0=-或4. 答案:18 4或- 8.设f(x)=g(x)=则f[g(π)]=________,g[f(2)]=________. 解析:f[g(π)]=f(2)=3×2+1=7,g[f(2)]=g(7)=2. 答案:7 2 9.已知f(x)=则不等式x+(x+2)f(x+2)≤5的解集为________.[来源:学科网ZXXK] 解析:若x+2≥0,则原不等式转化为x+x+2≤5解得-2≤x≤;若x+2<0,则原不等式转化为x-x-2≤5解得x<-2,综上可知原不等式解集为. 答案: 三、解答题 10.如下图,函数图象是由两条射线及抛物线的一部分组成,求函数的解析式. 解:设左侧的射线对应的解析式为y=kx+b(x≤1),则解得k=-1,b=2,∴左侧射线的解析式为y=-x+2(x≤1),同理x≥3时,右侧射线的解析式为:y=x-2(x≥3).再设抛物线对应的二次函数的解析式为:y=a(x-2)2+2(1≤x≤3,a<0), ∴a+2=1,a=-1,∴抛物线的解析式为y=-x2+4x-2(1≤x≤3). 综上,函数解析式为[来源:学科网] y= 11.已知函数f(x)= 求:(1)f{f[f(-)]}; (2)若f(a)=3,求a的值; (3)求f(x)的定义域及值域. 解:(1)f(-)=-+2=,f()=2×=,f()=2×=1,∴f=1. (2)当a≤-1时,f(a)=a+2≤1,∴f(a)=3无解. 当-1查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档