重庆市巴蜀中学初中部数学教研组整理：八年级数学上（RJ）11

重庆市巴蜀中学初中部数学教研组整理：八年级数学上（RJ）11

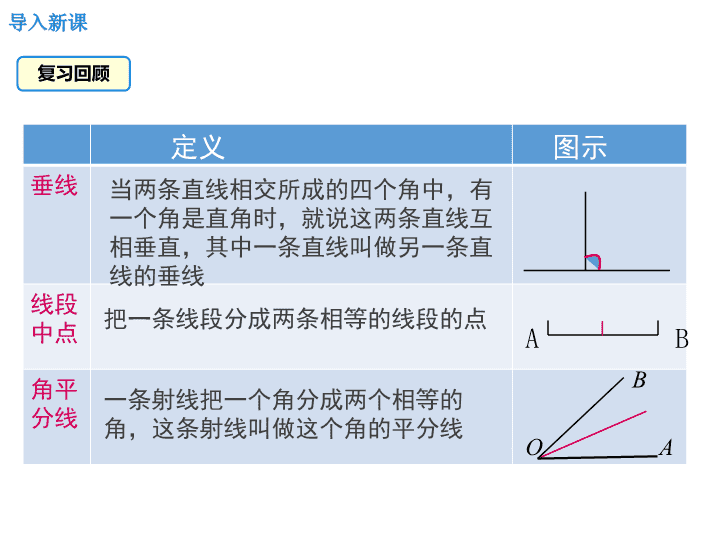
11.1.2 三角形的高、中线与角平分线 第十一章 三角形 导入新课 讲授新课 当堂练习 课堂小结 八年级数学上（RJ） 教学课件 学习目标 1. 掌握三角形的高，中线及角平分线的概念 . （重点） 2. 掌握 三角形的高，中线及角平分线的画法 . 3. 掌握 钝角三角形的两短边上高的画法 . （难点） 复习回顾 导入新课 定义 图示 垂线 线段中点 角平分线 O B A A B 当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线 把一条线段分成两条相等的线段的点 一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线 你还记得 “过一点画已知直线的垂线” 吗 ? 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 0 1 2 3 4 5 放、 靠、 过、 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 0 1 2 3 4 5 画 . 思考： 过三角形的一个顶点，你能画出它的对边的垂线吗 ? 复习导入 导入新课 三角形的高 一 三角形的高的定义 A 从三角形的一个顶点， B C 向它的对边 所在直线作垂线， 顶点 和垂足 D 之间的线段 叫作 三角形的高线 ， 简称三角形的高 . 如右图 , 线段 AD 是 BC 边上的高 . 和垂足的字母 . 注意 ! 标明垂直的记号 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 0 1 2 3 4 5 讲授新课 思考： 你还能画出一条高来吗？ 一个三角形有三个顶点，应该有三条高 . (1) 你能画出这 个三角形的三条高吗 ? (2) 这三条高之间有怎样的位置关系？ O (3) 锐角三角形的三条高是在三角 形的内部还是外部 ? 锐角三角形的三条高交于同一点； 锐角三角形的三条高都在三角形的内部 . 锐角三角形的三条高 如图所示； 直角边 BC 边上的高是 ; 直角边 AB 边上的高是 ; (2) AC 边上的高是 ; 直角三角形的三条高 A B C (1) 画出 直角三角形的三条高 , AB BC 它们有怎样的位置关系？ D 直角三角形的三条高交于直角顶点 . BD 钝角三角形的三条高 (1) 你能画出钝角三角形的三条 高吗？ A B C D E F (2) AC 边上的高呢？ AB 边上呢？ BC 边上呢？ BF CE AD A B C D F (3) 钝角三角形的三条高 交于一点吗？ (4) 它们所在的直线交于 一点吗？ O E 钝角三角形的三条高 不相交于一点； 钝角三角形的三条高所在直线交于一点 . 视频：画 钝角三角形的高 例 1 作 △ ABC 的边 AB 上的高，下列作法中，正确的是 ( 　　 ) 典例精析 方法总结：三角形任意一边上的高必须满足： (1) 过该边所对的顶点； (2) 垂足必须在该边或在该边的延长线上． D 例 2 如图所示，在 △ ABC 中， AB ＝ AC ＝ 5 ， BC ＝ 6 ， AD ⊥ BC 于点 D ，且 AD ＝ 4 ， 若点 P 在边 AC 上移动，则 BP 的最小值为 ____ ． 方法总结：可利用面积相等作桥梁 ( 但不求面积 ) 求三角形的高，此解题方法通常称为“面积法”． 例 3 如图，已知 AD 是 △ ABC 的角平分线， CE 是 △ ABC 的高， ∠ BAC ＝ 60° ， ∠ BCE ＝ 40° ， 求 ∠ ADB 的度数． 解： ∵ AD 是 △ ABC 的角平分线， ∠ BAC ＝ 60° ， ∴∠ DAC ＝ ∠ BAD ＝ 30°. ∵ CE 是 △ ABC 的高， ∠ BCE ＝ 40° ， ∴ ∠ B ＝ 50° ， ∴ ∠ ADB ＝ 180° － ∠ B － ∠ BAD ＝ 180° － 30° － 50° ＝ 100°. 视频：平均分蛋糕 在三角形中，连接一个顶点与它对边中点的线段，叫 作 这个三角形的中线( median ). AE 是 BC 边上的中线. 三角形的“中线” B A C A BE=EC E 三角形的中线 二 (1)在纸上 画出一个锐角三角形，确定它的中线 . 你有什么方法？它有多少条中线？ 它们有怎样的 位置关系 ? 议一议 三条中线， 交于一点 (2) 钝角三角形和直角三角形的中线又是怎样的？ 折一折，画一画，并与同伴交流 . 三角形的三条中线交于一点，这个交点就是三角形的重心 . 要点归纳 典例精析 例 4 在 △ ABC 中， AC ＝ 5cm ， AD 是 △ ABC 的中线，若 △ ABD 的周长比 △ ADC 的周长大 2cm ，则 BA ＝ ________. 提示：将 △ ABD 与 △ ADC 的周长之差转化为边长的差 . 7 c m 三角形的角平分线 三 思考 在一张薄纸上任意画一个三角形，你能设法画出它的一个内角的平分线吗?你能通过折纸的方法得到它吗? B A C 用量角器画最简便，用圆规也能 . 在一张纸上画出一个一个三角形并剪下，将它的一个角对折，使其两边重合 . 折痕 AD 即为三角形的 ∠ A 的平分线 . A B C A D 三角形的角平分线的定义 : 在三角形中，一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段叫 三角形的角平分线 . 1 2 A B C D 注意：“三角形的角平分线”是一条线段 . ∠ 1=∠2 每人准备锐角三角形、钝角三角形和直角三角 形纸片各一个 . (1) 你能分别画出这三个三角形的三条角平分线吗? (2) 你能用折纸的办法得到它们吗 ? (3) 在每个三角形中，这三条角平分线之间有怎样的 位置关系 ? 做一做 三角形的三条角平分线交于同一点 . 三角形角平分线的性质 解： ∵ AD 是 △ ABC 的角平分线， ∠ BAC ＝ 68° ， ∴ ∠ DAC ＝ ∠ BAD ＝ 34°. 在 △ ABD 中， ∠ B +∠ ADB +∠ BAD ＝ 180° ， ∴ ∠ ADB ＝ 180° － ∠ B － ∠ BAD ＝ 180° － 36° － 34° ＝ 110°. 例 5 如图,在△ ABC 中, ∠ BAC = 6 8 °，∠ B = 3 6 °， AD 是△ ABC 的一条角平分线，求 ∠ ADB 的度数 . A B D C 三角形的 重要线段 概念 图形 表示法 三角形 的高线 从三角形的一个顶点向它的对边所在的直线作垂线 , 顶点和垂足 之间的 线段 ∵ AD 是△ ABC 的高线 . ∴AD⊥BC ∠ADB=∠ADC=90°. 三角形 的中线 三角形中 , 连结一个顶点和它对边中的 线段 ∵ AD 是△ ABC 的 BC 上的中线 . ∴ BD=CD= ½ BC. 三角形的 角平分线 三角形一个内角的平分线与它的对边相交 , 这个角顶点与交点之间的 线段 ∵.AD 是△ ABC 的∠ BAC 的平分线 ∴ ∠1=∠2= ½ ∠BAC 知识归纳 当堂练习 1 ．下列说法正确的是 （　　） A ．三角形三条高都在三角形内 B ．三角形三条中线相交于一点 C ．三角形的三条角平分线可能在三角形内，也可 能在三角形外 D ．三角形的角平分线是射线 B 2 ．在△ ABC 中， AD 为中线， BE 为角平分线，则在以下等式中：①∠ BAD =∠ CAD ；②∠ ABE =∠ CBE ；③ BD = DC ；④ AE = EC ．其中正确的是 （　　） A ．①② B ．③④ C ．①④ D ．②③ D 3. 如图，△ ABC 中∠ C =90° ， CD ⊥ AB ，图中线段中可以作为△ ABC 的高的有 （　　） A ． 2 条 B ． 3 条 C ． 4 条 D ． 5 条 4. 下列各组图形中 ， 哪一组图形中 AD 是 △ ABC 的 BC 边上的高 ( ) A D C B A B C D A B C D A B C D A B C D B D 5. 填空 ： （ 1 ）如图①， AD , BE , CF 是△ ABC 的三条中线，则 AB= 2 ＿＿ ,BD= ＿＿ ， AE= ＿＿ (2) 如图②， AD,BE,CF 是△ ABC 的三条角平分线，则∠ 1= ＿＿ ， ∠ 3=_________ ， ∠ ACB=2______. 图① 图② AF DC ∠ 2 2 ∠ 4 AC ∠ ABC 6. 在 Δ ABC 中 ,CD 是中线 , 已知 BC － AC= 5cm , Δ DBC 的周长为 25cm, 求 Δ ADC 的周长 . A D B C 解： ∵ CD 是 △ ABC 的中线， ∴ BD ＝ AD ， ∴△ DBC 的周长＝ BC ＋ BD ＋ CD ＝ 25cm ， 则 BD+CD ＝ 25 － BC . ∴△ ADC 的周长＝ AD ＋ CD ＋ AC ＝ BD ＋ CD ＋ AC ＝ 25 - BC ＋ AC ＝ 25 － ( BC － AC ) ＝ 25 － 5 ＝ 20cm. 7. 如图 , AE 是 △ ABC 的角平分线 . 已知 ∠ B = 45 ° , ∠ C = 60 ° , 求 ∠ BAE 和 ∠ AEB 的度数 . A B C E 解： ∵ Ａ E 是 △ ABC 的角平分线， ∵ ∠ BAC +∠ B +∠ C = 180 ° , ∴ ∠ BAC = 180 ° － ∠ B － ∠ C = 180 ° － 45 ° － 60 ° = 75 ° ， ∴ ∠ BAE = 37.5 ° . ∵ ∠ AEB =∠ CAE +∠ C ， ∠ CAE =∠ BAE = 37.5 °， ∴ ∠ AEB = 37.5 ° + 60 ° = 97.5 ° . ∴ ∠ CAE= ∠ BAE= ∠ BAC. 8. 如图，在△ ABC 中， AD 是△ ABC 的高， AE 是 △ ABC 的角平分线，已知∠ BAC =82° ，∠ C =40° ， 求∠ DAE 的大小 . 解： ∵ AD 是△ ABC 的高， ∴∠ ADC ＝ 90°. ∵ ∠ ADC +∠ C +∠ DAC =180° ， ∴ ∠ DAC =180° － (∠ ADC +∠ C ) =180° － 90° － 40°=50°. ∵ AE 是△ ABC 的角平分线，且∠ BAC =82° ， ∴∠ CAE =41° ， ∴∠ DAE =∠ DAC －∠ CAE =50° － 41°= 9°. B A C D E 课堂小结 三角形重要线段 高 钝角三角形两短边上的高的画法 中线 会把原三角形面积 平分 一边上的中线把原三角形分成两个三角形，这两个三角形的周长差等于原三角形其余两边的差 角平分线