- 2023-08-09 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019九年级数学上册 第六章 反比例函数 3 反比例函数的应用(1)教案 (新版)北师大版
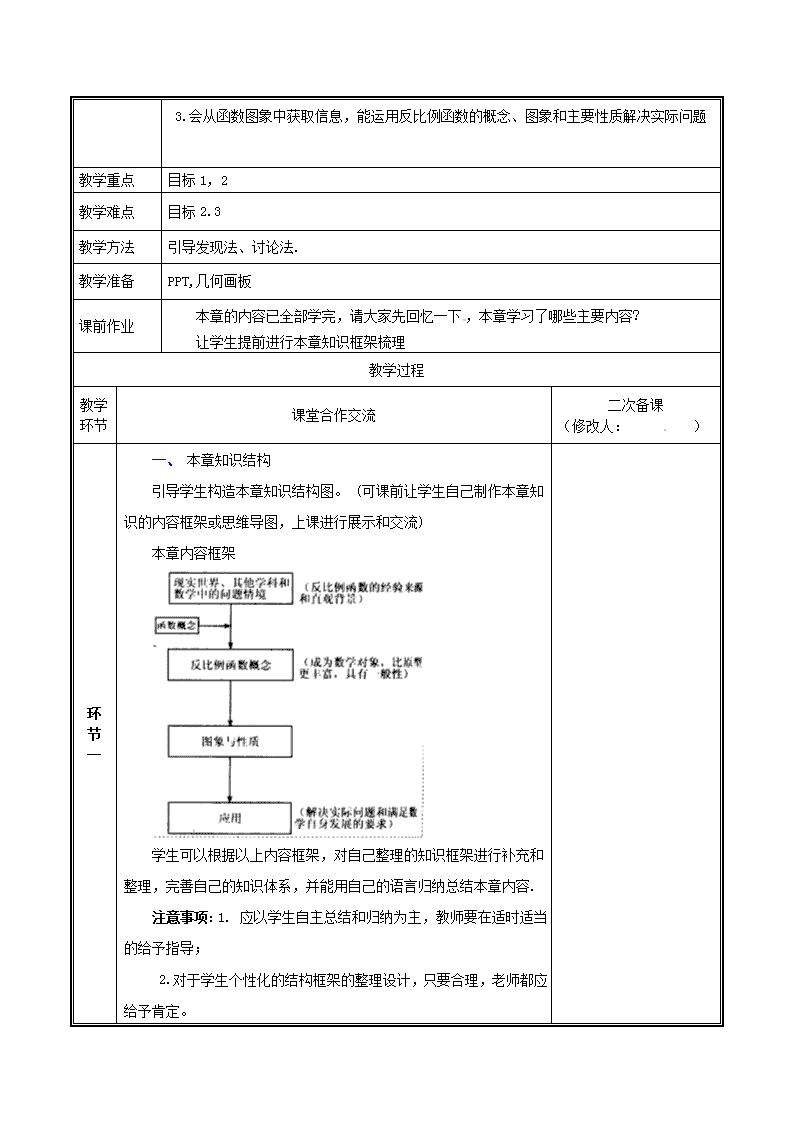
反比例函数的应用 课 题 反比例函数的应用 课时安排 共(1 )课时 课程标准 课标P34 结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数的表达式;能画出反比例函数的图像,根据图像和表达式探索理解k>0和k<0时,图像的变化情况;能用反比例函数解决简单的实际问题。 学习目标 1.经历抽象反比例函数概念的过程,理解反比例函数的概念. 2.会作反比例函数的图象,并探索和掌握反比例函数的主要性质. 3.会从函数图象中获取信息,能运用反比例函数的概念、图象和主要性质解决实际问题 教学重点 目标1,2 教学难点 目标2.3 教学方法 引导发现法、讨论法. 教学准备 PPT,几何画板 课前作业 本章的内容已全部学完,请大家先回忆一下,本章学习了哪些主要内容? 让学生提前进行本章知识框架梳理 教学过程 教学环节 课堂合作交流 二次备课 (修改人: ) 环 节 一 一、 本章知识结构 引导学生构造本章知识结构图。 (可课前让学生自己制作本章知识的内容框架或思维导图,上课进行展示和交流) 本章内容框架 学生可以根据以上内容框架,对自己整理的知识框架进行补充和整理,完善自己的知识体系,并能用自己的语言归纳总结本章内容. 注意事项:1. 应以学生自主总结和归纳为主,教师要在适时适当的给予指导; 2.对于学生个性化的结构框架的整理设计,只要合理,老师都应给予肯定。 (二) 举出现实生活中有关反比例函数的实例,并归纳出反比例函数概念. 课中作业 完善整理知识框架 环 节 二 二、实际运用 例一 1.下列函数中,其图象位于第一、三象限的有哪些?在其图象所在象限内,y的值随x值的增大而增大的是哪些 ( ) (1)y= (3)y= (2)y= (4)y=- 2.在函数y=的图象上任取一点P,过P分别作x轴、y轴的平行线,与坐标轴围成的矩形面积是多少? 例二 1.一个圆台物体的上底面积是下底面积的,当下底面放在桌子上时,对桌面的压强是200 Pa,倒过来放,对桌面的压强是多少? 2.一定质量的CO2,当体积v=5米3时.它的密度ρ=1.98千克/米3,求(1)ρ与v的函数关系式;(2)当v=9米3时,CO2的密度. 课中作业 1.对于函数y=,当x>0时,y_______0,这部分图象在第______象限;对于y=-,当x<0时,y____0,这部分图象在第_____象限. 2.函数y=的图象在第____象限内,在每一个象限内,y随x的增大而______. 3.根据下列条件,分别确定函数y=的表达式 (1)当x=2时,y=-3; (2)点(-)在双曲线y=上. (5)已知排水管的最大排水量为每时12,那么最少多长时间可将满池水全部排空?(课本P149) 环 节 三 三、拓展提升 如图,一次函数与反比例函数的图象交于点和,与y轴交于点C. (1)= ,= ; (2)根据函数图象可知,当>时,x的取值范围是 ; (3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当:=3:1时,求点P的坐标. 二、 感悟收获,师生小结 教师引导学生进行回顾和整理,然后通过师生交流和生生交流,回答以下问题:本节课我们都一起回顾和复习了哪些内容? 交流预设: 1. 反比例函数概念 2. 反比例函数图像的做法及性质 3. 反比例函数在生活中的应用 4. 做题时要注意数形结合 5. 具体题目的解题思路 课中作业 课本P162 总复习 11题 课后作业设计: 《全品学练考》作业手册 第六章总复习 (修改人: ) 板书设计: 反比例函数复习 例题(格式规范) 教学反思: 本节课采用引导、启发及问题讨论相结合的教学方式,引导学生从已有的知识和生活经验出发,师生共同探究解决新问题的途径和方法。这一过程中,充分发挥教师的主导作用,学生的主体作用,教材的主源作用,旧知识的迁移作用,学生之间的相互作用,从而师生得到共同发展。查看更多