- 2023-07-08 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级下册数学教案29-2 第3课时 由三视图确定几何体的面积或体积 人教版
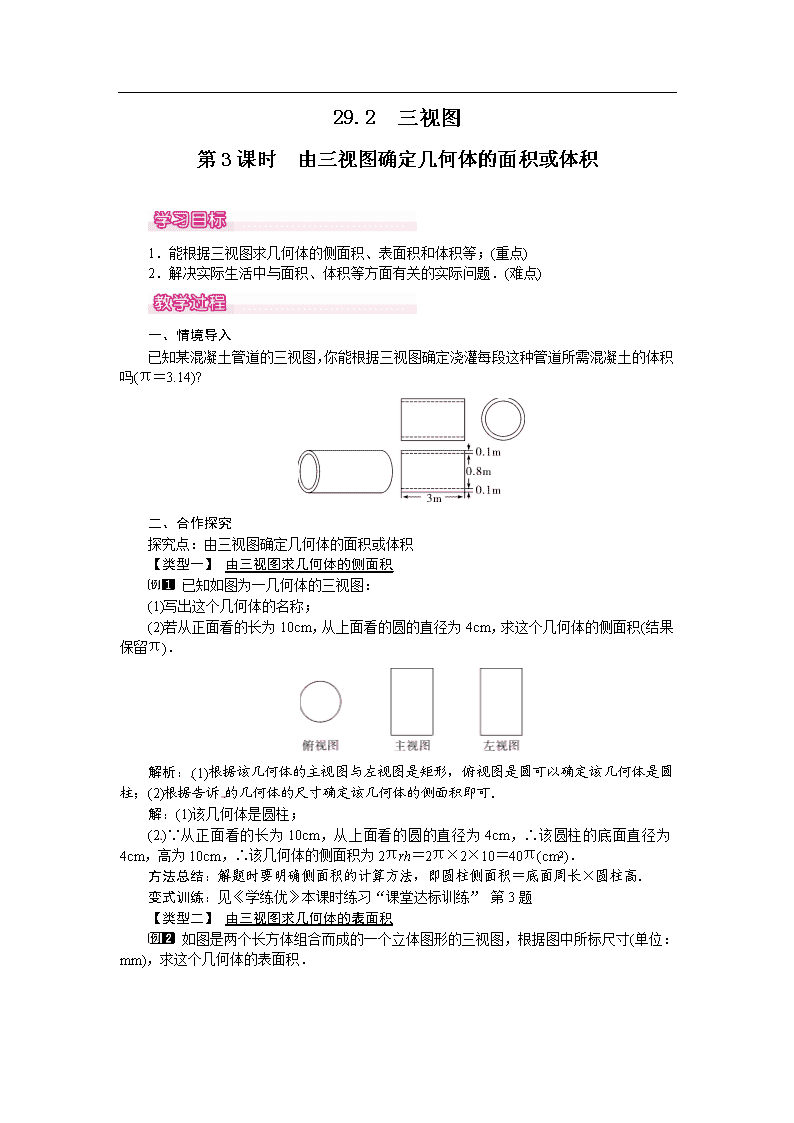
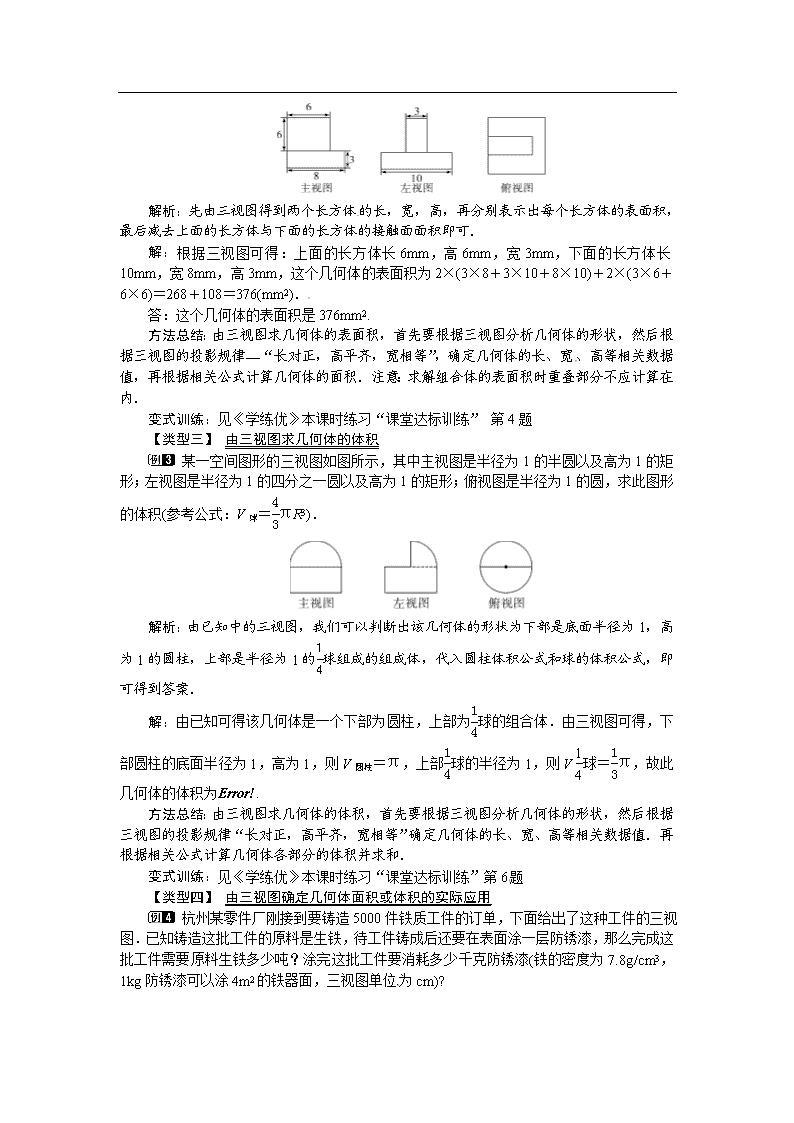
29.2 三视图 第3课时 由三视图确定几何体的面积或体积 1.能根据三视图求几何体的侧面积、表面积和体积等;(重点)[来源:学科网ZXXK] 2.解决实际生活中与面积、体积等方面有关的实际问题.(难点) [来源:学科网][来源:学科网] 一、情境导入 已知某混凝土管道的三视图,你能根据三视图确定浇灌每段这种管道所需混凝土的体积吗(π=3.14)? 二、合作探究 探究点:由三视图确定几何体的面积或体积 【类型一】 由三视图求几何体的侧面积 已知如图为一几何体的三视图: (1)写出这个几何体的名称; (2)若从正面看的长为10cm,从上面看的圆的直径为4cm,求这个几何体的侧面积(结果保留π). 解析:(1)根据该几何体的主视图与左视图是矩形,俯视图是圆可以确定该几何体是圆柱;(2)根据告诉的几何体的尺寸确定该几何体的侧面积即可. 解:(1)该几何体是圆柱; (2)∵从正面看的长为10cm,从上面看的圆的直径为4cm,∴该圆柱的底面直径为4cm,高为10cm,∴该几何体的侧面积为2πrh=2π×2×10=40π(cm2).[来源:Z_xx_k.Com] 方法总结:解题时要明确侧面积的计算方法,即圆柱侧面积=底面周长×圆柱高. 变式训练:见《学练优》本课时练习“课堂达标训练” 第3题 【类型二】 由三视图求几何体的表面积[来源:学科网ZXXK] 如图是两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个几何体的表面积. 解析:先由三视图得到两个长方体的长,宽,高,再分别表示出每个长方体的表面积,最后减去上面的长方体与下面的长方体的接触面面积即可. 解:根据三视图可得:上面的长方体长6mm,高6mm,宽3mm,下面的长方体长10mm,宽8mm,高3mm,这个几何体的表面积为2×(3×8+3×10+8×10)+2×(3×6+6×6)=268+108=376(mm2). 答:这个几何体的表面积是376mm2. 方法总结:由三视图求几何体的表面积,首先要根据三视图分析几何体的形状,然后根据三视图的投影规律—“长对正,高平齐,宽相等”,确定几何体的长、宽、高等相关数据值,再根据相关公式计算几何体的面积.注意:求解组合体的表面积时重叠部分不应计算在内. 变式训练:见《学练优》本课时练习“课堂达标训练” 第4题 【类型三】 由三视图求几何体的体积 某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为1的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积(参考公式:V球=πR3). 解析:由已知中的三视图,我们可以判断出该几何体的形状为下部是底面半径为1,高为1的圆柱,上部是半径为1的球组成的组成体,代入圆柱体积公式和球的体积公式,即可得到答案. 解:由已知可得该几何体是一个下部为圆柱,上部为球的组合体.由三视图可得,下部圆柱的底面半径为1,高为1,则V圆柱=π,上部球的半径为1,则V球=π,故此几何体的体积为. 方法总结:由三视图求几何体的体积,首先要根据三视图分析几何体的形状,然后根据三视图的投影规律“长对正,高平齐,宽相等”确定几何体的长、宽、高等相关数据值.再根据相关公式计算几何体各部分的体积并求和. 变式训练:见《学练优》本课时练习“课堂达标训练”第6题 【类型四】 由三视图确定几何体面积或体积的实际应用 杭州某零件厂刚接到要铸造5000件铁质工件的订单,下面给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗多少千克防锈漆(铁的密度为7.8g/cm3,1kg防锈漆可以涂4m2的铁器面,三视图单位为cm)? 解析:从主视图和左视图可以看出这个几何体是由前后两部分组成的,呈一个T字形状.故可以把该几何体看成两个长方体来计算. 解:∵工件的体积为(30×10+10×10)×20=8000cm3,∴重量为8000×7.8=62400(g)=62.4(kg),∴铸造5000件工件需生铁5000×62.4=312000(kg)=312(t).∵一件工件的表面积为2×(30×20+20×20+10×30+10×10)=2800cm2=0.28m2.∴涂完全部工件需防锈漆5000×0.28÷4=350(kg). 方法总结:本题主要考查了由三视图确定几何体和求几何体的面积;关键是得到几何体的形状,得到所求的等量关系的相对应的值. 变式训练:见《学练优》本课时练习“课后巩固提升”第7题 三、板书设计 1.由三视图求几何体的侧面积; 2.由三视图求几何体的表面积; 3.由三视图求几何体的体积. 本节重在引导学生总结解决此类问题的方法和规律,探究其实质.在小组讨论的过程中,学生了解了三视图中相关数据的对应关系,即“长对正,高平齐,宽相等”,找到了解决问题的根本,通过具体的例题,让学生进行练习,巩固学习效果.查看更多